线段树分裂

线段树分裂

顾名思义，就是把一颗线段树按照排名分成两棵树，通常会和线段树合并拌着吃。用官方一点的话来说，线段树分裂是线段树合并的逆运算，一般用于线段树维护的可重集，可以把一个可重集按照大小拆分成两个子集分别维护
注意当分裂和合并都存在时，我们在合并的时候必须回收节点，以避免分裂时会可能出现节点重复占用的问题

如何实现

想一想还学过什么数据结构依靠分裂和合并维护自身的值？
FHQ Treap !
没错，所以线段树合并与分裂一定程度上与FHQ Treap中的分裂合并操作比较相似
观察下面的分裂过程：



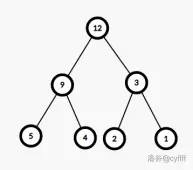
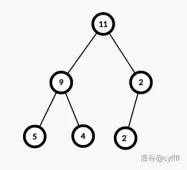
最左边的线段树即可按\([1,3]\)和\([4,4]\)分裂成右边两颗线段树
考虑一个\(split\)函数，传入参数\(p,q,L,R\)，代表把p上\([L,R]\)这一段区间分裂出来放到q上。首先我们容易知道，如果\(p=0\)也就是要分裂的节点是空节点，那啥也不用分了直接返回0。考虑用\(l,r\)维护当前递归到的区间，如果当前区间被目标区间完全包含，则直接把q赋值为p并清空p表示已经转移成功。如果目标区间不完全包含当前区间，就继续递归左右子树，进行分裂操作。简单来说，就是这么三步：
从 1 号结点开始递归分裂，当节点不存在或者代表的区间 [s,t] 与 [l,r] 没有交集时直接回溯
当 [s,t] 与 [l,r] 有交集时需要开一个新结点
当 [s,t] 包含于 [l,r] 时，需要将当前结点直接接到新的树下面，并把旧边断开

例题

P5494【模板】线段树分裂
五个操作，\(op_{0}\)把\([x,y]\)分裂出来，直接\(split\)即可；\(op_{1}\)单次合并；\(op_{2}\)插入x个p单点修改即可，因为维护的是权值线段树；\(op_{3}\)求\([x,y]\)中的数的个数，在权值线段树上区间求和；\(op_{4}\)查询区间第k大
代码：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define N 200010

int n,m;
int base[N*50];//初始新建的可重集中数字i的个数 
struct segtree{//动态开点权值线段树 
	int val,son[2];
}t[N*50];
int op,p,x,y;
int root[N*4];//存储根 
int rub[N*50];//回收站，存储被删除的点 
int cnt,tot;//cnt存储被删除节点的总数，tot存储新建节点的总数
int idx=1;//当前访问的根
 
/*内存分配与回收*/
//同时出现线段树分裂与合并时，需要进行节点的分配与回收，避免复用和冗余
int New(){
	//回收站里有点就复用，否则新建 
	return (cnt?rub[cnt--]:++tot);
} 

void del(int &p){
	//清空后放入回收站等待复用，并将被删结点和其父亲之间的关系解除 
	t[p].son[0]=t[p].son[1]=t[p].val=0;
	rub[++cnt]=p;
	p=0;
}

void push_up(int p){
	t[p].val=t[t[p].son[0]].val+t[t[p].son[1]].val;
}

/*建树*/
void build(int &p,int l,int r){
	if(!p) p=New();//没有就申请新内存
	if(l==r){
		cin>>t[p].val;//输入叶子节点权值 
		return;
		//叶子节点只记录这个数本身，其val代表这个数的出现次数 
	} 
	int mid=(l+r)>>1;
	build(t[p].son[0],l,mid);
	build(t[p].son[1],mid+1,r);
	push_up(p);
	return;
}

/*单点修改*/
//加入k个数x，相当于把点x的权值增加k 
void modify(int &p,int l,int r,int x,int k){
	if(!p) p=New();//如果没有就新建
	if(l==r){//找到x本身，直接更改 
		t[p].val+=k;
		return; 
	} 
	int mid=(l+r)>>1;
	//按照大小判断x属于左子树还是右子树，往对应方向寻找 
	if(x<=mid) modify(t[p].son[0],l,mid,x,k);
	else modify(t[p].son[1],mid+1,r,x,k);
	push_up(p);
	return;
}

/*线段树合并*/
//合并以p,q为根的两棵子树，并返回合并后的新根(此处将q并到p上) 
int merge(int p,int q,int l,int r){
	//if(!rt1&&!rt2) return 0;
	if(!p||!q) return p+q;
	if(l==r){
		t[p].val+=t[q].val;
		del(q);
		return p;
	}
	int mid=(l+r)>>1;
	t[p].son[0]=merge(t[p].son[0],t[q].son[0],l,mid);
	t[p].son[1]=merge(t[p].son[1],t[q].son[1],mid+1,r);
	push_up(p);
	del(q);
	return p;
}

/*线段树分裂*/
//把p包含的区间内，L到R的部分分裂到q代表的线段树中 
void split(int &p,int &q,int l,int r,int L,int R){
	if(R<l||r<L) return;//当前区间与目标区间没有交集，直接返回
	if(!p) return;//节点为空，无法分裂，返回 
	if(L<=l&&r<=R){
		//区间完全包含，直接赋值，然后把原线段树节点清空
		q=p;
		p=0;
		return; 
	}
	//如果目标节点为空，需要申请新节点
	if(!q) q=New();
	int mid=(l+r)>>1;
	//分别递归左右子树，进行分裂 
	if(l<=mid) split(t[p].son[0],t[q].son[0],l,mid,L,R);
	if(mid<r) split(t[p].son[1],t[q].son[1],mid+1,r,L,R); 
	//更新左右子树权值 
	push_up(p);
	push_up(q);
	return;
}

/*区间求和*/
//求区间l~r中大小处在L~R的有多少个数
int query(int p,int l,int r,int L,int R){ 
	if(!p) return 0;
	if(L<=l&&R>=r){
		return t[p].val;//完全包含直接返回 
	}
	int res=0; 
	int mid=(r+l)>>1;
	if(l<=mid) res+=query(t[p].son[0],l,mid,L,R);
	if(mid<r) res+=query(t[p].son[1],mid+1,r,L,R);
	return res;
} 

/*求区间第k大*/
int kth(int p,int l,int r,int k){
	if(l==r) return l;
	int mid=(l+r)>>1   ;
	int lft=t[t[p].son[0]].val;
	if(lft>=k) return kth(t[p].son[0],l,mid,k);
	else return kth(t[p].son[1],mid+1,r,k-lft);
}

signed main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	build(root[1],1,n);
	for(int i=1;i<=m;i++){
		cin>>op;
		if(op==0){//分裂操作 
			cin>>p>>x>>y;
			split(root[p],root[++idx],1,n,x,y);
		}else if(op==1){
			cin>>p>>x;
			root[p]=merge(root[p],root[x],1,n);
		}else if(op==2){
			cin>>p>>x>>y;
			modify(root[p],1,n,y,x);
		}else if(op==3){
			cin>>p>>x>>y;
			cout<<query(root[p],1,n,x,y)<<'\n';
		}else if(op==4){
			cin>>p>>x;
			if(t[root[p]].val<x) cout<<-1<<"\n";
			else cout<<kth(root[p],1,n,x)<<"\n";
		}
	}
	return 0;
}