网络流
网络流
网络流是一类特殊的有向图,其最大的特点是存在两个特殊的点:源点和汇点。源点只有出边,汇点只有入边,使得整个网络流图拥有了一个类似于河道的结构,也就是很多条并行的源点指向汇点的路径
对于一个网络\(E\),做出如下规定:
给E中的每条边都赋予一个权值w,称为每条边的容量
定义流为边集到自然数集或整数集的一个映射关系
定义每条边对应的流的数量为它的流量,规定每条边的流量不能超过其容量
对于网络中所有非源汇点的点,其入边流量总和等同于出边流量。这一性质称为流守恒性
定义一个边集\(G\),如果\(G\subseteq{E}\)且从\(E\)中删去\(G\)后,\(E\)不再连通,则称\(G\)是\(E\)的一个割。对于其中\(G\)的容量和最小的一个割,称为最小割
在任意时刻,网络中所有节点以及剩余容量大于0的边构成的子图被称为残量网络
常见的网络流问题包括以下几项:
最大流问题:对于网络\(E\),给每条边指定流量,得到合适的流\(f\),使得\(f\)的流量尽可能大。此时我们称\(f\)是\(E\)的最大流
最小割问题:对于网络v,找到合适的割\(G\),使得\(G\)的容量尽可能小。此时我们称\(G\)是\(E\)的最小割
最小费用最大流问题:在网络\(E\)上,对每条边给定一个权值cost,称为费用,含义是单位流量通过 (u, v) 所花费的代价。对于\(E\)所有可能的最大流,我们称其中总费用最小的一者为最小费用最大流
最大流问题
对于一个网络,合法的流函数有很多,其中使得整个网络流量之和最大的流函数称为网络的最大流,此时的流量和被称为网络的最大流量
最大流能解决许多实际问题,比如:一条完整运输道路(含多条管道)的一次最大运输流量,还有二分图等
下面就来介绍计算最大流的两种算法:EK增广路算法和Dinic算法
EK增广路算法
定义一条从源点指向汇点的路径,如果这条路径上的每条边都有剩余流量(没填满),称这条路为增广路
显然对于一条增广路,我们可以让一条新的流顺着它流过去,从而使网络的流量增大
EK算法的核心思想就是不断用BFS寻找增广路并不断更新最大流量值,直到网络上不存在增广路为止
在BFS寻找一条增广路时,我们只需要考虑剩余流量不为0的边,然后找到一条从S到T的路径,同时计算出路径上各边剩余容量值的最小值dis,则网络的最大流量就可以增加dis(经过的正向边容量值全部减去dis,反向边全部加上dis)
为了实现这个功能,我们需要引入一个新的概念————反向边
反向边
为什么要建反向边?
因为可能一条边可以被包含于多条增广路径,所以为了寻找所有的增广路经我们就要让这一条边有多次被选择的机会
而构建反向边则是这样一个机会,相当于给程序一个反悔的机会!
为什么是反悔?
因为我们在找到一个dis后,就会对每条边的容量进行减法操作,而直接更改值就会影响到之后寻找另外的增广路
当一条边的流量\(f(x,y)>0\)时,根据斜对称性质,它的反向边流量\(f(y,x)<0\),此时必定有\(f(y,x)<c(y,x)\),所以EK算法除了遍历原图的正向边以外还要考虑遍历每条反向边
反向边的作用可参考下图:

实现
建图时,采取相邻交替的方式建立正反双向边,也就是偶数编号为正向,奇数编号为反向,这样bfs时就可以通过x^1的方式快速访问反向边。其他就按照上文所说实现即可,见代码:
#include<bits/stdc++.h>
using namespace std;
#define N 500010
#define int long long
#define inf 2147483647
int n,m,s,t;
struct edge{
int to,nxt;
int flow;//流量
}e[N<<1];//建反向边开二倍空间
int head[N],tot=1;
int u,v,w;
int ans,dis[N];
int vis[N];
int pre[N];
int flag[3000][3000];
void add(int u,int v,int w){
e[++tot].to=v;
e[tot].flow=w;
e[tot].nxt=head[u];
head[u]=tot;
}
//寻找增广路
bool bfs(){
for(int i=1;i<=n;i++) vis[i]=0;//初始化vis数组
queue<int> q;
q.push(s);//源点入队
vis[s]=1;//标记源点
dis[s]=inf;//源点距离初始化为极大值
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=head[x];i;i=e[i].nxt){
if(e[i].flow==0) continue;
//流量剩余为0则不能通过,不考虑
int y=e[i].to;
if(vis[y]==1) continue;
//本条增广路被访问过,则忽略
dis[y]=min(dis[x],e[i].flow);
//更新最短距离
pre[y]=i;//记录前驱,便于修改边权
q.push(y);
vis[y]=1;//入队并标记
if(y==t) return 1;
//搜到汇点则说明成功找到一条路,返回1
}
}
return 0;//中途断掉,返回0
}
//更新所经过的正反向边的边权
void update(){
int x=t;
while(x!=s){//反向扫,更新
int y=pre[x];
//正向边减掉流量,代表已有流经过
e[y].flow-=dis[t];
//反向边加上流量,代表反悔,撤销流
e[y^1].flow+=dis[t];
x=e[y^1].to;//跳下一个
}
ans+=dis[t];//累加每一条增广路径的最小值
}
signed main(){
cin>>n>>m>>s>>t;
for(int i=1;i<=m;i++){
cin>>u>>v>>w;
if(!flag[u][v]){//去重边
add(u,v,w);
add(v,u,0);//反向边,权值初始为0
flag[u][v]=tot;//记录编号
}else{
e[flag[u][v]-1].flow+=w;
//重边直接累加边权
}
}
while(bfs()!=0){
update();
//重复执行bfs->update直到不存在增广路
}
cout<<ans;
return 0;
}
Dicnic算法
对于EK算法而言,他只能做到一次找到一条增广路。那么能不能一次找到多条增广路呢?答案就是Dicnic算法
在这里需要先引入分层图的概念
分层图
根据BFS宽度优先搜索,我们知道对于一个节点\(x\),我们用\(d[x]\)来表示它的层次,即S到x最少需要经过的边数。在残量网络中,满足\(d[y]=d[x]+1\)的边\((x,y)\)构成的子图被称为分层图(相信大家已经接触过了吧),而分层图很明显是一张有向无环图
我们可以使用BFS序创建出分层图,然后用DFS按层向下搜索。如果能从顶层搜到底层就说明搜到了一条流。所以在DFS中,从源点开始,每次我们向下一层次随便找一个点,直到到达汇点,然后再一层一层回溯回去,继续找这一层的另外的点再往下搜索,这样就满足了我们同时求出多条增广路的需求
所以,我们得到Dinic算法框架:
在残量网络上BFS求出节点的层次,构造分层图
在分层图上DFS寻找增广路,在回溯时同时更新边权
相较于EK算法,显然Dinic算法的效率更优也更快:虽然在稀疏图中区别不明显,但在稠密图中Dinic的优势便凸显出来了(所以Dinic算法用的更多)
Dicnic算法的时间效率还能进行优化
当前弧优化
当前弧优化
对于一个节点\(x\),当它在DFS中走到了第i条弧时,前i−1条弧到汇点的流一定已经被流满而没有可行的路线了
那么当下一次再访问\(x\)节点时,前i−1条弧就没有任何意义了
所以我们可以在每次枚举节点\(x\)所连的弧时,改变枚举的起点,这样就可以删除起点以前的所有弧,来达到优化剪枝的效果
对应到代码中,就是\(pre\)数组,见代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 2147483647
#define N 500010
int n,m,s,t;
int u,v,w;
int ans,dep[N];//dep为层次
struct edge{
int to,nxt,flow;
}e[N];
int head[N],tot=1;
int pre[N];//用于当前弧优化,记录每个节点当前遍历到的边的编号
void add(int u,int v,int w){
e[++tot].to=v;
e[tot].flow=w;
e[tot].nxt=head[u];
head[u]=tot;
}
//在残量网络中构造分层图
bool bfs(){
for(int i=1;i<=n;i++) dep[i]=inf;//初始化所有节点的层次为无穷大
queue<int> q;
q.push(s);
dep[s]=0;//初始化所有节点的层次为无穷大
pre[s]=head[s];//初始化源点的当前弧为其第一条边
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=head[x];i;i=e[i].nxt){
//如果边的剩余容量大于0且该节点还未被访问过
int y=e[i].to;
if(e[i].flow>0&&dep[y]==inf){
q.push(y);
pre[y]=head[y];
dep[y]=dep[x]+1;//该节点的层次为其父节点的层次+1
if(y==t) return 1;
//如果到达了汇点,说明找到了一条增广路径,返回1
}
}
}
return 0;
}
//在分层图中寻找增广路径
inline int dfs(int x,int sum){
if(x==t) return sum;
int k,res=0;//子节点的增广流量;经过当前节点的总增广流
//从当前节点的当前弧开始遍历
for(int i=pre[x];i&∑i=e[i].nxt){
pre[x]=i;//当前弧优化
int y=e[i].to;
if(e[i].flow>0&&(dep[y]==dep[x]+1)){
k=dfs(y,min(sum,e[i].flow));
//如果该边无法增广,将该节点的层次设为无穷大,避免再次遍历
if(k==0) dep[y]=inf;
e[i].flow-=k;//剪枝,去掉增广完毕的点
e[i^1].flow+=k;
res+=k;//res表示经过某点的流量和
sum-=k;//sum表示经过该点的剩余流量
}
}
return res;
}
signed main(){
cin>>n>>m>>s>>t;
for(int i=1;i<=m;i++){
cin>>u>>v>>w;
add(u,v,w);
add(v,u,0);
}
//不断在残量网络中构造分层图并寻找增广路径,直到找不到为止
while(bfs()){
ans+=dfs(s,inf);
}
cout<<ans;
return 0;
}
最小割问题
在这里有一个极其重要的定理:最大流最小割定理
对于任意网络\(G\),其上的最大流\(f\)和最小割\(\{S, T\}\)总是满足\(|f| = ||S, T||\)
也就是指最小割和最大流可以相互转化
具体证明可以看oiwiki
根据这一理论,容易得到以下代码:
点击查看代码
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
constexpr int N = 1e4 + 5, M = 2e5 + 5;
int n, m, s, t, tot = 1, lnk[N], ter[M], nxt[M], val[M], dep[N], cur[N];
void add(int u, int v, int w) {
ter[++tot] = v, nxt[tot] = lnk[u], lnk[u] = tot, val[tot] = w;
}
void addedge(int u, int v, int w) { add(u, v, w), add(v, u, 0); }
int bfs(int s, int t) {
memset(dep, 0, sizeof(dep));
memcpy(cur, lnk, sizeof(lnk));
std::queue<int> q;
q.push(s), dep[s] = 1;
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = lnk[u]; i; i = nxt[i]) {
int v = ter[i];
if (val[i] && !dep[v]) q.push(v), dep[v] = dep[u] + 1;
}
}
return dep[t];
}
int dfs(int u, int t, int flow) {
if (u == t) return flow;
int ans = 0;
for (int &i = cur[u]; i && ans < flow; i = nxt[i]) {
int v = ter[i];
if (val[i] && dep[v] == dep[u] + 1) {
int x = dfs(v, t, std::min(val[i], flow - ans));
if (x) val[i] -= x, val[i ^ 1] += x, ans += x;
}
}
if (ans < flow) dep[u] = -1;
return ans;
}
int dinic(int s, int t) {
int ans = 0;
while (bfs(s, t)) {
int x;
while ((x = dfs(s, t, 1 << 30))) ans += x;
}
return ans;
}
int main() {
scanf("%d%d%d%d", &n, &m, &s, &t);
while (m--) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
addedge(u, v, w);
}
printf("%d\n", dinic(s, t));
return 0;
}
而对于最小割相关问题,需要注意一种特殊的题型:
平面图最小割问题
首先要知道什么是平面图
平面图:能画在平面上,满足除顶点处以外无边相交的图称为平面图。
网格图:形成一个网格的平面图称为网格图。形式化地,对于点数为\(n\times{m}\)的网格图,存在一种为每个点赋互不相同的标号\([i,j],(1\le{i}\le{n},1\le{j}\le{m})\)的方案,满足两点之间有边当且仅当它们的\(j\)相同且\(i\)相差\(1\),或\(i\)相同且\(j\)相差\(1\)
一般平面图最小割问题都在网格图上,所以我们先介绍网格图最小割,满足 边权非负 且 割的源点和汇点在边界 上。称一个点在边界上,当且仅当它的\(i=1,n\)或\(j=1,m\)

如上图,左边是一张平面图,右边是一张网格图,边界上所有点用黄色标注
考虑求网格图左上角\(s\)到右下角\(t\)的最小割,即一种划分点集的方式满足\(S\cup{T}=V\)且\(S\cap{T}=\emptyset\)并且\(s\in S,t\in T\),且两端分别在\(S,T\)的边(称为割边)的权值之和(称为割的权值)最小
考虑\(S\)和\(T\)的边界。这个边界对应了一条从右上到左下的路径。在两个相邻的面之间移动时,需要花费对应边权的代价,那么路径长度就对应了割的权值。如下图:
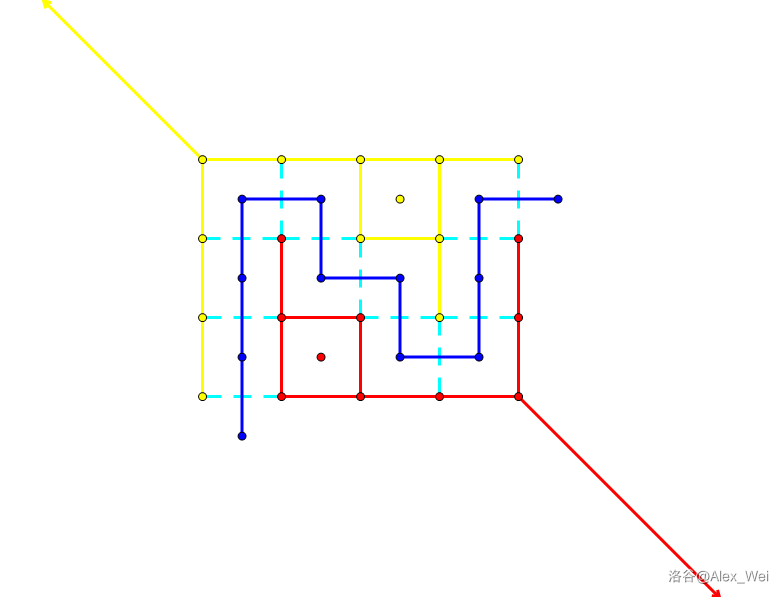
考虑从左上角和右下角向外引出两条权值无穷大的射线,将网格图外的平面分成左下和右上两部分。现在我们要建出网格图的对偶图:将所有面抽象成点,对于通过一条边相邻的两个面,在它们对应的点之间连权值为这条边的权值的边(这不是对偶图的严谨定义)
一个满足\(S\)连通,\(T\)连通的割,恰对应了对偶图上从右上无穷面代表的点到左下无穷面代表的点的路径,因此网格图最小割等于对偶图最短路,如下图:
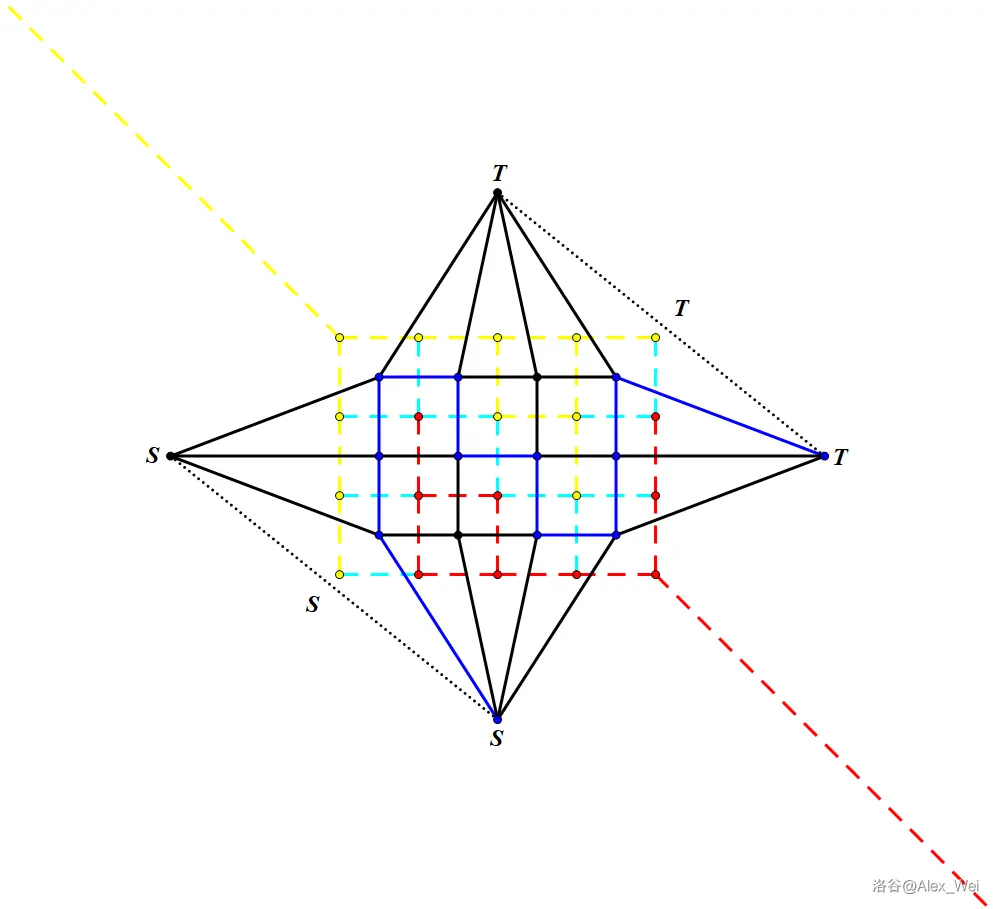
实边表示对偶图的边,虚边表示原图的边。注意左侧和下侧,上侧和右侧分别是同一个点。从右上到左下的最短路即为左上到右下的最小割。上图给出了一条可能的最短路以及它对应的最小割
扩展:不需要源汇在左上角和右下角。只要源汇在边界上,就可以通过转对偶图的方式求最小割。
扩展:不需要是网格图。平面图也可以转对偶图求最小割,整个过程没有用到网格图的性质,只是便于理解
费用流(最小费用最大流)
给定一个网络\(G\),对于网络的每条边,除了流量\(f\),还存在费用\(C\),要求最大化\(f(s,t)\)同时最小化\(c(s,t)\),称此时得到的结果为最小费用最大流
如何实现这一点呢?
SSP算法
考虑一种贪心的做法,每次跑最大流的时候都选择一条单位费用最小的增广路进行增广,直到我们跑不动为止
具体来说,就是用跑最短路代替原本的BFS
以下是对这种方法的证明:
我们考虑使用数学归纳法和反证法来证明 SSP 算法的正确性。
设流量为\(i\)的时候最小费用为\(f_{i}\)。我们假设最初的网络上 没有负圈,这种情况下 \(f_{0}=0\)。
假设用SSP算法求出的\(f_{i}\) 是最小费用,我们在\(f_{i}\)的基础上,找到一条最短的增广路,从而求出\(f_{i+1}\)。这时\(f_{i+1}-f_{i}\)是这条最短增广路的长度
假设存在更小的\(f_{i+1}\),设它为
\(f'_{i+1}\)。因为\(f_{i+1}-f_{i}\)已经是最短增广路了,所以
\(f'_{i+1}-f_{i}\)一定对应一个经过 至少一个负圈 的增广路
这时候矛盾就出现了:既然存在一条经过至少一个负圈的增广路,那么\(f_{i}\)就不是最小费用了。因为只要给这个负圈添加流量,就可以在不增加\(s\)流出的流量的前提下,使\(f_{i}\)对应的费用更小。
综上,SSP算法可以正确求出无负圈网络的最小费用最大流
代码实现也比较简单,就是把BFS等效替换为SPFA,为图添加cost代表费用,和最大流同时维护就行。注意反边的费用需要取反,也就是变成负数
基于EK算法的代码实现:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define N 500010
#define inf 2147483647
int n,m,s,t;
struct edge{
int to,nxt;
int flow;//流量
int cost;//费用
}e[2*N];
int head[N],tot=1;//tot设为1方便交替加边
int u,v,w,c;
int ansd,dis[N];//最大流答案;每条增广路的最小长度
int cst[N];//费用累加,用来跑最短路
int ansc;//最小费用
int vis[N];
int pre[N];//前驱
int flag[3000][3000];//记录边的序号
void add(int u,int v,int w,int c){
e[++tot].to=v;
e[tot].flow=w;
e[tot].cost=c;
e[tot].nxt=head[u];
head[u]=tot;
}
//寻找费用最小的增广路
bool spfa(){
for(int i=0;i<=n+1;i++) cst[i]=inf;//初始将cst数组设为极大值,跑最短路
queue<int> q;
q.push(s);//源点入队
vis[s]=1;
dis[s]=inf;
dis[t]=0;
cst[s]=0;//源点无需付费
while(!q.empty()){
int x=q.front();
q.pop();
vis[x]=0;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].to,fl=e[i].flow,ct=e[i].cost;
if(fl&&cst[y]>cst[x]+ct){
//流量不为0说明当前路可走,后一个条件更新最短路
cst[y]=cst[x]+ct;
dis[y]=min(dis[x],fl);
pre[y]=i;//记录前驱
if(!vis[y]){
q.push(y);
vis[y]=1;//新节点入队
}
}
}
}
return dis[t];//判断是否找到了一条增广路
}
//更新所经过的正反向边的边权
void update(){
int x=t;
while(x!=s){//反向扫,更新
int y=pre[x];
//正向边减掉流量,代表已有流经过
e[y].flow-=dis[t];
//反向边加上流量,代表反悔,撤销流
e[y^1].flow+=dis[t];
//最小流量增加:当前费用*全路流量,也就是流经这个点的费用
ansc+=dis[t]*e[y].cost;
x=e[y^1].to;//跳下一个
}
ansd+=dis[t];//累加每一条增广路径的最小值
}
signed main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m>>s>>t;
for(int i=1;i<=m;i++){
cin>>u>>v>>w>>c;
add(u,v,w,c);
add(v,u,0,-c);//反向边,权值初始为0
}
while(spfa()!=0){
update();
//重复执行spfa->update直到不存在增广路
}
cout<<ansd<<" "<<ansc;
return 0;
}
基于Dinic算法的代码实现
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define N 500010
#define inf 2147483647
int n,m,s,t;
int u,v,w,c;
struct edge{
int to,nxt,flow,cost;
}e[N*2];
int head[N],tot=1;
int ansd,ansc,cst[N];//意义和EK+SSP中的意义相同
int dep[N];//层次
int vis[N];//是否入队
int pre[N];//记录前驱,用于当前弧优化
void add(int u,int v,int w,int c){
e[++tot].to=v;
e[tot].flow=w;
e[tot].cost=c;
e[tot].nxt=head[u];
head[u]=tot;
}
//跑最短路的同时在残量网络中构建分层图
bool spfa(){
for(int i=1;i<=n;i++){
dep[i]=inf;
vis[i]=0;
cst[i]=inf;
}
queue<int> q;
q.push(s);
vis[s]=1;
dep[s]=0;//源点位于第0层
cst[s]=0;//源点不计费
pre[s]=head[s];//记录源点当前弧
while(!q.empty()){
int x=q.front();
q.pop();
vis[x]=0;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].to,fl=e[i].flow,ct=e[i].cost;
if(fl>0&&cst[y]>cst[x]+ct){
cst[y]=cst[x]+ct;
dep[y]=dep[x]+1;//分层
pre[y]=head[y];//记录当前弧
if(!vis[y]){//没被访问过
q.push(y);
vis[y]=1;
}
}
}
}
return cst[t]!=inf;//判断是否修改到了汇点
}
int dfs(int x,int sum){
if(x==t){
return sum;
}
int k,res=0;//子节点的增广流量;经过当前节点的总增广流量
vis[x]=1;
//从当前节点的当前弧开始遍历
for(int i=pre[x];i&∑i=e[i].nxt){
pre[x]=i;//当前弧优化
int y=e[i].to,fl=e[i].flow,ct=e[i].cost;
if(!vis[y]&&fl>0&&(dep[y]==dep[x]+1)&&cst[y]==cst[x]+ct){
k=dfs(y,min(sum,fl));
//如果该边无法增广,将该节点的层次设为无穷大,避免再次遍历
if(k==0) dep[y]=inf;
e[i].flow-=k;//剪枝,去掉增广完毕的点
e[i^1].flow+=k;
res+=k;//res表示经过某点的流量和
sum-=k;//sum表示经过该点的剩余流量
}
}
vis[x]=0;
return res;
}
signed main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m>>s>>t;
for(int i=1;i<=m;i++){
cin>>u>>v>>w>>c;
add(u,v,w,c);
add(v,u,0,-c);
}
//不断在残量网络中构造分层图并寻找增广路径,直到找不到为止
while(spfa()){
int tmp=dfs(s,inf);
ansd+=tmp;
ansc+=tmp*cst[t];
}
cout<<ansd<<" "<<ansc;
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号