根号分治

以一道题来说明何谓根号分治。

P3396 哈希冲突

如果对于每个操作进行暴力求解，即从 $y$ 开始不断累加 $x$。单次询问时间复杂度： $O(n)$，总时间复杂度 $O(nm)$。
可以预先处理好每个询问的结果，即用上一步的方法计算后将结果保存下来，用 $f[i][j] $ 表示模数为 $i$ 时，$j$ 池内的数字综合，询问时直接输出。预处理时间复杂度： $O(n^2)$，单次询问时间复杂度：$O(1)$，总时间复杂度：$O(n^2)$。
为什么前两种方法这么慢呢？因为询问拖慢了速度，即从 $y$ 开始累加 $x$，最多有可能累加 $n$ 次。
那么如何减少累加次数呢？
可以把我们的第1, 2步综合起来。分情况讨论一下：
5. 1. 如果询问的模数 $x > \sqrt n$ ，那么可以使用第一种方法暴力枚举，最多可能累加的次数为： $\sqrt n$ 次，所以单次询问最坏情况的时间复杂度为 $O(\sqrt n)$，如果进行 $m$ 次操作，则最坏时间复杂度为 $O(m \sqrt n)$。
5. 2. 如果询问的模数 $x \leq n$，那么可以使用第二种方法，先将所有结果存下来，共 $\sqrt n$ 种模数，共 $n$ 个数需要统计，预处理时间复杂度：$O(n \sqrt n)$，询问时间复杂度： $O(1)$，预处理 + 询问最坏时间复杂度为 $O(n \sqrt n)$。
因为 $n$ 和 $m$ 差不多，所以时间复杂度为 $O(n \sqrt n)$。
修改第 $x$ 的值为 $y$ 时，先对每一个模数下的 $x$ 进行处理，即 $f[x][x \% mod ] = f[x][x \% mod ] - a[x] + y$，时间复杂度：$O(\sqrt n)$，再对 $a[x]$ 进行处理，即 $a[x] = y$即可。

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 150010, S = 400;

int n, m, s;
int a[N];
int f[S][S];

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> n >> m;
	s = sqrt(n);
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= s; i++) {
	    for (int j = 1; j <= n; j++) {
	        f[i][j % i] += a[j];
	    }
	}
	char opt;
	int x, y;
	for (int i = 1; i <= m; i++) {
	    cin >> opt >> x >> y;
	    if (opt == 'A') {
	        if (x <= s) cout << f[x][y] << '\n';
	        else {
	            int ans = 0;
	            for (int j = y; j <= n; j += x) ans += a[j];
	            cout << ans << '\n';
	        }
	    }
	    else {
	        for (int j = 1; j <= s; j++) f[j][x % j]  = f[j][x % j] - a[x] + y;
	        a[x] = y;
	    }
	}
	return 0;
}

CF103D Time to Raid Cowavans

与上一题类似，对询问的左端点进行排序，处理到哪里就把前面的数字全删了。

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;
using i64 = long long;

const int N = 300010, S = 600;

int n, m, s;
int a[N];
i64 res[N];
i64 f[S][S];

struct query {
    int x, y, id;
}q[N];

bool cmp(const query a, const query b) {
    return a.x < b.x;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n;
    s = sqrt(n);
    for (int i = 1; i <= n; i++) cin >> a[i];
    cin >> m;
    for (int i = 1; i <= m; i++) {
        cin >> q[i].x >> q[i].y;
        q[i].id = i;
    }
    sort(q + 1, q + m + 1, cmp);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= s; j++) {
            f[j][i % j] += a[i];
        }
    }
    int last_position = 1;
    for (int i = 1; i <= m; i++) {
        int x = q[i].x, y = q[i].y, id = q[i].id;
        if (y <= s) {
            while (last_position < x) {
                for (int j = 1; j <= s; j++) {
                    f[j][last_position % j] -= a[last_position];
                }
                last_position++;
            }
            res[id] = f[y][x % y];
        }
        else {
            i64 ans = 0;
            for (int j = x; j <= n; j += y) ans += a[j];
            res[id] = ans;
        }
    }
    for (int i = 1; i <= m; i++) cout << res[i] << '\n';
    return 0;
}

CF1654E Arithmetic Operations

具体可见我写的题解。

以下内容与题解大致相同：

题目让我们求改变数字的最少次数，那我们转化一下，

求可以保留最多的数字个数 $cnt$，再用 $n$ 减一下就行，即 $res = n - cnt$。

我们先考虑两种暴力方法。

第一种暴力方法：

大体思路：因为要保留的最多，那么我们肯定要在众多等差数列中找能对应数字最多的那一个并保留下来。

首先，我们要知道一个概念。

对于这道题，那么我们可以暴力枚举公差 $d$（就是数组中相邻两项的差值都是 $d$，并把题目中的每个 $a[i]$ 对应的等差数列的最后一项 $a[i] + d \times (n - i)$ 计算出来。

对于同一个公差 $d$，如果不同位置计算出来的序列的最后一个值相同，那就说明它们属于同一个等差数列。

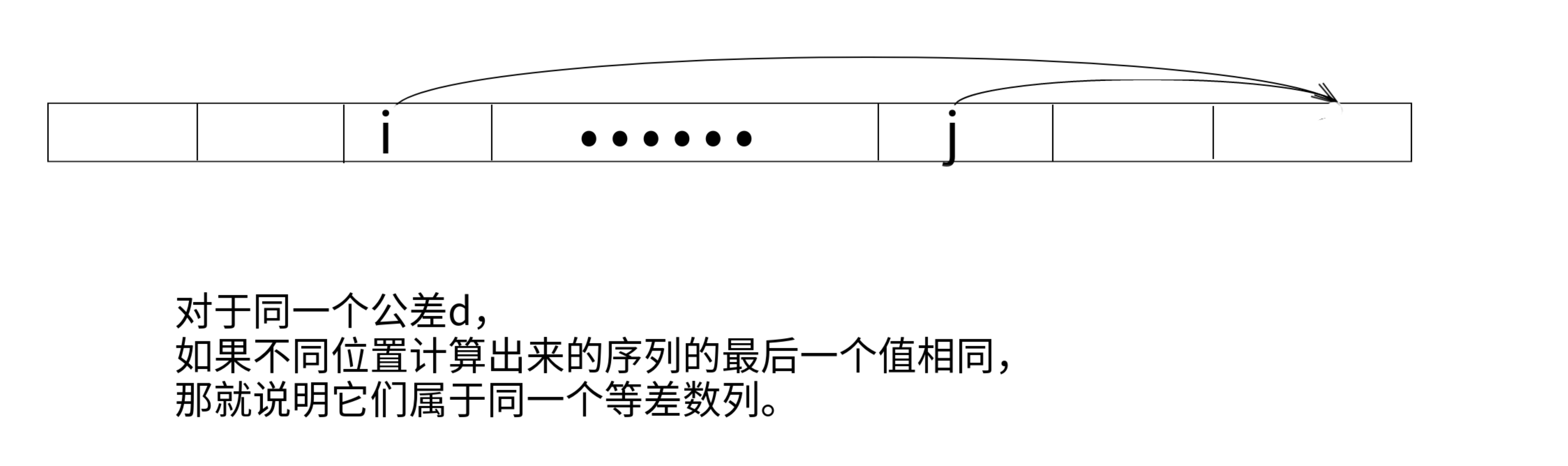
如果有 $x$ 个数字计算出来的最后一个值都相同，那么采用其对应的等差数列作为修改后的数组，这 $x$ 个数字是不需要改变的，只需要改变 $n - x$ 个数字。

那我们可以想到，用桶记录计算出来的值 $x$ 的出现次数 $a[x]$。如果某一次计算出来的值为 $x$，那么可以将 $a[x]$ 加 $1$。

如果 $a[x]$ 是 $a$ 中最大的元素，那么说明，以 $a[x]$ 为结尾的等差数列中存在的元素数量最多，那么更改数字的数量也就减少了，只需要 $n - a[x]$ 个元素。

这种方法的时间复杂度为 $O(DN)$，$D$ 为需要枚举的公差数量。

第二种暴力方法：

考虑动态规划，设 $f[i][j]$ 表示以 $a[i]$ 为等差数列最后一个元素的以 $j$ 为公差的等差数列最多可以保留的数字个数。

我们可以枚举上一个数字 $a[k]$，如果它与 $a[i]$ 在同一等差数列，那么有 $f[i][j] = f[k][j] + 1$，表示又可以多保存一个数字了。

那这个序列的公差是多少呢？

这样考虑，中间有 $i - k$ 个公差，差了 $a[i] - a[k]$，那么公差就是$\frac{a[i] - a[k]}{i - k}$。

如果除不尽怎么办呢，那么这就说明 $a[i]$ 和 $a[k]$ 不能在同一个等差数列，不然公差为小数！

那 $k$ 从哪里开始枚举呢？从 $1$ 开始是不是太慢了？

这个等会儿讲。

那么为了平衡这两种暴力算法，我们可以这样办：

取输入的数列 $a$ 的最大值 $m$。

我们只使用第一种方法枚举 $[0, \sqrt m]$ 的部分，时间复杂度为 $O(n \sqrt m)$。

我们使用第二种方法枚举 $[\sqrt m + 1, n]$ 的部分。

下面探讨第二种方法的时间复杂度，

首先回归到前面的问题，来探讨 $k$（$i$ 的上一位数字在哪里）从何处开始枚举，到哪里。

到哪里好解决，就是 $i - 1$。

而开始的地方，是 $i - \sqrt m$。为啥呢？

首先，因为公差 $D$ 在 $[\sqrt m + 1, n]$ 之间，所以 $D > \sqrt m$，那么我们计算差值 $a[i] - a[k] = (a[k] + (i - k) * D) - a[k] = (i - k) * D > (i - k) * \sqrt m$。

首先假设 $i, k$ 都在同一个等差数列中，如果 $k+ \sqrt m < i$，那么$a[i] - a[k] > (i - k) * \sqrt m > \sqrt m * \sqrt m = m$，这样的话，两数之差竟然比 $m$ 还要大，不成立，所以 $k + \sqrt m \geq i$，也就是说 $k$ 要从 $i - \sqrt m$ 开始枚举。

所以，第二种方法的时间复杂度为 $O(n \sqrt m)$。

那么这个题的时间复杂度就为 $O(n \sqrt m)$。

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <unordered_map>

using namespace std;

const int N = 100010;

int n;
int a[N], maxx, sqrtmaxx;

int u[(int)(N + N * sqrt(N))];                        // 第一种暴力方法的桶
unordered_map<int, int> f[N];                // 第二种暴力方法的动态规划数组。

int max_keep() {
    int ans = 0;
    for (int d = 0; d <= sqrtmaxx; d++) {    // 第一种暴力方法，枚举公差 D
        for (int i = 1; i <= n; i++) {
            ans = max(ans, ++u[a[i] + (n - i) * d]);
        }
        for (int i = 1; i <= n; i++) {
            u[a[i] + (n - i) * d]--;
	}
    }
    
    for (int i = 1; i <= n; i++) {                         // 第二种暴力方法，动态规划
        for (int j = max(1, i - sqrtmaxx); j < i; j++) {// j只用从 i - sqrt(m) 开始枚举
            if ((a[i] - a[j]) % (i - j) == 0) {
                int x = (a[i] - a[j]) / (i - j);
                if (x <= sqrtmaxx) continue;
                f[i][x] = max(f[i][x], f[j][x] + 1);
                ans = max(f[i][x] + 1, ans);
            }
        }
    }
    
    for (int i = 1; i <= n; i++) f[i].clear();    // 清空数组
    
    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i], maxx = max(maxx, a[i]);
    sqrtmaxx = sqrt(maxx);
    
    int ans1 = 0, ans2 = 0;
    ans1 = max_keep();
    reverse(a + 1, a + n + 1);                       // 应对公差为负数的情况
    ans2 = max_keep();
    
    cout << n - max(ans1, ans2) << '\n';
    return 0;
}

CF1580C Train Maintenance

我们以 $\sqrt m$ 为分界点来进行平衡。

设当前在进行第 $k$ 次操作，询问 $i$。

对于 $x[i] + y[i] \leq \sqrt m$,可以在 $last[x[i] + y[i]][day \mod (x[i] + y[i])]$ 上 $+1$，其中 $day$ 表示维修的时间，$k + x[i] \leq day \leq k + x[i] + y[i] - 1$，输出时暴力统计即可。

对于 $x[i] + y[i] > \sqrt m$ 的，可以在利用差分数组在 $f[day_1]$ 上 $+ 1$，在 $f[day_2]$ 上 $- 1$，其中 $day_1$ 表示所有的维修时间的开始时间，$day_2$ 表示所有维修时间的结束时间的后面一天。

时间复杂度： $O(m\sqrt m)$。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 200010, V = 450;

int n, m, s;
int st[N];
int f[N];
int last[V][V];
int x[N], y[N];

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	cin >> n >> m;
	s = sqrt(m);
	for (int i = 1; i <= n; i++) cin >> x[i] >> y[i];
	int opt, a;
	int sum = 0;
	for (int i = 1; i <= m; i++) {
		cin >> opt >> a;
		if (opt == 1) {
			if (x[a] + y[a] > s) {
				for (int j = i + x[a]; j <= m; j += x[a] + y[a]) {
					f[j] += 1;
					if (j + y[a] <= m) f[j + y[a]] -= 1;
				}
			}
			else {
				int b = i + x[a], e = i + x[a] + y[a] - 1;
				for (int j = b; j <= e; j++) {
					last[x[a] + y[a]][j % (x[a] + y[a])]++;
				}
			}
			st[a] = i;
		}
		else {
			if (x[a] + y[a] > s) {
				for (int j = st[a] + x[a]; j <= m; j += x[a] + y[a]) {
					f[j] -= 1;
					if (j < i) sum--;
					if (j + y[a] <= m) {
					    f[j + y[a]] += 1;
					    if (j + y[a] < i) sum++;
					}
				}
			}
			else {
				for (int j = st[a] + x[a]; j < st[a] + x[a] + y[a]; j++) {
					last[x[a] + y[a]][j % (x[a] + y[a])]--;
				}
			}
		}
		sum += f[i];
		int res = sum;
		for (int j = 1; j <= s; j++) res += last[j][i % j];
		cout << res << '\n';
	}
	return 0;
}

posted @ 2023-02-25 09:05 SunnyYuan 阅读(18) 评论(0) 收藏举报

刷新页面返回顶部

Loading

SunnyYuan的博客

根号分治

P3396 哈希冲突

CF103D Time to Raid Cowavans

CF1654E Arithmetic Operations

CF1580C Train Maintenance

公告