2021 OO 第一单元总结博客

一 基于度量的作业分析

Homework 1

● 总体思路

本次作业要求实现仅包含幂函数的简单多项式求导。由于作业要求比较简单，我仅构建了3个类（即Term项类，Polynomial表达式类和PolyFactory工厂类），各类之间无继承关系。

基本思路为，将输入读入后，利用正则表达式对该表达式中的项进行匹配，匹配成功后即进入工厂类创建一个项，得到该项的幂函数导数的指数与系数（即在创建的过程中就完成了同类项的合并）。我的UML类图如下：

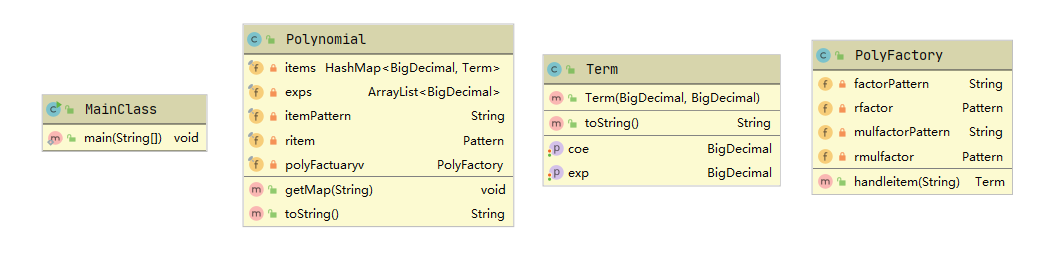
● 各类度量分析

本次作业总共创建了4个类，其中MainClass是主函数的入口，下面对其余3个类进行详细分析。

Polynomial类

该类为表达式类。其中包含5个属性与两个方法。该类代码共60行。

1. 属性

● items属性。该属性使用了hashmap容器，以指数为key值，一个项Term为value值，描述了该表达式包含了哪些项。

● exps属性。该属性使用了Arraylish容器，存放了所有项中出现在指数值，即items类中全部key值。该属性的存在方便了items的遍历输出。

● itemPattern和ritem属性。这两个属性为匹配项类的正则表达式和对正则表达式的预编译。将预编译放在类的属性中，避免了反复调用正则时，每一次都需预编译而浪费内存空间。

● polyFactuaryv属性。该属性为工厂类PolyFactory类的实例化。

2. 方法

● getMap方法。该方法实现了对某一表达式中各项的循环匹配，并将个项求导添加至items这一hashmap中。该方法代码共18行。

● toString()方法。该方法实现了对items类的遍历输出。该方法代码共23行。

Term类

该类为项类。共包含2个属性与2个方法。该类代码共51行。

1. 属性

● coe属性。该属性为大整数BigDecimal类型，为项的系数。

● exp属性。该属性为大整数BigDecimal类型，为幂函数的指数

2. 方法

● getMap方法。该方法实现了对某一表达式中各项的循环匹配，并将个项求导添加至items这一hashmap中。该方法代码共18行。

● toString()方法。该方法实现了对items类的遍历输出。该方法代码共23行。

PolyFactory类

该类为工厂类。共包含4个属性和一个方法。该类代码共51行。

1. 属性

● 该类中的四个属性均为正则表达式和对正则表达式的预编译。

2. 方法

● handleitem方法。该方法实现了在字符串中解析出一项，并获得该项导数的指数和系数的功能。该方法共38行。

各方法复杂度度量

作业中各方法复杂度度量如下：

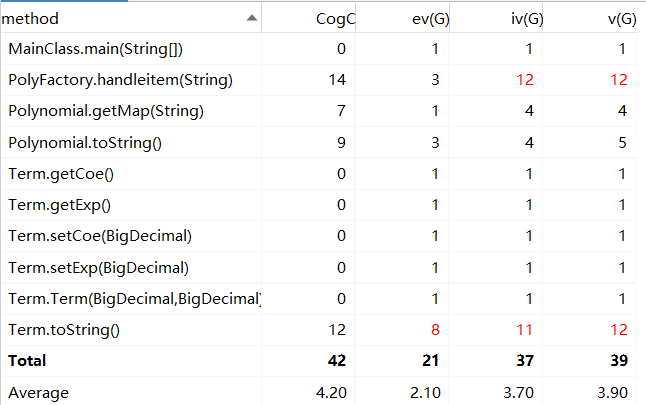
其中有两处方法复杂度飘红。PolyFactory工厂类中的handleitem方法飘红的原因为，该方法的分支数较多，需考虑不同的匹配情况并将项的指数和系数提取出来，导致复杂度较高。Term类中toString方法复杂度较高也是由于类似的原因，要讨论各种可能的输出组合并进行化简，使代码分支数较多，使得圈复杂度较高。

● 程序优缺点分析

程序优点

● 使用了工厂方法模式，设计模式合理。

● 利用hashmap容器的便利，对同类项进行了合并。

程序缺点

● 各类之间无继承关系。

● 可扩展性差。混淆了项与因子的概念。由于本次作业中只有常数因子和幂函数因子，我将这两种因子混为一谈，将常数因子理解为指数为0的特殊幂函数因子。又因为每项仅包含一种因子，我又将项和因子的概念混为一谈。而且我并没有实现单独的求导方法，而是直接在工厂中用了两行代码实现了对简单幂函数的求导，导致思路的混乱。

● 程序优化不够。未实现保证输出时第一项系数为正，以减少一个“+”的长度，也未将“x**2"优化为更短的”x*x"。

Homework 2

● 总体思路

本次作业在上次幂函数求导的基础上，加入了三角函数因子与表达式因子，使难度陡然增加。我认为本次作业是本单元作业中最难的一次。本次作业我创建了10个类，并使用了一层继承。

作业的基本思路为，将读入的表达式解析为一个个项，再将一个个项之间的因子解析出来，构建出一颗表达式树，再实现自底向上进行求导。由于项与项之间只能由加相连，因子与因子之间只能由乘相连，我并没有构建表示项之间关系的类。我的各类为表达式类、项类、各因子类（包括一个抽象银子和继承它的四种因子）、工厂类。其中，类图如下所示：

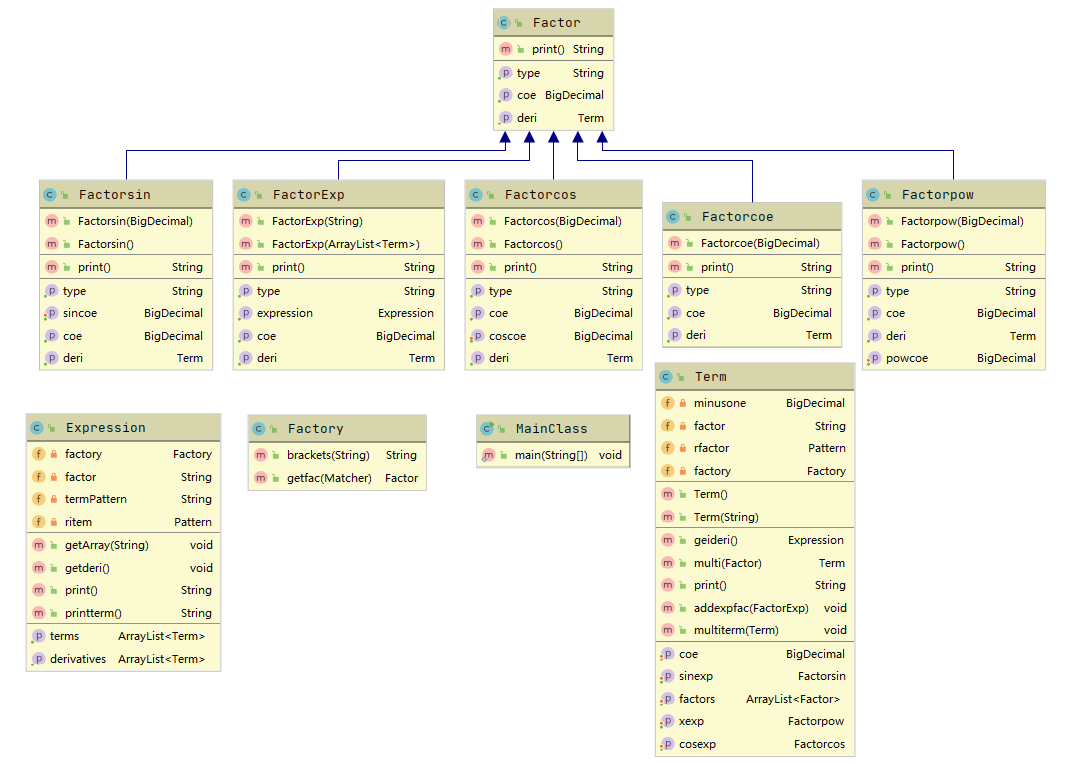
与第一次作业相比，第二次作业主要增加了各因子类、并实现了自底向上的求导。

● 各类度量分析

本次作业总共创建了10个类，其中MainClass是主函数的入口，下面在hw1的基础上，对其余9个类进行增量分析。

Expression类

该类相当于第一次作业中的Polynomial类，为表达式类。共有6个属性、4个方法，该类代码总长度为83行。

1. 属性

● factory属性、terms属性与hw1中功能相同，为工厂的实例化和表达式中项目的存储容器。在本次作业中，由于合并同类项比较困难，采用ArryaList存储各项，方便遍历。

● factor、termPattern与ritem为因子和项对应的正则表达式及其预编译。

● derivatives属性为新增属性，为ArrayList容器，存储求导得到的导函数的各项。

2. 方法

● getArray方法、print方法、printterm方法对应hw1的getmap方法和toString方法。

● getderi方法为新增方法，实现对表达式求导。其长度为7行。

Term类

该类相当于hw1中的Term类，为项类。但有较大改动，共有9个属性和7个方法。与hw1的将项与因子混淆不同，本次作业对这两者进行了严格区分。该类总长度243行，是最复杂的一个类。

1. 属性

● coe属性，为BigDecimal类型，代表项的系数。

● sinexp属性，为BigDecimal类型，代表项中sin(x)的指数。

● cosexp属性，为BigDecimal类型，代表项中cos(x)的指数。

● xexp属性，为BigDecimal类型，代表项中x的指数。

● factors属性，为ArrayList容器，储存所有表达式因子。

● 其余属性有minusone（负一，方便求导时减法使用）；factor、rfactor属性（正则表达式和对正则的预编译）；factory属性（工厂实例化）。

2. 方法

● Term()与Term(String)方法为Term类的构造方法，分别为7行和35行。

● getderi方法为对项的求导，返回一个表达式。该方法共55行。

● multi方法为因子相乘的方法，返回一个项类，实现对sin(x)、cos(x)和x指数的合并。该方法共26行。

● print方法类似于ToString方法，将该项以适当格式输出，该方法共35行。

● addexpfac方法用于化简，将只含有一项的表达式因子乘入项中。该方法共6行。

● multiterm方法用于项和项的相乘，该方法共8行。

Factory类

由于本次作业采用了工厂模式，工厂类由此应运而生。该类仅包含两个方法：

● brackets方法，用于对多层嵌套的括号进行标记。详细讲，即将首层嵌套的括号变为({}内容{})，而将第一层括号变为({@}内容{@})...随着层数增多不断增加@字符的个数。在正则匹配时，非贪婪匹配({}.*?{})，并将全部”{@"替换为“{”,从而达到处理括号的目的。该方法共26行。

● getfac方法，用于在匹配的各group结果中解析出各因子并调用各因子的构造方法。该方法共30行。

Factor抽象类

该抽象类用于被继承，为下面五个因子类提供了统一的4个方法接口，代码共22行：

● getType方法，返回因子的类型，如sin、cos等。

● getCoe方法，返回因子的指数。

● getDeri方法，返回因子的导数。

● print方法，将因子按规范格式输出。

由于下面各因子类仅完成了对抽象方法的具体化和自身的构造方法，为保证简洁性，以下仅阐述因子类中包含的属性。

Factorsin类

● sincoe属性，BigDecimal类型，为sin(x)的指数。

Factorcos类

● coscoe属性，BigDecimal类型，为cos(x)的指数。

FactorExp类

● expression属性，为Expression类的实例化，在此实现递归。

Factorcoe类

● coe属性，BigDecimal类型，为常数函数的常数。

Factorpow类

● powcoe属性，BigDecimal类型，为x的指数。

各类复杂度度量

本次作业中各类复杂度如下：

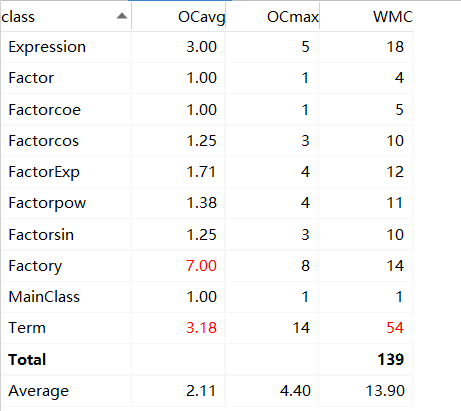
其中Factory和Term类复杂度较高。Factory类中getfac方法有较多分支，使复杂度较高。而Term类中getderi和print方法都有着较高的复杂度，使类平均复杂度较高。

● 程序优缺点分析

程序优点

● 本次作业的程序中使用了继承多态、初步具备了面向对象的编程思想，拥有了良好的扩展性。，大大减轻了第三次作业的负担。

​● 由于将sin(x)、cos(x)和幂函数列为Term类的3个单独属性，大大减少了合并同类项的痛苦。

​● 在优化时实现了对冗余括号的去除，减少了输出长度。

程序缺点

● 自己写了print函数而没有重写Object中的ToString方法，变成了一个十分奇怪的操作。

● 将sin(x)、cos(x)和幂函数列为Term类的3个单独属性，在对乘法进行求导时需要先进行3次分类讨论，稍稍给编程带来了麻烦。

Homework 3

● 总体思路

本次作业仍为实现简单多项式的求导，在第二次作业的基础上，允许sin类和cos类内嵌套因子，并要求实现对wrong format的判断。

本次作业我没有新增类，只在第二次作业的架构上做了微调。而判断wrong format时，使用了正则表达式匹配的方法，假定输入为正确的，寻找错误。当程序某处匹配失败时，即抛出异常，输出WF，终止程序的运行。

本次作业的类图如下所示：

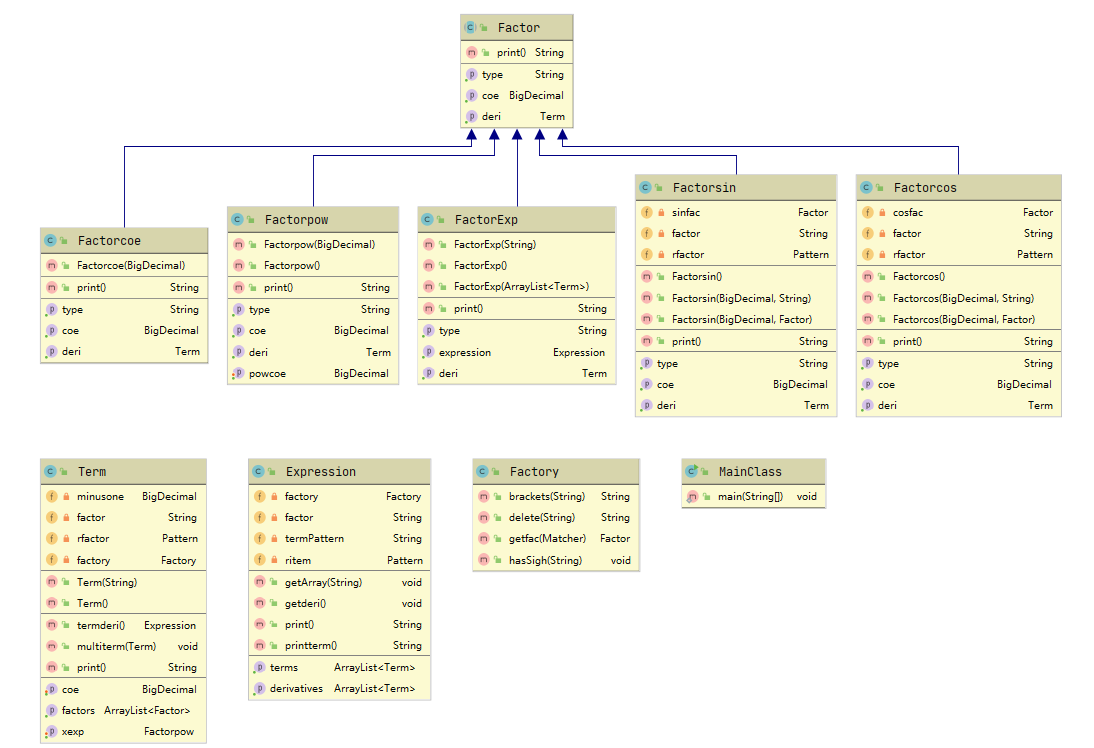
● 各类度量分析

hw3对于hw2来说，基本改动不大。所有的类及其功能完全一致。而对于属性和方法的改动主要为如下三处：

● 分别在Factorsin类与Factorcos类中增加了一个factor属性，为Factor类型，实现sin和cos对因子类的嵌套。

● 为实现对wf的判断，在正则表达式匹配的各处添加了mark标志，旨在实现头踩头、脚踩脚的匹配。

​● 扩展了工厂中的方法。增加了delete方法，实现对括号意外空白符的去除，为匹配提供了方便；增加了hasSign方法，实现了对项前符号的格式检查。

本次作业中各类复杂度如下：

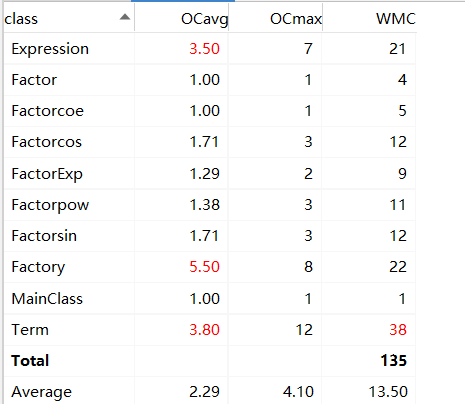
值得一提的是，起初我第三次作业的程序运行时间很长，在十层嵌套之后就会出现极为明显的卡顿。我经过debug分析后发现，是ToString方法被调用次数太多，导致程序复杂度高，CPU运行时间过长。为此，我对程序作出了如下改进：

● 在执行判断语句时，先将ToString函数的返回值赋给一String变量，再进行判断。

● 在Expression类和Term类中ToString长度较高的函数中，不再使用不可变变量String，而是使用可变变量StringBuilder，大大提高了程序的运行速度。也降低了程序的复杂度。

程序优缺点

程序优点

● 对ToString函数进行优化后，提高了运行速度，程序的执行效率有保障。

● 使用树形结构存储和求导，结构清晰。

程序缺点

● 在hw3中，我仍然没有更改我匹配输入的方法，仍使用很长的正则表达式来提取各部分的信息。在书写表达式类的正则表达式时，由于正则过长，其中出现了许多歧义，为WF的判断制造了很多麻烦。或许大部分同学使用的递归下降解析方法对于第三次作业更合适一些，但我仍然固守于自己的方法和结构，没有做出变通，没有努力掌握新方法。

● 没有利用hashcode和equals方法实现同类项合并，使程序性能略差，输出稍显冗长。

二 程序的bug

第三次作业的强测上我被爆出一类bug，即无法将sin(x)**1111111111111111这类输入判定为WF，但可以将sin(x)**52判定为WF。很显然，问题出在大整数的处理上，但我全程一直使用BigDecimal操作，没有使用过Int，到底是什么问题呢？

如下为我程序中Factorsin类里判断指数是否合法的代码：

int tempcoe = sincoe.intValue();
if (tempcoe > 50 || tempcoe < -50) {
	throw new RuntimeException();
} else {
    this.sinexp = sincoe;
}

只能说：凡有诡异bug，必有智障错误。我由于觉得CompareTo冗长，而且需要新建value为”50“和”-50“的BigDecimal类，就故作聪明地使用了intValue函数，用int类型比较了指数和±50的关系。修改为如下代码后即可：

if ((powcoe.compareTo(new BigDecimal("-50")) < 0) || powcoe.compareTo(new BigDecimal("50")) > 0) {
    throw new RuntimeException();
} else {
    this.powcoe = powcoe;
}

三 发现bug所采用的策略

我在发现bug时主要采用以下方式：

​● 形式建模验证。该方法主要适用于查找自己程序的bug。即按照逻辑顺序，一句一句通读自己的代码，而并不是按照类中书写的顺序。每次阅读大概会消耗1-2h，能非常有效地发现自己程序的笔误和逻辑不通的地方。通读之后，我会对自己的程序更为熟悉，此时可以寻找一个复杂度中等的样例，进行单步调试。随着不断调试到下一步，寻找程序潜在的思维漏洞，这种方法能帮助找到自己的思维死角，有效避免了形式建模带来的思维定势。只要沉得住气，形式建模往往是最有效的debug方式。可惜我hw3中测过得太晚了，没有完成对自己代码的形式建模验证，导致了无法弥补的后果。

● 利用简单的自动评测机。该方法适用于查找他人程序的bug。由于通读他人代码所消耗的时间较长，所以可以使用黑箱方法，利用自动测评机对其程序进行验证。我在和同学对拍的时候白嫖了他写的自动测评机（危），主要思想是在python中利用各随机函数不断嵌套，从随机生成因子并添加空格，到利用“*”组合为项，利用“+”组合为表达式，由此随机生成数据。再利用jar包得到标准输出，利用sympy库与他人对拍，判断正误。互测中我一直使用这种黑箱方法测试，没有根据程序代码的特定结构修改过测评机。

​● 利用实用工具寻找bug。由于三次作业我均使用正则表达式进行匹配，所以使用了RegexBuddy软件检验自己正则表达式的正确性。我也是利用该软件发现书写表达式类的正则表达式时，由于正则过长，会导致许多无法避免的歧义，而换为头尾匹配+验证项前符号的方法。

四 重构经历总结

这三次作业，我的架构是基本统一的，每一次都在上一次的基础上扩展，其中在第二次作业时进行了一次大扩展。主要原因是第一次作业想得过于简单，混淆了项和因子的概念。在第二次作业中，我仔细确定了因子和项的关系，即多个因子相乘得到项，并新建了相应的5个因子类，实现了一个方便继承的抽象类，在原架构的基础上实现了极大扩展。

这给我的启示是，在写程序的时候不能过拟合题目要求，我们需要透过现象看本质。对于第一次作业来讲，新建因子类可能确实会使程序更加复杂， 但它才是多项式求导的本质逻辑。今后我也需要多思考，在架构上多花些心思。

五 心得体会

OO的第一单元作业对我还是非常具有挑战性的，尤其是第二次作业，差点就觉得自己的面向对象之旅止步于此了。在这个煎熬的过程中，我也收获了许多启示：

​● 花在设计上滴水之恩总会在写代码的时刻涌泉相报回自己。永远不要着急上手写代码，前期设计非常重要。我就是因为自以为是，到了第三次没有仔细设计，导致hw3连中测都通过得极为艰辛。根本没意识倒自己的输出中会存在sin()这类式子。

​● 到底什么是面向对象？这个问题一直困扰着我。直到有一天，我和一位朋友抱怨我不会面向对象。他告诉我：“面向对象和面向过程的区别，其实可以非常直观地理解。面向过程编程时，你想的是程序运行和解题的过程，并由此构建一个个函数；但面向对象编程时，你不会去思考过程，你想的是能用到哪些类，类之间的关系是怎样的......”。由他的话再回想我这三周的训练，我突然茅塞顿开。面向对象是一种思想，需要我们在编程的过程里不断体验，一句两句话真的说不清楚，它是一种构思方式，潜移默化间早已拓展了我们编程的方法。突然就觉得，花在OO上的光阴没有白白流逝。

​● 拒绝拖延。这个或许不用过多解释了，每个周五都悠闲自在，每个周日都急得想哭...以后不能再这样了。

​● 不要因为自己的怠惰造成无法弥补的后果。hw3的中测我过得极为艰难，感觉把自己累着了（其实就是周六下午才开始正儿八经构思代码，开始得太晚，做得太急，给吓着了）...虽然周日还有一个下午和晚上，我并没有再形式建模通读代码，一直在佛系改琐碎的bug。也一直在电脑前坐着，但就很虚度光阴，很怠惰。于是终于在强测中付出了代价。所以，做人还是不能太懒（哭）。