P1601 A+B Problem（高精）

P1601 A+B Problem（高精）

高精度加法，相当于a+b problem，不用考虑负数.

输入格式

分两行输入。a,b \leq 10^{500}a,b≤10500

输出格式

输出只有一行，代表a+ba+b的值

输入输出样例

输入 #1复制

1
1

输出 #1复制

2

输入 #2复制

1001
9099

输出 #2复制

10100

#include<bits/stdc++.h>
using namespace std;
int main()
{
	string s1,s2;
	int a[250],b[250],h;
	memset(a,0,sizeof(a));
	memset(b,0,sizeof(b));
	cin>>s1>>s2;
	a[0]=s1.length();
	b[0]=s2.length();
	for(int i=1;i<=a[0];i++)
		a[i]=s1[a[0]-i]-'0';//把第一个字符串转换为整数，存放在数组a中
	for(int i=1;i<=b[0];i++)
		b[i]=s2[b[0]-i]-'0';//把第二个字符串转换为整数，存放在数组b中
	h=(a[0]>b[0]?a[0]:b[0]);    //取两个字符串最大的长度
	for(int i=1;i<=h;i++)       //做按位加法，同时处理进位
	{
		a[i]+=b[i];
		a[i+1]+=a[i]/10;
		a[i]%=10;
	}
	h++;
	if(a[h]==0&&h>1)
		h--;
	for(int i=h;i>0;i--)
		cout<<a[i];
	return 0;
}

s1[a[0]-i]-'0'

因为ASCII字符中的数字（‘123456’）想转换为纯数字（1,2,3,4...）就要减去48（ASCII单位），而‘0’的ASCII单位正好等于48。

 

一、高精度加法：

高精度加法的实现原理：

1、计算结果的位数
358934760892734899共18位
38960302975237462共17位
故结果不会超过19位。
2、将要计算的数字分割成多段，按照顺序排列（这里以0-32767作为每一存储单位存储的数的限制）：

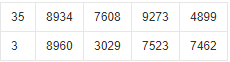
（为提高空间利用效率，可以一个存储单位存储多位数。）
3、将两数相加。

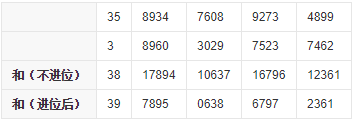
4、输出结果。
从高位到低位依次输出。除最高位以外，其他低位上不足4位的要在前面补上0。