解码AVL树

为什么要关注二叉树的平衡性？—— 从 BST 的缺陷说起

二叉搜索树（BST）的核心优势是 “高效搜索”：利用 “左子树所有节点值＜根节点值＜右子树所有节点值” 的特性，能从根节点开始快速定位目标节点。但 BST 有个致命缺陷 ——无法保证树的结构平衡，极端情况下会 “退化”，彻底丧失高效性。

BST 的退化现象

BST 的结构完全依赖节点插入顺序，若插入的节点值是 “有序的”（比如从小到大或从大到小），树会退化成一条 “链表”。

例子：有序插入导致 BST 退化

假设创建空 BST 后，依次插入节点值 1、2、3、4、5，最终树的结构如下：

这种结构虽然仍满足 BST 的定义（左小右大），但本质是单链表—— 每个节点只有右子树，没有左子树。

退化对性能的影响

BST 的性能取决于 “树的高度”：

平衡的 BST：高度约为 log₂n（n 是节点总数），搜索时最多需要比较 log₂n 次，时间复杂度为 O(log₂n)。比如 n=1000 时，log₂1000≈10，只需比较 10 次。
退化的 BST（链表）：高度等于 n，搜索时需要从根遍历到最后一个节点，时间复杂度退化为 O(n)。比如 n=1000 时，最多需要比较 1000 次，效率大幅下降。

因此，我们需要一种 “自平衡的 BST”—— 既能保持 BST 的搜索特性，又能在插入 / 删除节点后自动调整结构，避免退化，这就是 “平衡树” 的核心需求。

平衡树的定义（量化 “平衡”）

要实现 “自平衡”，首先得明确：什么是 “平衡”？平衡树的严格定义：树中任意一个节点的左、右子树的高度差（称为 “平衡因子”）的绝对值 ≤ 1。

高度与平衡因子

节点的高度：从该节点到 “最远叶子节点” 的路径上的节点总数（空树高度约定为 0，单个节点高度为 1）。
- 例：空树高度 = 0；只有根节点时，根的高度 = 1；根有左子节点时，根的高度 = max (左子树高度，右子树高度)+1=max (1,0)+1=2。
平衡因子：某节点的 “左子树高度 - 右子树高度”。平衡树要求所有节点的平衡因子 ∈ {-1, 0, 1}（绝对值≤1）。

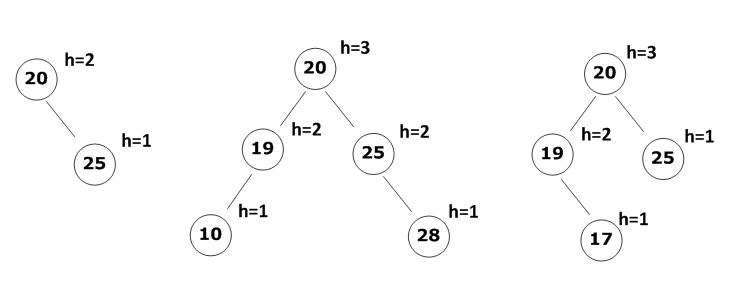
例子：平衡树与非平衡树的对比

平衡树（所有节点平衡因子≤1）

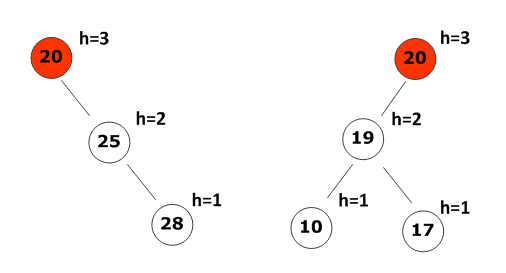
非平衡树（存在节点平衡因子＞1）

AVL 树 —— 严格自平衡的二叉搜索树

AVL 树是最早实现 “自平衡” 的 BST，由 Adelson-Velsky 和 Landis 提出，因此得名。AVL 树的核心定义：既是二叉搜索树（满足左小右大），又是平衡树（所有节点平衡因子∈{-1,0,1}）。

AVL 树的关键能力是：插入或删除节点后，若树出现不平衡，能通过 “旋转” 操作快速恢复平衡，且旋转后仍保持 BST 的特性。

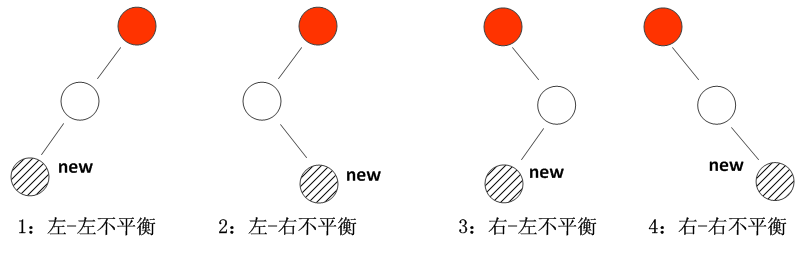
AVL 树不平衡的四种类型（插入 / 删除均可能导致）

插入或删除节点后，不平衡只会出现在 “从操作节点到根节点的路径上”，且不平衡的根源可归为四种类型，核心区别是 “不平衡节点的哪一侧子树过高，以及过高子树的哪一侧又过高”。

先明确两个概念：

失衡节点：平衡因子绝对值＞1 的节点（是不平衡的根源）；
高子树：失衡节点中高度更高的那一侧子树（左高或右高）。

四种不平衡类型如下：

类型	定义（以失衡节点为核心）
左左不平衡	失衡节点左子树过高（平衡因子＞1），且左子树的左子树更高（左子树平衡因子≥0）
左右不平衡	失衡节点左子树过高（平衡因子＞1），且左子树的右子树更高（左子树平衡因子＜0）
右左不平衡	失衡节点右子树过高（平衡因子＜-1），且右子树的左子树更高（右子树平衡因子＞0）
右右不平衡	失衡节点右子树过高（平衡因子＜-1），且右子树的右子树更高（右子树平衡因子≤0）

注：插入操作最多只会导致 1 个节点失衡；删除操作可能导致多个节点失衡，需从失衡节点向上回溯检查，直到根节点。

解决不平衡的核心操作 —— 旋转

旋转是 AVL 树恢复平衡的关键，本质是 “调整节点的父子关系”，分为基础旋转（左旋、右旋） 和复合旋转（左右旋、右左旋），每种不平衡类型对应一种旋转方案。

旋转的核心要求：

旋转后必须恢复平衡（所有节点平衡因子≤1）；
旋转后必须保持 BST 特性（左小右大）。

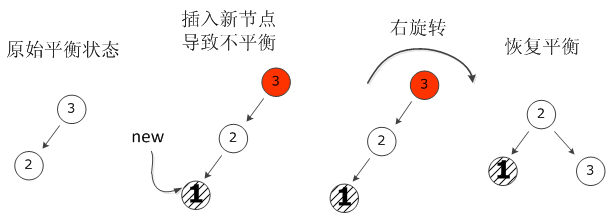
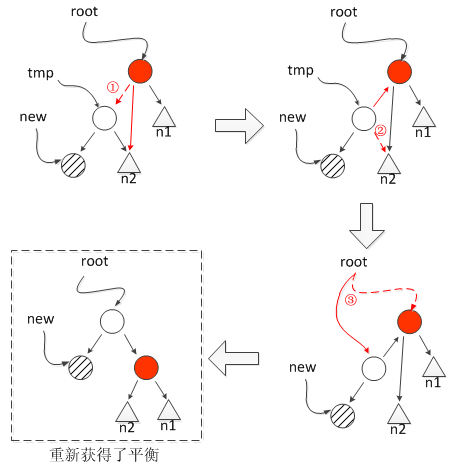
基础旋转 1：右旋（处理 “左左不平衡”）

当失衡节点是 “左左不平衡” 时，用右旋将 “左子树提为新根”，降低左子树高度，恢复平衡。

基础旋转 2：左旋（处理 “右右不平衡”）

左旋是右旋的 “镜像操作”，用于处理 “右右不平衡”，核心是将 “右子树提为新根”，降低右子树高度。

复合旋转 1：左右旋（处理 “左右不平衡”）

“左右不平衡” 是 “左子树的右子树过高”，无法用单次右旋解决，需分两步：先对左子树做左旋，将其转为 “左左不平衡”，再对失衡节点做右旋。

复合旋转 2：右左旋（处理 “右左不平衡”）

右左旋是左右旋的 “镜像操作”，用于处理 “右子树的左子树过高”，步骤：先对右子树做右旋，转为 “右右不平衡”，再对失衡节点做左旋。

四种不平衡类型与旋转方案对应表

不平衡类型	解决步骤	核心逻辑
左左不平衡	对失衡节点直接右旋	左子树过高，提左子树为新根
左右不平衡	1. 对失衡节点的左子树左旋；2. 对失衡节点右旋	先将 “左右” 转为 “左左”，再右旋
右右不平衡	对失衡节点直接左旋	右子树过高，提右子树为新根
右左不平衡	1. 对失衡节点的右子树右旋；2. 对失衡节点左旋	先将 “右左” 转为 “右右”，再左旋

AVL 树的代码设计

了解了 AVL 树的平衡原理和旋转操作后，我们可以通过代码实现这一数据结构。核心包括节点设计、旋转函数、插入和删除操作，每个部分都需围绕 “维持平衡” 展开。

树节点设计

AVL 树的节点比普通二叉搜索树（BST）多一个关键信息 ——子树高度，这是判断平衡的基础。

节点结构体定义

typedef int datatype; // 节点存储的数据类型（可根据需求修改）

typedef struct node {
    datatype data;       // 节点数据
    int height;          // 以当前节点为根的子树高度（用于计算平衡因子）
    struct node *lchild; // 左子树指针
    struct node *rchild; // 右子树指针
} treenode, *linktree; // treenode为节点类型，linktree为节点指针类型

为什么需要 “height” 字段？

平衡因子 = 左子树高度 - 右子树高度，AVL 树要求所有节点的平衡因子绝对值 ≤ 1；
每次插入、删除或旋转后，必须更新节点高度，否则平衡判断会出错；
约定：空树的高度为 - 1（叶子节点的左右子树为空，因此叶子节点高度 = max (-1, -1) + 1 = 0，计算更合理）。

旋转操作的代码实现

旋转是 AVL 树恢复平衡的核心，需通过代码实现右旋转、左旋转、左右旋转和右左旋转，确保旋转后既平衡又保持 BST 特性。

辅助函数

计算节点高度：处理空节点的情况（返回 - 1）；
取最大值：用于计算子树高度。

// 宏定义：取两个整数的最大值
#define MAX(a, b) ((a) > (b) ? (a) : (b))
// 辅助函数：获取节点高度（空节点返回-1）
int height(linktree node) {
    return (node == NULL) ? -1 : node->height;
}

右旋转（处理左左不平衡）

场景：节点左子树高度比右子树高 2，且左子树的左子树更高。

linktree avlRotateRight(linktree root) {
    // 步骤1：记录root的左子树（tmp将成为新根）
    linktree tmp = root->lchild;

    // 步骤2：调整指针关系
    root->lchild = tmp->rchild; // root的左子树改为tmp的右子树
    tmp->rchild = root;         // tmp的右子树改为root

    // 步骤3：更新高度（先更新root，再更新tmp）
    root->height = MAX(height(root->lchild), height(root->rchild)) + 1;
    tmp->height = MAX(height(tmp->lchild), root->height) + 1;

    return tmp; // 返回新根tmp
}

示例：左左不平衡经右旋转后平衡

旋转前（左左不平衡）       旋转后（平衡）
    3 (root)                2 (新根)
   /                       / \
  2 (tmp)         →       1   3
 /
1

左旋转（处理右右不平衡）

场景：节点右子树高度比左子树高 2，且右子树的右子树更高。

linktree avlRotateLeft(linktree root) {
    // 步骤1：记录root的右子树（tmp将成为新根）
    linktree tmp = root->rchild;

    // 步骤2：调整指针关系
    root->rchild = tmp->lchild; // root的右子树改为tmp的左子树
    tmp->lchild = root;         // tmp的左子树改为root

    // 步骤3：更新高度（先更新root，再更新tmp）
    root->height = MAX(height(root->lchild), height(root->rchild)) + 1;
    tmp->height = MAX(root->height, height(tmp->rchild)) + 1;

    return tmp; // 返回新根tmp
}

示例：右右不平衡经左旋转后平衡

旋转前（右右不平衡）       旋转后（平衡）
1 (root)                    2 (新根)
 \                         / \
  2 (tmp)         →       1   3
   \
    3

左右旋转（处理左右不平衡）

场景：节点左子树高度比右子树高 2，且左子树的右子树更高。本质：先对左子树左旋转，再对原节点右旋转。

linktree avlRotateLeftRight(linktree root) {
    root->lchild = avlRotateLeft(root->lchild); // 先左旋转左子树
    return avlRotateRight(root);                // 再右旋转root
}

示例：左右不平衡经左右旋转后平衡

旋转前（左右不平衡）      第一步：左旋转左子树      第二步：右旋转root（平衡）
    3 (root)                3 (root)               2 (新根)
   /                       /                      / \
  1                        2              →       1   3
   \                      /
    2                    1

右左旋转（处理右左不平衡）

场景：节点右子树高度比左子树高 2，且右子树的左子树更高。本质：先对右子树右旋转，再对原节点左旋转。

linktree avlRotateRightLeft(linktree root) {
    root->rchild = avlRotateRight(root->rchild); // 先右旋转右子树
    return avlRotateLeft(root);                  // 再左旋转root
}

示例：右左不平衡经右左旋转后平衡

旋转前（右左不平衡）      第一步：右旋转右子树      第二步：左旋转root（平衡）
1 (root)                    1 (root)               2 (新根)
 \                         \                      / \
  3                         2              →       1   3
 /                           \
2                             3

插入节点操作

AVL 树的插入需先遵循 BST 的插入规则，再检查平衡，若失衡则旋转调整，最后更新高度。

插入步骤

BST 插入：根据节点值大小插入到左 / 右子树（空树直接作为根，重复值不插入）；
平衡检查：计算当前节点的平衡因子，若绝对值为 2，判断失衡类型并旋转；
更新高度：根据左右子树高度更新当前节点高度。

代码实现

// 辅助函数：创建新节点
linktree createNode(datatype data) {
    linktree newNode = (linktree)malloc(sizeof(treenode));
    newNode->data = data;
    newNode->height = 0; // 新节点为叶子，高度0（左右子树为空，高度-1）
    newNode->lchild = newNode->rchild = NULL;
    return newNode;
}

// AVL树插入函数
linktree avlInsert(linktree root, datatype data) {
    // 步骤1：按BST规则插入新节点
    if (root == NULL) {
        return createNode(data); // 空树，新节点为根
    }

    if (data < root->data) {
        root->lchild = avlInsert(root->lchild, data); // 插入左子树
    } 
    else if (data > root->data) {
        root->rchild = avlInsert(root->rchild, data); // 插入右子树
    } 
    else {
        printf("数据 %d 已存在，不插入\n", data); // 重复值处理
        return root;
    }

    // 步骤2：检查平衡并旋转
    int balance = height(root->lchild) - height(root->rchild); // 平衡因子

    // 左子树过高（平衡因子=2）
    if (balance == 2) {
        // 左左不平衡：新节点在左子树的左边
        if (data < root->lchild->data) {
            root = avlRotateRight(root);
        }
        // 左右不平衡：新节点在左子树的右边
        else if (data > root->lchild->data) {
            root = avlRotateLeftRight(root);
        }
    }
    // 右子树过高（平衡因子=-2）
    else if (balance == -2) {
        // 右右不平衡：新节点在右子树的右边
        if (data > root->rchild->data) {
            root = avlRotateLeft(root);
        }
        // 右左不平衡：新节点在右子树的左边
        else if (data < root->rchild->data) {
            root = avlRotateRightLeft(root);
        }
    }

    // 步骤3：更新当前节点高度
    root->height = MAX(height(root->lchild), height(root->rchild)) + 1;

    return root;
}

删除节点操作

删除比插入更复杂：先按 BST 规则删除节点，再从删除位置向上回溯检查平衡，可能需要多次旋转，最后更新高度。

删除步骤

BST 删除：

叶子节点：直接释放；
单子女节点：用子女替换；
双子女节点：用左子树最大值（前驱）或右子树最小值（后继）替换，再删除前驱 / 后继；

平衡检查：计算平衡因子，若绝对值为 2，通过子树高度差判断失衡类型并旋转；

更新高度：更新当前节点高度。

代码实现

linktree avlRemove(linktree root, datatype data) {
    // 步骤1：按BST规则删除节点
    if (root == NULL) {
        return NULL; // 树空或未找到节点
    }

    if (data < root->data) {
        root->lchild = avlRemove(root->lchild, data); // 左子树删除
    } 
    else if (data > root->data) {
        root->rchild = avlRemove(root->rchild, data); // 右子树删除
    } 
    else {
        // 找到删除节点
        linktree temp;

        // 情况1：单子女或无子女
        if (root->lchild == NULL) {
            temp = root->rchild;
            free(root);
            return temp;
        } 
        else if (root->rchild == NULL) {
            temp = root->lchild;
            free(root);
            return temp;
        }

        // 情况2：双子女→用左子树最大值（前驱）替换
        temp = root->lchild;
        while (temp->rchild != NULL) {
            temp = temp->rchild; // 找左子树最右节点（最大值）
        }
        root->data = temp->data; // 替换值
        root->lchild = avlRemove(root->lchild, temp->data); // 删除前驱
    }

    // 若删除后树空，直接返回
    if (root == NULL) {
        return NULL;
    }

    // 步骤2：检查平衡并旋转
    int balance = height(root->lchild) - height(root->rchild);

    // 左子树过高（平衡因子=2）
    if (balance == 2) {
        // 左子树的左子树更高→左左不平衡（右旋转）
        if (height(root->lchild->lchild) >= height(root->lchild->rchild)) {
            root = avlRotateRight(root);
        }
        // 左子树的右子树更高→左右不平衡（左右旋转）
        else {
            root = avlRotateLeftRight(root);
        }
    }
    // 右子树过高（平衡因子=-2）
    else if (balance == -2) {
        // 右子树的右子树更高→右右不平衡（左旋转）
        if (height(root->rchild->rchild) >= height(root->rchild->lchild)) {
            root = avlRotateLeft(root);
        }
        // 右子树的左子树更高→右左不平衡（右左旋转）
        else {
            root = avlRotateRightLeft(root);
        }
    }

    // 步骤3：更新当前节点高度
    root->height = MAX(height(root->lchild), height(root->rchild)) + 1;

    return root;
}

代码设计的核心注意事项

高度实时更新：任何操作（插入、删除、旋转）后必须更新节点高度，否则平衡因子计算错误；
旋转的指针调整：旋转时需准确修改父子节点指针，避免断链或破坏 BST 特性；
删除的回溯检查：删除可能导致多个节点失衡，需从删除位置向上检查至根节点；
空节点处理：计算高度和访问子树时，需先判断节点是否为空，避免空指针错误。

AVL 树的核心特性与应用场景

核心特性

严格平衡：所有节点平衡因子∈{-1,0,1}，树的高度严格控制在 O (log₂n)；
保持 BST 特性：旋转操作不会破坏 “左小右大”，因此搜索、插入、删除的逻辑都基于 BST；
时间复杂度：搜索、插入、删除均为 O (log₂n)，比普通 BST 更稳定；
自调整：插入 / 删除后通过旋转自动恢复平衡，无需人工干预。

应用场景

AVL 树适合对 “查询效率要求极高” 且 “插入 / 删除频率不高” 的场景，比如：

数据库索引（早期部分数据库用 AVL 树，后来更多用红黑树，因红黑树旋转次数更少）；
有序数据的快速查询（如字典、通讯录的按名查询）。

注：AVL 树的缺点是 “旋转次数多”—— 插入 / 删除可能需要多次旋转（尤其是删除），因此在插入 / 删除频繁的场景中，性能不如红黑树（红黑树是 “近似平衡”，旋转次数更少）。

posted @ 2025-10-02 14:48 YouEmbedded 阅读(3) 评论(0) 收藏举报

刷新页面返回顶部

YouEmbedded