多项式例题3
CF954I Yet Another String Matching Problem
Suppose you have two strings $ s $ and $ t $ , and their length is equal. You may perform the following operation any number of times: choose two different characters $ c_{1} $ and $ c_{2} $ , and replace every occurence of $ c_{1} $ in both strings with $ c_{2} $ . Let's denote the distance between strings $ s $ and $ t $ as the minimum number of operations required to make these strings equal. For example, if $ s $ is abcd and $ t $ is ddcb, the distance between them is $ 2 $ — we may replace every occurence of a with b, so $ s $ becomes bbcd, and then we may replace every occurence of b with d, so both strings become ddcd.
You are given two strings $ S $ and $ T $ . For every substring of $ S $ consisting of $ |T| $ characters you have to determine the distance between this substring and $ T $ .
Input
The first line contains the string $ S $ , and the second — the string $ T $ ( $ 1<=|T|<=|S|<=125000 $ ). Both strings consist of lowercase Latin letters from a to f.
Output
Print $ |S|-|T|+1 $ integers. The $ i $ -th of these integers must be equal to the distance between the substring of $ S $ beginning at $ i $ -th index with length $ |T| $ and the string $ T $ .
考虑两个串对每个字符进行匹配,如果对 \(S\) 串的字符 \(C_1\) 与 \(T\) 串的字符 \(C_2\) 能够发生匹配,那么我们需要用一次操作把 \(C_1\) 和 \(C_2\) 当成同一个字符,因此预处理后考虑并查集即可。
朴素的实现需要 \(6 \times 2 = 12\) 次 FFT,\(6 \times 6 = 36\) 次 IDFT,容易发现我们只有不同的对才有意义,因此可以简化为 \(5 + 4 + 3 + 2 + 1 = 15\) 次 IDFT,总共进行 \(27\) 次 NTT 操作,我们的时间复杂度为 \(O(k|\Sigma|n\log{n})\),其中 \(k\) 取 \(27\),\(|\Sigma|\) 取 \(6\),可以接受。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define ull unsigned long long
#define PII pair<ll, ll>
#define pb push_back
#define clr(f, n) memset(f, 0, sizeof(int) * (n))
#define cpy(f, g, n) memcpy(f, g, sizeof(int) * (n))
#define rev(f, n) reverse(f, f + (n))
const int N = 2e5 + 10, _G = 3, mod = 998244353;
ll qpow(ll a, ll k = mod - 2) {
ll res = 1;
while (k) {
if (k & 1) res = res * a % mod;
k >>= 1;
a = a * a % mod;
}
return res;
}
const int invG = qpow(_G);
int rev[N << 1], rev_len;
void rev_init(int n) {
if (rev_len == n) return;
for (int i = 0; i < n; i ++ ) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? n >> 1 : 0);
rev_len = n;
}
void NTT(int *g, int op, int n) {
rev_init(n);
static ull f[N << 1], Gk[N << 1] = {1};
for (int i = 0; i < n; i ++ ) f[i] = g[rev[i]];
for (int k = 1; k < n; k <<= 1) {
int G1 = qpow(~op ? _G : invG, (mod - 1) / (k << 1));
for (int i = 1; i < k; i ++ ) Gk[i] = Gk[i - 1] * G1 % mod;
for (int i = 0; i < n; i += k << 1) {
for (int j = 0; j < k; j ++ ) {
int tmp = Gk[j] * f[i | j | k] % mod;
f[i | j | k] = f[i | j] + mod - tmp;
f[i | j] += tmp;
}
}
if (k == (1 << 10)) for (int i = 0; i < n; i ++ ) f[i] %= mod;
}
if (~op) for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod;
else {
int invn = qpow(n);
for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod * invn % mod;
}
}
int n, m;
string s, t;
int F[6][N << 1], G[6][N << 1];
int H[6][6][N << 1];
int p[6];
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void solve() {
cin >> s >> t;
n = s.length(), m = t.length();
for (int i = 0; i < n; i ++ ) F[s[i] - 'a'][i] = 1;
for (int i = 0; i < m; i ++ ) G[t[i] - 'a'][m - i - 1] = 1;
int len; for (len = 1; len < n + m - 1; len <<= 1);
for (int i = 0; i < 6; i ++ ) NTT(F[i], 1, len), NTT(G[i], 1, len);
for (int i = 0; i < 6; i ++ ) {
for (int j = i + 1; j < 6; j ++ ) {
for (int k = 0; k < len; k ++ ) {
H[i][j][k] = (1ll * F[i][k] * G[j][k] + 1ll * F[j][k] * G[i][k]) % mod;
}
NTT(H[i][j], -1, len);
}
}
for (int k = m - 1; k < n; k ++ ) {
int res = 0;
for (int i = 0; i < 6; i ++ ) p[i] = i;
for (int i = 0; i < 6; i ++ ) {
for (int j = i + 1; j < 6; j ++ ) {
if (find(i) == find(j) || !H[i][j][k]) continue;
p[find(j)] = find(i), res ++ ;
}
}
cout << res << " ";
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
// cin >> T;
while (T -- ) solve();
return 0;
}
CF1334G Substring Search
You are given a permutation $ p $ consisting of exactly $ 26 $ integers from $ 1 $ to $ 26 $ (since it is a permutation, each integer from $ 1 $ to $ 26 $ occurs in $ p $ exactly once) and two strings $ s $ and $ t $ consisting of lowercase Latin letters.
A substring $ t' $ of string $ t $ is an occurence of string $ s $ if the following conditions are met:
- $ |t'| = |s| $ ;
- for each \(i \in [1, |s|]\) , either \(s_i = t'_i\) , or \(p_{idx(s_i)} = idx(t'_i)\) , where $ idx(c) $ is the index of character $ c $ in Latin alphabet ( $ idx(\text{a}) = 1 $ , $ idx(\text{b}) = 2 $ , $ idx(\text{z}) = 26 $ ).
For example, if $ p_1 = 2 $ , $ p_2 = 3 $ , $ p_3 = 1 $ , $ s = \text{abc} $ , $ t = \text{abcaaba} $ , then three substrings of $ t $ are occurences of $ s $ (they are $ t' = \text{abc} $ , $ t' = \text{bca} $ and $ t' = \text{aba} $ ).
For each substring of $ t $ having length equal to $ |s| $ , check if it is an occurence of $ s $ .
Input
The first line contains $ 26 $ integers $ p_1 $ , $ p_2 $ , ..., $ p_{26} $ ( $ 1 \le p_i \le 26 $ , all these integers are pairwise distinct).
The second line contains one string $ s $ , and the third line contains one string $ t $ ( $ 2 \le |s| \le |t| \le 2 \cdot 10^5 $ ) both consisting of lowercase Latin letters.
Output
Print a string of $ |t| - |s| + 1 $ characters, each character should be either 0 or 1. The $ i $ -th character should be 1 if and only if the substring of $ t $ starting with the $ i $ -th character and ending with the $ (i + |s| - 1) $ -th character (inclusive) is an occurence of $ s $ .
为了使两个字符串匹配,我们定义匹配函数 \(C(x, \, y) = (x - y)^2(x - p_y)^2\),当且仅当 \(C(x, \, y) = 0\) 时两个字符匹配,这个式子展开过于庞大,太不优秀,我们简化为 \(C(x, \, y) = (x - y)(x - p_y) = x^2 - (p_y + y)x + yp_y\),通过对每个字符随机赋值计算,错误率为 \(\frac{d}{mod}\),构建字符串匹配函数并大力展开,得到
翻转得到
不难发现 \(\sum\limits_{i = 1}^mS^2(i + j)\) 和 \(\sum\limits_{i = 1}^mT(i)P_T(i)\) 均为常数,拿出来即可。
卷积后检测位置是否为 \(0\) 即可。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define ull unsigned long long
#define PII pair<ll, ll>
#define pb push_back
#define clr(f, n) memset(f, 0, sizeof(int) * (n))
#define cpy(f, g, n) memcpy(f, g, sizeof(int) * (n))
#define rev(f, n) reverse(f, f + (n))
const int N = 4e5 + 10, _G = 3, mod = 998244353;
ll qpow(ll a, ll k = mod - 2) {
ll res = 1;
while (k) {
if (k & 1) res = res * a % mod;
k >>= 1;
a = a * a % mod;
}
return res;
}
const int invG = qpow(_G);
int rev[N << 1], rev_len;
void rev_init(int n) {
if (rev_len == n) return;
for (int i = 0; i < n; i ++ ) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? n >> 1 : 0);
rev_len = n;
}
void NTT(int *g, int op, int n) {
rev_init(n);
static ull f[N << 1], Gk[N << 1] = {1};
for (int i = 0; i < n; i ++ ) f[i] = g[rev[i]];
for (int k = 1; k < n; k <<= 1) {
int G1 = qpow(~op ? _G : invG, (mod - 1) / (k << 1));
for (int i = 1; i < k; i ++ ) Gk[i] = Gk[i - 1] * G1 % mod;
for (int i = 0; i < n; i += k << 1) {
for (int j = 0; j < k; j ++ ) {
int tmp = Gk[j] * f[i | j | k] % mod;
f[i | j | k] = f[i | j] + mod - tmp;
f[i | j] += tmp;
}
}
if (k == (1 << 10)) for (int i = 0; i < n; i ++ ) f[i] %= mod;
}
if (~op) for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod;
else {
int invn = qpow(n);
for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod * invn % mod;
}
}
void px(int *f, int *g, int n) {
for (int i = 0; i < n; i ++ ) f[i] = 1ll * f[i] * g[i] % mod;
}
void covolution(int *f, int *g, int len, int lim) {
static int sav[N << 1];
int n; for (n = 1; n < len << 1; n <<= 1);
clr(sav, n); cpy(sav, g, n);
NTT(sav, 1, n); NTT(f, 1, n);
px(f, sav, n); NTT(f, -1, n);
clr(f + lim, n - lim), clr(sav, n);
}
int n, m, p[27], value[27];
string s, t;
int F[N << 1], G[N << 1];
int H[N << 1];
void solve() {
for (int i = 0; i < 26; i ++ ) cin >> p[i], p[i] -- , value[i] = ((rand() << 15) + rand()) % mod;
cin >> t >> s;
n = s.length(), m = t.length();
for (int i = 0; i < n; i ++ ) F[i + 1] = 1ll * value[s[i] - 'a'] * value[s[i] - 'a'] % mod;
for (int i = 1; i <= n; i ++ ) F[i] = (F[i] + F[i - 1]) % mod;
for (int i = 0; i <= n - m; i ++ ) H[i] += (F[i + m] - F[i] + mod) % mod;
clr(F, n + 1);
for (int i = 0; i < n; i ++ ) F[i] = value[s[i] - 'a'];
for (int i = 0; i < m; i ++ ) G[i] = value[t[m - i - 1] - 'a'] + value[p[t[m - i - 1] - 'a']];
covolution(F, G, n + m >> 1, n + m - 1);
for (int i = 0; i <= n - m; i ++ ) H[i] -= F[i + m - 1];
clr(F, n + m - 1); clr(G, m);
ll res = 0;
for (int i = 0; i < m; i ++ ) res += 1ll * value[t[i] - 'a'] * value[p[t[i] - 'a']] % mod;
for (int i = 0; i <= n - m; i ++ ) {
if ((H[i] + res) % mod == 0) cout << 1;
else cout << 0;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
// cin >> T;
while (T -- ) solve();
return 0;
}
CF1251F Red-White Fence
Polycarp想在他家附近建一道栅栏。他有\(n\)个白板和\(k\)个红板去建造它。每一块板都有一个整数长度。
一个好的栅栏应由一块红板和几块(可能是零块)白板组成。红色的板应该在这道栅栏中是最长的,而且红板前的板子长度应为递增,而红板之后的板子长度为递减。如果用了\(m\)块板子,它们的长度从左到右依次是\(l_1,l_2,…,l_m\),那么应该符合以下条件
①栅栏上应有且只有一块红板,设其序号为\(j\)
②对于所有的\(i∈[1,j-1]\)有\(l_i<l_{i+1}\)
③对于所有的\(i∈[j,m-1]\)有\(l_i>l_{i+1}\)
在Polycarp建造他的栅栏时,他会从左向右在\(0\)高度上放置所有板,没有间隙,所以这些板将会组成一个多边形:
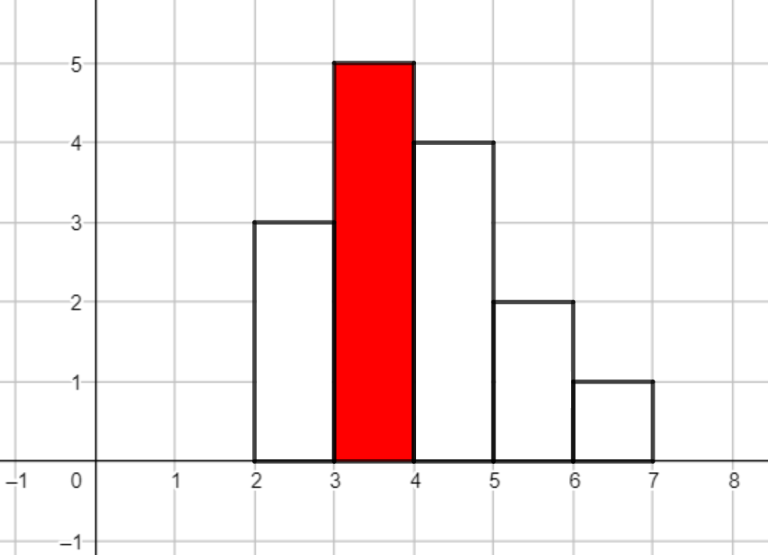
例图:一个栅栏的板长数组为\([3,5,4,2,1]\),第二个板是红板。栅栏的周长是\(20\)。Polycrp对一些特殊周长的栅栏感兴趣。他有喜欢的\(q\)个偶整数\([Q_1,Q_2,…,Q_q]\),对于每个这样的整数\(Q_i\),他想计算有几种不同的周长是\(Q_i\)的篱笆可以被造出来(如果两个篱笆的板长排列不同,那么就认为这两个篱笆是不同的)你可以帮他计算这些数值吗?
输入格式
输入第一行是两个正整数\(n,k(1≤n≤3*10^5,1≤k≤5)\),表示Polycarp拥有的白板和红板的数量
第二行有\(n\)个正整数\([a_1,a_2,...,a_n](1≤a_i≤3*10^5)\),表示Polycarp拥有的\(n\)块白板的长度
第三行有\(k\)个正整数\([b_1,b_2,...,b_k](1≤b_i≤3*10^5)\),表示Polycarp拥有的\(k\)块红板的长度,所有\(b_i\)都是不相同的
第四行是一个正整数\(q(1≤q≤3*10^5)\),表示特殊周长的数量
第五行有\(q\)个正整数\([Q_1,Q_2,...,Q_q](4≤Q_i≤12*10^5)\),每个\(Q_i\)都是偶数,表示Polycarp喜欢的特殊整数(即特殊周长)
输出格式
对于每个\(Q_i\),输出一个整数,表示有多少种符合约束条件的周长为\(Q_i\)的栅栏,由于数量可能很大,结果请对\(998244353\)取模,每个输出占一行
首先对条件进行分析,为什么白板和红板要分开输入?有给我们枚举红板进行预处理的可能性,先不管周长,因为我们发现周长唯一由选的板数和红板的长度决定,与白板是多少无关。
通过枚举一个红板,我们考虑哪些白板可以产生贡献,显然只有小于红板长度的白板有意义,我们可以怎么放置呢?不难看出,如果不放白板,贡献为乘 \(1\),放一个,可以放在左或右,贡献为乘 \(2\),如果放两个,是唯一的,因为不允许连续两个板子的长度相等,贡献依旧为 \(1\),更多的板子没有意义,如果设 \(F_i(x)\) 为板长为 \(i\) 的白板的贡献函数,显然可得
容易得到红板的生成函数
那么其系数 \([x^i]G_j(x)\) 表示选择 \(i\) 块白板,且红板为 \(b_j\) 的方案数,通过分治算法卷积,我们可以得到一个 \(O(n\log^2{n})\) 的算法。
更具体一点,我们发现只有两种有意义的生成函数,一个板子的贡献为 \(F(x) = 1 + 2x\),两个板子的贡献为 \(F'(x) = 1 + 2x + x^2 = (x + 1)^2\),这告诉我们,实际有意义的数据只有比红板矮的板子中,有一个板子还是有多余一个板子的不同板子个数。
我们只用对 \(F(x) = 2x + 1\) 和 \(F'(x) = x^2 + 2x + 1\) 求一个快速幂即可,我们通过倍增算法实现,复杂度是 \(O(n\log{n})\) 的,多项式 \(\exp\) 套 \(\ln\) 也是可以的,不过复杂度是 \(O(nk\log{nk})\),难以通过。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define ull unsigned long long
#define PII pair<ll, ll>
#define pb push_back
#define clr(f, n) memset(f, 0, sizeof(int) * (n))
#define cpy(f, g, n) memcpy(f, g, sizeof(int) * (n))
#define rev(f, n) reverse(f, f + (n))
const int N = 1.1e6 + 10, _G = 3, mod = 998244353;
ll qpow(ll a, ll k = mod - 2) {
ll res = 1;
while (k) {
if (k & 1) res = res * a % mod;
k >>= 1;
a = a * a % mod;
}
return res;
}
const int invG = qpow(_G);
int rev[N << 1], rev_len;
void rev_init(int n) {
if (rev_len == n) return;
for (int i = 0; i < n; i ++ ) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? n >> 1 : 0);
rev_len = n;
}
void NTT(int *g, int op, int n) {
rev_init(n);
static ull f[N << 1], Gk[N << 1] = {1};
for (int i = 0; i < n; i ++ ) f[i] = g[rev[i]];
for (int k = 1; k < n; k <<= 1) {
int G1 = qpow(~op ? _G : invG, (mod - 1) / (k << 1));
for (int i = 1; i < k; i ++ ) Gk[i] = Gk[i - 1] * G1 % mod;
for (int i = 0; i < n; i += k << 1) {
for (int j = 0; j < k; j ++ ) {
int tmp = Gk[j] * f[i | j | k] % mod;
f[i | j | k] = f[i | j] + mod - tmp;
f[i | j] += tmp;
}
}
if (k == (1 << 10)) for (int i = 0; i < n; i ++ ) f[i] %= mod;
}
if (~op) for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod;
else {
int invn = qpow(n);
for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod * invn % mod;
}
}
void px(int *f, int *g, int n) {
for (int i = 0; i < n; i ++ ) f[i] = 1ll * f[i] * g[i] % mod;
}
void covolution(vector<int> &f, vector<int> &g) {
static int b1[N << 1], b2[N << 1];
int len1 = f.size(), len2 = g.size();
int n; for (n = 1; n < len1 + len2 - 1; n <<= 1);
for (int i = 0; i < len1; i ++ ) b1[i] = f[i];
for (int i = 0; i < len2; i ++ ) b2[i] = g[i];
NTT(b1, 1, n); NTT(b2, 1, n);
px(b1, b2, n); NTT(b1, -1, n);
f.resize(len1 + len2 - 1);
for (int i = 0; i < len1 + len2 - 1; i ++ ) f[i] = b1[i];
clr(b1, n); clr(b2, n);
}
void Poly_qpow(vector<int> &a, int k) {
vector<int> res = {1};
while (k) {
if (k & 1) covolution(res, a);
covolution(a, a);
k >>= 1;
}
a = res;
}
int n, m, q, a[N], b[5], cnt[N];
string s, t;
int ans[N];
int add(int x, int y) {
return (x + y >= mod ? x + y - mod : x + y);
}
void solve() {
cin >> n >> m;
for (int i = 0; i < n; i ++ ) cin >> a[i], cnt[a[i]] ++ ;
for (int i = 0; i < m; i ++ ) cin >> b[i];
for (int i = 0; i < m; i ++ ) {
int k1 = 0, k2 = 0;
for (int j = 1; j < b[i]; j ++ ) {
if (cnt[j] > 1) k2 ++ ;
else if (cnt[j]) k1 ++ ;
}
vector<int> F = {1, 2}, G = {1, 2, 1};
Poly_qpow(F, k1); Poly_qpow(G, k2); covolution(F, G);
for (int j = 0; j < F.size(); j ++ ) ans[j + 1 + b[i]] = add(ans[j + 1 + b[i]], F[j]);
}
cin >> q;
for (int i = 0, L; i < q; i ++ ) {
cin >> L;
cout << ans[L >> 1] << "\n";
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
// cin >> T;
while (T -- ) solve();
return 0;
}
CF1613F Tree Coloring
You are given a rooted tree consisting of $ n $ vertices numbered from $ 1 $ to $ n $ . The root of the tree is the vertex $ 1 $ .
You have to color all vertices of the tree into $ n $ colors (also numbered from $ 1 $ to $ n $ ) so that there is exactly one vertex for each color. Let $ c_i $ be the color of vertex $ i $ , and $ p_i $ be the parent of vertex $ i $ in the rooted tree. The coloring is considered beautiful if there is no vertex $ k $ ( $ k > 1 $ ) such that $ c_k = c_{p_k} - 1 $ , i. e. no vertex such that its color is less than the color of its parent by exactly $ 1 $ .
Calculate the number of beautiful colorings, and print it modulo $ 998244353 $ .
Input
The first line contains one integer $ n $ ( $ 2 \le n \le 250000 $ ) — the number of vertices in the tree.
Then $ n-1 $ lines follow, the $ i $ -th line contains two integers $ x_i $ and $ y_i $ ( $ 1 \le x_i, y_i \le n $ ; $ x_i \ne y_i $ ) denoting an edge between the vertex $ x_i $ and the vertex $ y_i $ . These edges form a tree.
Output
Print one integer — the number of beautiful colorings, taken modulo $ 998244353 $ .
设至少有 \(k\) 个点不满足 \(c_i - c_{p_i} \neq 1\) 的方案数为 \(f_k\),剩余 \(n - k\) 个点可以任意排列,由容斥可得 \(Ans = \sum\limits_{i = 0}^{n - 1}(-1)^{i}(n - k)!f_i\),考虑求 \(f_i\),在树上枚举任意一点 \(u\),设其含有 \(s_u\) 个儿子,只能选择一个儿子与其构成不匹配对,因此其方案数为 \(s_u\),考虑生成函数 \(F_u(x) = 1 + s_ux\),对所有点的生成函数组合有
其 \(x^i\) 的系数表示恰好有 \(i\) 个不匹配对的方案数,至此整个题目仅需要使用分治 NTT 即可预处理出 \(f_i\),时间复杂度 \(O(n\log^2{n})\)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define ull unsigned long long
#define PII pair<ll, ll>
#define pb push_back
#define clr(f, n) memset(f, 0, sizeof(int) * (n))
#define cpy(f, g, n) memcpy(f, g, sizeof(int) * (n))
#define rev(f, n) reverse(f, f + (n))
const int N = 1.1e6 + 10, _G = 3, mod = 998244353;
ll qpow(ll a, ll k = mod - 2) {
ll res = 1;
while (k) {
if (k & 1) res = res * a % mod;
k >>= 1;
a = a * a % mod;
}
return res;
}
const int invG = qpow(_G);
int rev[N << 1], rev_len;
void rev_init(int n) {
if (rev_len == n) return;
for (int i = 0; i < n; i ++ ) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? n >> 1 : 0);
rev_len = n;
}
void NTT(int *g, int op, int n) {
rev_init(n);
static ull f[N << 1], Gk[N << 1] = {1};
for (int i = 0; i < n; i ++ ) f[i] = g[rev[i]];
for (int k = 1; k < n; k <<= 1) {
int G1 = qpow(~op ? _G : invG, (mod - 1) / (k << 1));
for (int i = 1; i < k; i ++ ) Gk[i] = Gk[i - 1] * G1 % mod;
for (int i = 0; i < n; i += k << 1) {
for (int j = 0; j < k; j ++ ) {
int tmp = Gk[j] * f[i | j | k] % mod;
f[i | j | k] = f[i | j] + mod - tmp;
f[i | j] += tmp;
}
}
if (k == (1 << 10)) for (int i = 0; i < n; i ++ ) f[i] %= mod;
}
if (~op) for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod;
else {
int invn = qpow(n);
for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod * invn % mod;
}
}
void px(int *f, int *g, int n) {
for (int i = 0; i < n; i ++ ) f[i] = 1ll * f[i] * g[i] % mod;
}
void covolution(vector<int> &f, vector<int> &g) {
static int b1[N << 1], b2[N << 1];
int len1 = f.size(), len2 = g.size();
int n; for (n = 1; n < len1 + len2 - 1; n <<= 1);
for (int i = 0; i < len1; i ++ ) b1[i] = f[i];
for (int i = 0; i < len2; i ++ ) b2[i] = g[i];
NTT(b1, 1, n); NTT(b2, 1, n);
px(b1, b2, n); NTT(b1, -1, n);
f.resize(len1 + len2 - 1);
for (int i = 0; i < len1 + len2 - 1; i ++ ) f[i] = b1[i];
clr(b1, n); clr(b2, n);
}
int n, ans;
vector<int> edge[N];
vector<int> F[N];
int add(int x, int y) {
return (x + y >= mod ? x + y - mod : x + y);
}
int del(int x, int y) {
return x - y < 0 ? x - y + mod : x - y;
}
void calc(int l, int r) {
if (l == r) return;
int mid = l + r >> 1;
calc(l, mid); calc(mid + 1, r);
covolution(F[l], F[mid + 1]);
}
void solve() {
cin >> n;
for (int i = 1; i < n; i ++ ) {
int a, b;
cin >> a >> b;
edge[a].pb(b), edge[b].pb(a);
}
for (int i = 1; i <= n; i ++ ) {
if (i == 1) F[i] = {1, edge[i].size()};
else F[i] = {1, edge[i].size() - 1};
}
calc(1, n);
vector<int> frac(n + 1, 1);
for (int i = 1; i <= n; i ++ ) frac[i] = 1ll * frac[i - 1] * i % mod;
for (int i = 0; i < n; i ++ ) {
if (i & 1) ans = del(ans, 1ll * F[1][i] * frac[n - i] % mod);
else ans = add(ans, 1ll * F[1][i] * frac[n - i] % mod);
}
cout << ans << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
// cin >> T;
while (T -- ) solve();
return 0;
}
Mixing Colors



考虑黄色可能什么时候出现,当且仅当红色和绿色覆盖同一个点时贡献黄色,那么我们可以通过 红、绿、黄(R, G, Y) 集合的容斥得出
得到黄色点个数,进而知道所有颜色的个数,考虑一个颜色如何求解,我们分到 横、纵、斜(row, col, diag) 三个方向考虑横和纵的交非常容易处理,我们容易知道横纵的并是 \(n \times \text{row} + n \times \text{col} - \text{row} \times \text{col}\),较难处理的是斜线与两直线交的部分。
-
斜线与横线相交:对于一条斜线 \(x + y = k\),我们具有若干纵线 \(y = t\),横线会覆盖到的点是 \((1 \sim N, \, t)\),这告诉我们对 \(k\) 求前缀和,能产生交的斜线的 \(k\) 满足 \(t < k \le n + t\),可以 \(O(n)\) 枚举计算。
-
斜线与竖线相交,本质和上面那种情况一致,没有区别。
-
三条线交于一点,这是最难处理的情况,不过还好,我们有一种优秀的做法,由于横线和竖线覆盖了某一固定的 \(x\) 与 \(y\),因此我们可以通过卷积求出 \(x + y\) 的可达性,再依次检查每一条斜线是否满足经过 \((x, \, y)\)。
我们处理出所有的可能性之后,一种颜色所覆盖的点的个数可以确定:
然后分别对 \(R, \, G, \, R \cup G\) 求一次容斥就可以解决红绿黄点的个数,空点的个数等于总点数减去带颜色的点数,时间复杂度 \(O(n\log{n})\)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define ull unsigned long long
#define PII pair<ll, ll>
#define pb push_back
#define clr(f, n) memset(f, 0, sizeof(int) * (n))
#define cpy(f, g, n) memcpy(f, g, sizeof(int) * (n))
#define rev(f, n) reverse(f, f + (n))
const int N = 1.1e6 + 10, _G = 3, mod = 998244353;
ll qpow(ll a, ll k = mod - 2) {
ll res = 1;
while (k) {
if (k & 1) res = res * a % mod;
k >>= 1;
a = a * a % mod;
}
return res;
}
const int invG = qpow(_G);
int rev[N << 1], rev_len;
void rev_init(int n) {
if (rev_len == n) return;
for (int i = 0; i < n; i ++ ) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? n >> 1 : 0);
rev_len = n;
}
void NTT(int *g, int op, int n) {
rev_init(n);
static ull f[N << 1], Gk[N << 1] = {1};
for (int i = 0; i < n; i ++ ) f[i] = g[rev[i]];
for (int k = 1; k < n; k <<= 1) {
int G1 = qpow(~op ? _G : invG, (mod - 1) / (k << 1));
for (int i = 1; i < k; i ++ ) Gk[i] = Gk[i - 1] * G1 % mod;
for (int i = 0; i < n; i += k << 1) {
for (int j = 0; j < k; j ++ ) {
int tmp = Gk[j] * f[i | j | k] % mod;
f[i | j | k] = f[i | j] + mod - tmp;
f[i | j] += tmp;
}
}
if (k == (1 << 10)) for (int i = 0; i < n; i ++ ) f[i] %= mod;
}
if (~op) for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod;
else {
int invn = qpow(n);
for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod * invn % mod;
}
}
void px(int *f, int *g, int n) {
for (int i = 0; i < n; i ++ ) f[i] = 1ll * f[i] * g[i] % mod;
}
void covolution(int *f, int *g, int len, int lim) {
static int sav[N << 1];
int n; for (n = 1; n < len << 1; n <<= 1);
clr(sav, n); cpy(sav, g, n);
NTT(sav, 1, n); NTT(f, 1, n);
px(f, sav, n); NTT(f, -1, n);
clr(f + lim, n - lim), clr(sav, n);
}
ll n, m;
vector<ll> line[3][3];
ll red, green, yellow;
int F[N << 1], G[N << 1];
ll calc(vector<ll> *line) {
ll row = line[0].size(), col = line[1].size(), diag = line[2].size();
ll res = (row + col) * n - row * col;
vector<int> pre((n << 1) + 1);
for (int i = 0; i < diag; i ++ ) {
res += min(line[2][i] - 1, (n << 1) - line[2][i] + 1);
pre[line[2][i]] = 1;
}
for (int i = 1; i <= n << 1; i ++ ) pre[i] += pre[i - 1];
for (int i = 0; i < row; i ++ ) res -= pre[line[0][i] + n] - pre[line[0][i]];
for (int i = 0; i < col; i ++ ) res -= pre[line[1][i] + n] - pre[line[1][i]];
for (int i = 0; i < row; i ++ ) F[line[0][i]] = 1;
for (int i = 0; i < col; i ++ ) G[line[1][i]] = 1;
covolution(F, G, n + 1, (n << 1) + 1);
for (int i = 0; i < diag; i ++ ) res += F[line[2][i]];
clr(F, (n << 1) + 1); clr(G, n + 1);
return res;
}
void solve() {
cin >> n >> m;
for (int i = 0; i < m; i ++ ) {
int type, idx, color;
cin >> type >> idx >> color;
line[color ^ 1][type - 1].pb(idx);
line[2][type - 1].pb(idx);
}
for (int i = 0; i < 3; i ++ ) {
for (int j = 0; j < 3; j ++ ) {
sort(line[i][j].begin(), line[i][j].end());
line[i][j].erase(unique(line[i][j].begin(), line[i][j].end()), line[i][j].end());
}
}
red = calc(line[0]);
green = calc(line[1]);
yellow = red + green - calc(line[2]);
red -= yellow, green -= yellow;
cout << n * n - red - green - yellow << " " << red << " " << green << " " << yellow << "\n";
}
/*
5 10
2 4 1
3 3 1
2 1 1
3 7 0
1 3 1
3 3 0
3 8 0
1 5 0
2 4 1
2 2 0
*/
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
// cin >> T;
while (T -- ) solve();
return 0;
}
CF286E Ladies' Shop
A ladies' shop has recently opened in the city of Ultima Thule. To get ready for the opening, the shop bought $ n $ bags. Each bag is characterised by the total weight $ a_{i} $ of the items you can put there. The weird thing is, you cannot use these bags to put a set of items with the total weight strictly less than $ a_{i} $ . However the weights of the items that will be sold in the shop haven't yet been defined. That's what you should determine right now.
Your task is to find the set of the items' weights $ p_{1},p_{2},...,p_{k} $ $ (1<=p_{1}<p_{2}<...<p_{k}) $ , such that:
- Any bag will be used. That is, for any $ i $ $ (1<=i<=n) $ there will be such set of items that their total weight will equal $ a_{i} $ . We assume that there is the infinite number of items of any weight. You can put multiple items of the same weight in one bag.
- For any set of items that have total weight less than or equal to $ m $ , there is a bag into which you can put this set. Similarly, a set of items can contain multiple items of the same weight.
- Of all sets of the items' weights that satisfy points 1 and 2, find the set with the minimum number of weights. In other words, value $ k $ should be as small as possible.
Find and print the required set.
Input
The first line contains space-separated integers $ n $ and $ m $ ( $ 1<=n,m<=10^{6} $ ). The second line contains $ n $ distinct space-separated integers $ a_{1},a_{2},...,a_{n} $ ( $ 1<=a_{1}<a_{2}<...<a_{n}<=m $ ) — the bags' weight limits.
Output
In the first line print "NO" (without the quotes) if there isn't set $ p_{i} $ , that would meet the conditions.
Otherwise, in the first line print "YES" (without the quotes), in the second line print an integer $ k $ (showing how many numbers are in the suitable set with the minimum number of weights), in the third line print $ k $ space-separated integers $ p_{1},p_{2},...,p_{k} $ $ (1<=p_{1}<p_{2}<...<p_{k}) $ . If there are multiple solutions, print any of them.
Translation
给出 \(n\) 个不同的数 \(a_1, \ldots, a_n\) 现在要求从这 \(n\) 个数中选出最少的数字, 使得其满足每一个 \(a_i\) 都可以通过从中选取任意数字(每种数字可以选任意个)组成, 且从中取任意数字, 只要其和不超过 \(m\), 那么其和必然在之前的 \(n\) 个数里出现过。
乱搞
考虑贪心,最小的数一定会被选,那么它所能凑出来的数的和小于 \(m\) 的部分都需要在集合中,如果有个数不存在,那么一定无解,如果存在,就把这些数删去,然后接着判断,为了计算能凑出来的数,我们做一次卷积,将原覆盖函数 \(F(x)\) 与新数 \(k\) 的生成函数 \(G(x) = 1 + x^k + x^{2k} + \cdots\)(系数最高不超过 \(m\))每次卷积覆盖的数是原来的 \(\frac{m}{k}\) 倍,因此有价值的卷积最多只有 \(\log{m}\) 次,对于 \(2k > m\) 的数,其所覆盖的数我们不做卷积,直接把它与当前覆盖数之和小于等于 \(m\) 的拿出来枚举,复杂度可近似估计为 \(O(n)\),考虑 \(n\) 与 \(m\) 同阶,所以总时间复杂度 \(O(n\log^2{n})\)。
\(n\log^2{n}\) 打 \(n = 1e6\),真的假的?虽然是 8s 时限,但是还是没敢写,研究一下正解。
正解
考虑一个什么样的集合 \(T\) 满足其集合内元素任意组合能够构成 \(S\),设 \(f(T)\) 表示 \(T\) 集合在 \(m\) 以内的覆盖,其集合大小为 \(k\),显然必须满足 \(f(T) = S\),考虑第一个元素 \(a_1\) 一定存在,且其所能覆盖的点满足 \(a_1 + \sum\limits_{i = 2}^k a_i\),容易知道 \(\sum\limits_{i = 2}^k a_i\) 也在集合 \(S\) 中,由此,我们可以判断出,\(S\) 如果存在合法的集合 \(T\),那么一定存在两个数 \(a_i, \, a_j \in S\) 使得 \(a_i + a_j \in S\),我们可以通过一次卷积判断是否有解。
对于构造,我们考虑卷积告诉我们的信息,对 \(b_k\),如果存在两个数 \(a_i + a_j = b_k\) 那么这个数就不是必须的,如果这个数不能被表示出来,那么这个数就是一个必选的数,时间复杂度 \(O(m\log{m})\)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define ull unsigned long long
#define PII pair<ll, ll>
#define pb push_back
#define clr(f, n) memset(f, 0, sizeof(int) * (n))
#define cpy(f, g, n) memcpy(f, g, sizeof(int) * (n))
#define rev(f, n) reverse(f, f + (n))
const int N = 1.5e6 + 10, _G = 3, mod = 998244353;
ll qpow(ll a, ll k = mod - 2) {
ll res = 1;
while (k) {
if (k & 1) res = res * a % mod;
k >>= 1;
a = a * a % mod;
}
return res;
}
const int invG = qpow(_G);
int rev[N << 1], rev_len;
void rev_init(int n) {
if (rev_len == n) return;
for (int i = 0; i < n; i ++ ) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? n >> 1 : 0);
rev_len = n;
}
void NTT(int *g, int op, int n) {
rev_init(n);
static ull f[N << 1], Gk[N << 1] = {1};
for (int i = 0; i < n; i ++ ) f[i] = g[rev[i]];
for (int k = 1; k < n; k <<= 1) {
int G1 = qpow(~op ? _G : invG, (mod - 1) / (k << 1));
for (int i = 1; i < k; i ++ ) Gk[i] = Gk[i - 1] * G1 % mod;
for (int i = 0; i < n; i += k << 1) {
for (int j = 0; j < k; j ++ ) {
int tmp = Gk[j] * f[i | j | k] % mod;
f[i | j | k] = f[i | j] + mod - tmp;
f[i | j] += tmp;
}
}
if (k == (1 << 10)) for (int i = 0; i < n; i ++ ) f[i] %= mod;
}
if (~op) for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod;
else {
int invn = qpow(n);
for (int i = 0; i < n; i ++ ) g[i] = f[i] % mod * invn % mod;
}
}
void px(int *f, int *g, int n) {
for (int i = 0; i < n; i ++ ) f[i] = 1ll * f[i] * g[i] % mod;
}
void covolution(int *f, int *g, int len, int lim) {
static int sav[N << 1];
int n; for (n = 1; n < len << 1; n <<= 1);
clr(sav, n); cpy(sav, g, n);
NTT(sav, 1, n); NTT(f, 1, n);
px(f, sav, n); NTT(f, -1, n);
clr(f + lim, n - lim), clr(sav, n);
}
int n, m, a[N], cnt[N];
int F[N << 1];
void solve() {
cin >> n >> m;
for (int i = 0; i < n; i ++ ) cin >> a[i], cnt[a[i]] = F[a[i]] = 1;
covolution(F, F, m + 1, m + 1);
for (int i = 0; i <= m; i ++ ) if (F[i] && !cnt[i]) return cout << "NO\n", void();
cout << "YES\n";
vector<int> ans;
for (int i = 0; i < n; i ++ ) if (!F[a[i]]) ans.pb(a[i]);
cout << ans.size() << "\n";
for (int i = 0; i < ans.size(); i ++ ) cout << ans[i] << " ";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
// cin >> T;
while (T -- ) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号