OO第一单元作业总结

OO第一单元作业总结

一、基于度量分析程序结构

1. 第一次作业

架构分析

第一次作业相对简单，个人感觉更多的是在考察java的基础语法，对面向对象的考察并不多。考虑到整个式子只会有系数和指数作为因子，我决定把这两者合并为一个因子。建立Item类，其中同时包括系数与指数。正则表达式匹配出每个item，然后建立item，factor对自身包含的若干个item进行相乘，也就是系数相乘指数相加。这样做之后，求导和化简就显得方便了很多。只需要对每个factor进行求导然后再expression里对每个factor进行判断是否可以合并就行。

本项目包含四个类，分别如下：

1. MainCLass 主类，完成字符串的输入输出，调用Expression完成相关工作
2. Expression：表达式类，通过表达式字符串，解析，创建包含若干个factor的存储结构，并支持求导操作和对Item的合并
3. Item：传入字符串，合并若干Factor，支持求导操作
4. Factor：通过字符串创建整个表达式的最基本单位：因子。

以下是类图

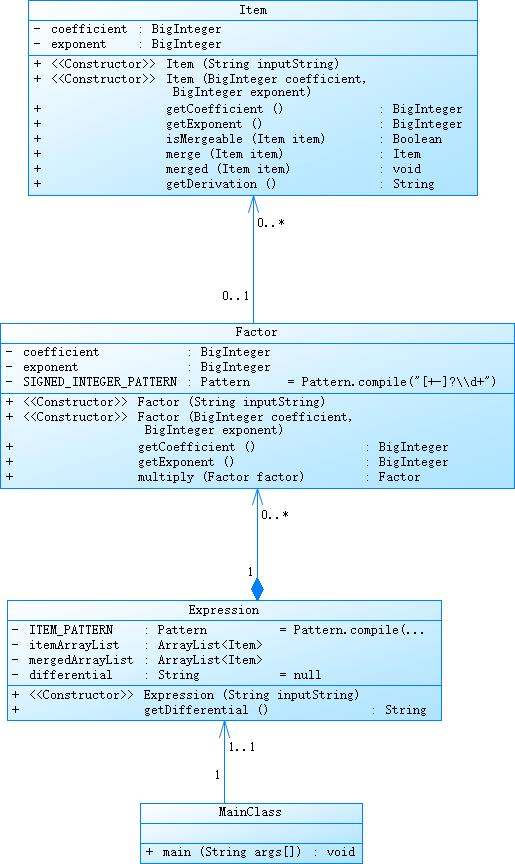
度量分析

class	属性个数	方法个数	代码规模（行）
MainClass	0	1	9
Expression	4	2	71
Factor	3	5	92
Item	3	5	43

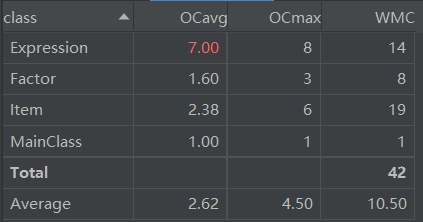
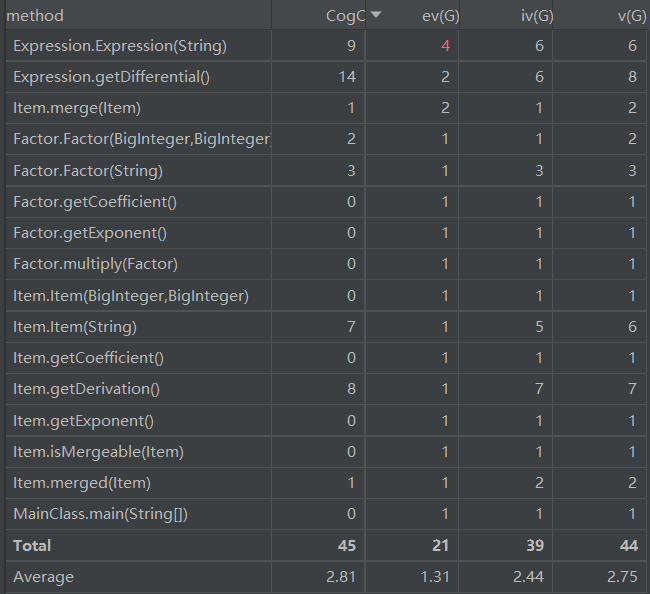
整体分析

优点：

• 结构比较简单，抓住了最基础的存储结构
• 无bug，化简到了最简

缺点：

• 缺少面向对象思想，单一Item的编程方法注定了可扩展性极差
• 没有采用工厂模式，导致Expression的构造函数的复杂度有些高
• Item和Factor功能高度重合

2. 第二次作业

第一次作业糟糕的结构注定了本次作业的重构。

第二次作业与第一次相比的结构上的重大改进在于：

1. 增加了三角函数类，表达式因子类
2. 实现了求导接口，每个需要求导的类只需要实现Formula接口即可，初步实现了多态
3. 采用梯度下降算法

架构分析

本项目共有9个类：

1. MainClass： 完成输入输出操作
2. Expression：表达式，输入字符串构建，采用梯度下降把处理任务分解交给Fatcor。其内部存储了若干Factor的引用，用以表示一个Expression是由若干项相加得到。实现了求导接口。
3. Factor：项。输入字符串，采用短正则匹配把字符串拆成好几个因子，任务交给因子，实现求导接口
4. ConstFactor： 有符号常数因子
5. ExponentFactor：幂函数银子
6. Triangle：三角函数因子
7. Sine：继承Triangle
8. Cosine：继承Triangle

类图如下：

度量分析

class	属性个数	方法个数	代码规模（行）
MainClass	0	2	28
Expression	1	14	218
Item	16	31	562
ConstFactor	0	11	51
Cosine	0	9	51
Sine	0	9	52
ExponentFactor	1	9	69
Triangle	1	10	70
Formula	0	1	3

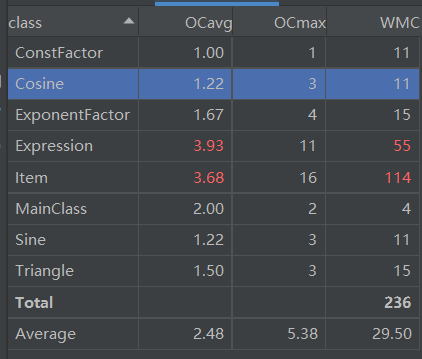
整体分析

从上图可以看到，本次作业的代码复杂夫太高，主要因为Expression和Item类内部的运算过于复杂。具体原因如下：

1. 梯度下降算法把过多的解析工作交给了Item，导致Item在解析表达式就很复杂，产生了两百多行的代码
2. 化简过程十分复杂，支持项与项的加减法合并，因子与因子的乘法合并，三角函数的化简，去除括号。
3. 实现的大量方法中有部分功能重叠
4. ConstFatcor类的所有方法完全继承BigInteger，显得这个类十分多余

3. 第三次作业

架构分析

本次作业充分发挥了不同因子之间的继承关系，根据不同因子之间的相似功能，自下而上的确立了继承关系，结果如下：

1. MainClass：主类，完成输入输出
2. Item：项类，存储系数与Factor List
3. Expression：表达式，内部存储Factor List， 继承Factor
4. Factor：因子抽象类
5. Exponent：含有指数函数的类，内部存放指数，继承Factor
6. Power：幂函数类，继承Exponent
7. Triangle：三角函数类，继承Exponent
8. Sine：正弦三角函数类，继承Triangle
9. Cosine：余弦三角函数类，继承Triangle
10. Constant: 常数类
11. FactorFactory：因子工厂，利用梯度下降算法不断解析产生不同类别的因子

类图如下：

度量分析

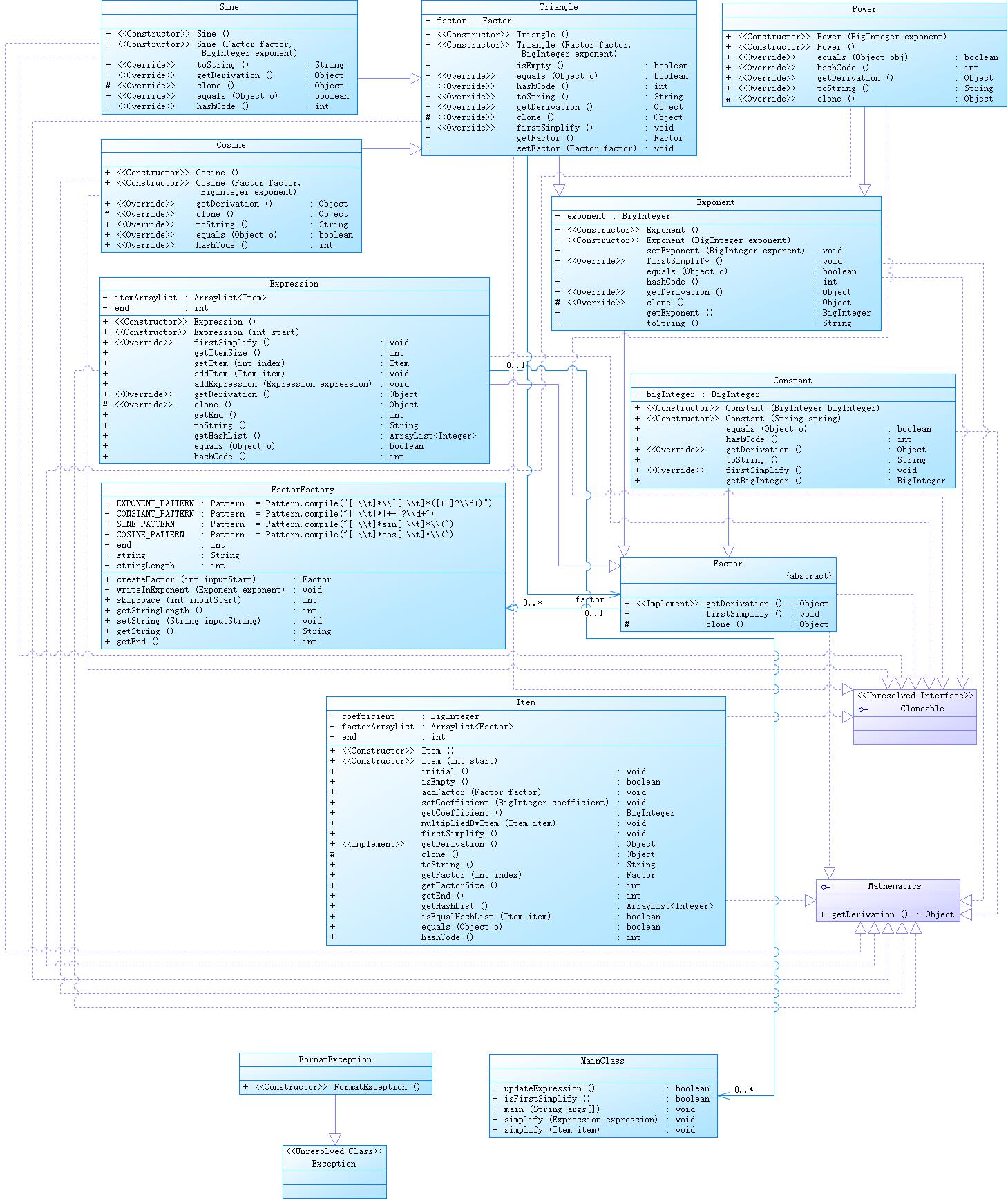
整体分析

class	属性个数	方法个数	代码规模（行）
MainClass	0	5	63
Item	3	19	236
Expression	2	14	171
Factor	0	3	12
Exponent	1	10	71
Power	0	7	45
Triangle	1	11	94
Sine	0	7	55
Cosine	0	7	53
Constant	1	8	52
FactorFactory	7	7	113
Mathematics	0	1	3
FormatException	0	1	5

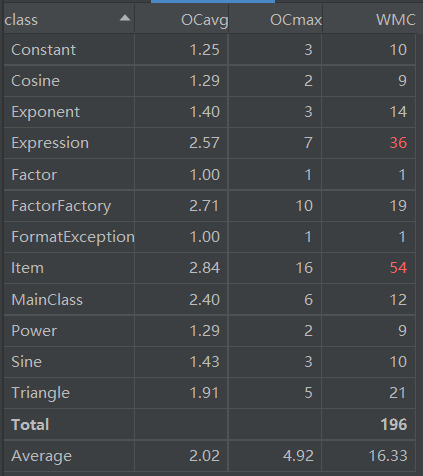
整体分析：

上图可以看到，本次任务虽然问题更加复杂，但是代码的复杂度反而比第二次作业下降了。一是因为化简操作没有上次那么狠了，此次化简就没有对三角函数进行。二也是因为这采用了工厂模式，把生成类的工作交给了FactorFactory，简化了Item的构造函数。

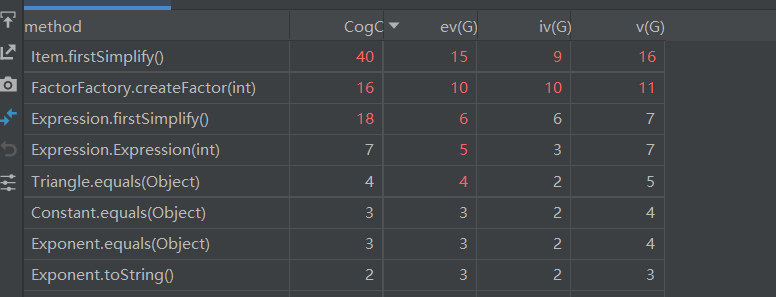
从这张对方法进行分析的图中也可以看出，目前代码的复杂度和耦合度主要集中在了化简和工厂内部，如果有下次作业可以考虑采用工厂模式进行化简。

bug分析

三次作业强测均无bug，第二三次作业互测的bug为：

• 第二次：测试时候为了适配本地自己搭建的评测机，对输入数据进行了限制，不符合就会强行return，提交的时候忘记删除了；如果输出为0则会输出为空字符串
• 第三次：存在一种情况输出的时候删除括号，只删了左半边忘删右半边了

发现bug策略

第一次作业我才用的策略就是通过自己搭建的评测机生成大量测试数据，然后使用python的subprocess库自动调用别人的java程序进行测试，然后使用sympy库进行评测对比。这种方法好处在于方便简单，只需要程序一直跑就可以，找到就是赚到，找不到也不耽误自己时间。但这种方法的问题在于，我们写程序，通常的bug发生在数据集的“边界位置”，正常的样例大家一般都不会有错的。毕竟都是通过中测的人了。但是评测机自动生成的数据一下子几百条，其背后很可能都属于几个大的数据类别，对于很边缘的数据是很难覆盖到的。而且随着规则限制的增加，这种情况愈发明显。

于是在第二次作业中，我一方面改进了评测机，支持对runtime error和TLE的判断，并且对jar文件进行评测能够提升平测速度。但同时我采用机器生成与手动生成数据相结合的办法，成功hack到了2个人。

第三次作业，我依旧想延续第二次的方法，无奈整个屋子只有我被hack了。。。

唉，菜是原罪！

重构总结

在二、三次作业中，我都经历了重构，虽然重构是很浪费时间的，但我感觉，这对我代码能力还是有很大的提升的。

第一次->第二次

这次的重构基本可以属于迫不得已而为之。第一次作业因为第一次上手写大型java项目（其实很小），没有在整体结构上过的的考虑，除了主类只有三个类，几乎没有可扩展性。而且第一次作业因为不存在递归嵌套的问题，我用一种“最简单元”的的方式去解决。认为式子一定可以分解为若干个同类型的最简单元相加。显然这种想法到了第二次作业就行不通了。于是第二次作业中，我增加了类的数量，但整体结构没有大的改变，还是有一些代码能够直接copy第一次作业的。

第二次->第三次

其实第二次作业到第三次作业也并非一定要经历重构。但是第二次作业的结构依然不符合老师推荐的最佳结构。于是第三次作业，我经历了从头到尾的重构。在第三次作业中，我运用了大量的继承关系，减少了整体的代码量。例如sin和cos的括号里都有因子，于是我就建立了公共父类Triangle来管理他们的公共部分。sin和cos的求导只需要在Triangle求导的基础上进行操作即可。同理Triangle和Power都有指数，于是建立了父类Exponent来管理这个参数。此外，为了增加程序的可扩展性，对于所有的因子，都继承了Factor的抽象类，实现了求导接口。另外运用工厂模式进行梯度下降算法，让我的代码可读性上升了许多。

经历了这次重构，虽然执行的功能变多了，但是代码复杂度反而下降了许多，可读性也有了很大的提升。

心得体会

总的来说，我感觉经历了这三次磨练，我的代码能力有了很大的提升。更重要的是对整体结构的规划能力和面向对象思想的把握变好了。从第一次到第三次，可以说是写程序越来越有面向对象的色彩，程序的可扩展性，鲁棒性越来越好。如果需要在第三次的基础上插入很多别的功能，比如tan、表达式赋予指数，我想应该不是一件难事了。

加油吧！虽然累但很有成就感！!