FWT妙题

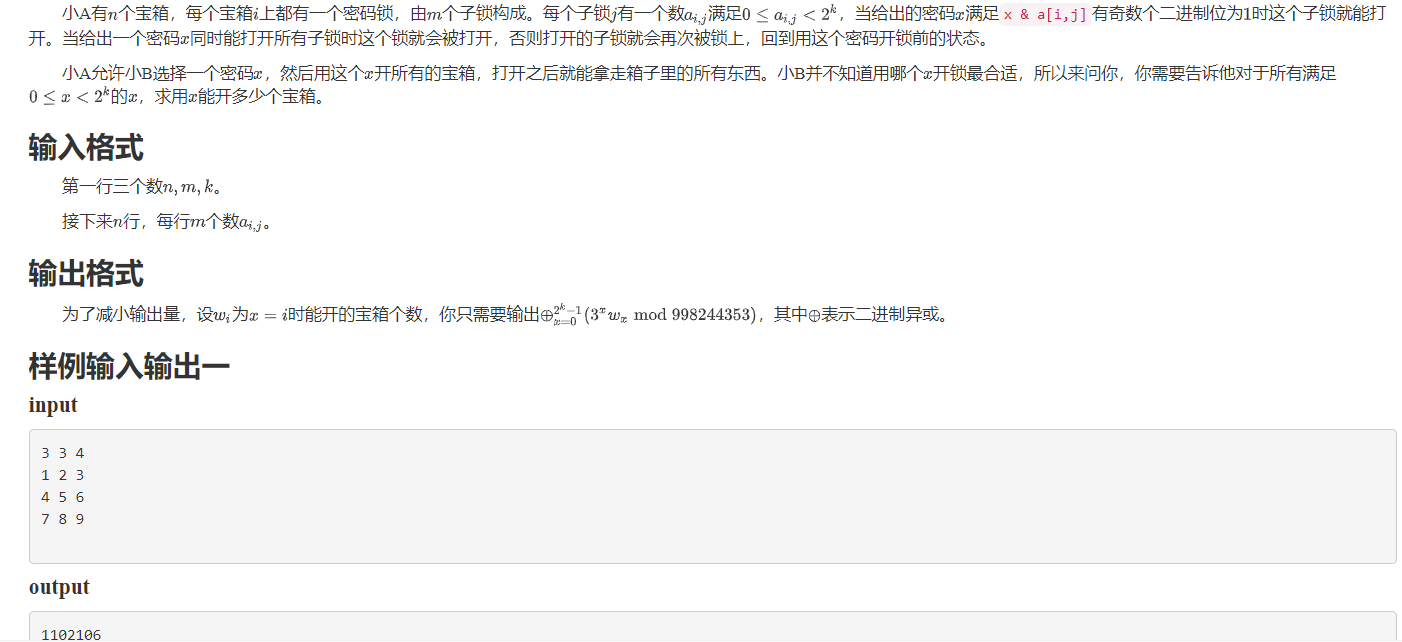
$$m = 1的情况下\\ FWT意义下，(-1)^{|S\oplus T|}为S-->T的贡献\\ 故ans_i = \frac{n - Fwt[i]}{2}\\ m大的情况\\ b_{i,S} = \oplus_{j \in S}a_{i,j}\\ c_{i,S} = (-1)^{|b_{i,S}\oplus X|}\\ 合法，仅当c_{i,S} = (-1)^{S}\\ \sum_{S}(-1)^{|S|}c_{i,S} = 2^m才合法\\ ans_x = \frac{1}{2^m}\sum_{S}(-1)^{|S|}(-1)^{|b_{i,S}\oplus X|}\\ ans_x = \frac{1}{2^m}\sum_{S}(-1)^{|S|}(-1)^{|b_{i,S}\oplus X|}\\ $$

直接插入一下$b_{i,s}$然后做个fwt就好了