高维生成函数
例子:
二维生成函数的形式幂级数:\(F = \sum_{i = 0}^n\sum_{j = 0}^ma_{i,j}x^iy^j\)
考虑对其卷积:
\[A * B = C = \sum_{i = 0}^{A_n}\sum_{i = 0}^{A_m}a_{i , j}x^iy^j\sum_{i = 0}^{B_n}\sum_{i = 0}^{B_m}b_{i , j}x^iy^j\\
\sum_{Cx_i = 0}^{A_n + B_n}\sum_{Cy_i = 0}^{A_m + B_m}x^{Cx_i}y^{Cx_i}\sum_{Ax_i + Bx_i = Cx_i}\sum_{Ay_j + By_j = Cx_j} (\frac{Cx_i}{Ax_i})(\frac{Cy_i}{Ay_i})a_{Ax_i,Ay_i}b_{Bx_i,By_i}
\]
上面的式子没什么用
经过一些推到有以下结论:
对各个维度单独做一个DFT,然后再相应点乘起来,最后再对每一个维度IDFT回去,便可以得到原卷积
对于二维:
可以先枚举第一维,然后对每一个第二维DFT
在上一维度的结构:再枚举第二维,然后对每一个第一维DFT一下
最后将点相应点乘起来最后再枚举第二维,然后对于每一个第一维IDFT
再枚举第一维,然后对每一个第二维IDFT一下
最后就是卷积答案
复杂度大概是\(O(n^mlogn)\)
更多的例子:FWT,FMT (本质上就是一个高维插值)
记号:
\[S = \sum_{i}s_i\\
\]
建出这样一张图:
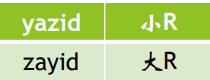
不妨将第一行人数设为一个维度\(x\),第一列人数设为第二个维度\(y\)
然后就有了一下这个矩形:
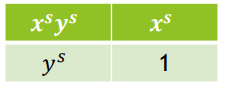
那么原题目的若干限制就可以表示为若干个\(x,y\)相关的区间
然后就是要求出相关的二元生成函数了
考虑对于每一个城市的学校\(\{s_1,s_2,...,s_l\}\)
每个学校要么选择第一行,要么选择第二行
\[容易列出如下式子:\\
\prod(x^{s_i}y^{s_i} + x^s) +\prod(y^{s_i} + 1)\\
即:
(\prod(x^{s_i} + 1) + 1)(\prod(y^{s_i} + 1))
\]
此时\(x,y\)分别独立
对于有限制的学校也一样这么做即可
生成函数杂题:
CF986D

首先有个显然的结论:
\[2至多出现两次\\
其余出现的只有3\\
感性证明:\\
4可以由两个2表示\\
5可以由3 + 2表示,且3 * 2 > 5\\
.
.
.
\]
分别枚举一下2的个数
然后预处理若干\(3^{2^k}\),
倍增一下就好了
倍增的时候可以看一下位数,就可以快速判断
卷积形式及其变形:
\[加卷积:C_i = \sum_{j + k = i}A_j B_k\\
直接正常卷积
\]
\[差卷积:C_i = \sum_{j - k = i}A_j B_k\\
取A'_{-j} = A'_{n-j} = A_j即可
\]
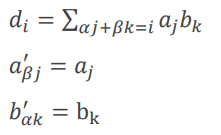
多项式位移:
给定一个n次多项式\(A(x),以及一个d\)
求\(B(x) = A(x + d)\)
\[A(x + d) = \sum_{i = 0}^n(x + d)^ia_i\\
=\sum_{i = 0}^na_id^i\sum_{j = 0}^i\binom{i}{j}x^{j}d^{-j}\\
=\sum_{i = 0}^na_i*i!\sum_{j = 0}^i\frac{x^j}{j!}\frac{d^{i-j}}{(i-j)!}\\
=\sum_{j = 0}^n\frac{x^j}{j!}\sum_{i = j}^na_i*i! \frac{d^{i-j}}{(i-j)!}\\
\]
卷卷就好了
比较基本就跳了
多项式求逆:
分治fft:
简单例子:
求某一行的第一类斯特林数:
\(S(n,k) = S(n - 1 , k - 1) + (n - 1)S(n -1 , k)\)
可以写出生成函数\(S_n = S_{n - 1} (x + n - 1)\)
简单的有\(S_n = x^{\overline{n}}\)
分治FFT可以做到\(O(nlog^2n)\)
但没什么必要
直接套用上面的分治FFT的时候,如果左右两边的项数相同则可以直接,多项式位移就可以做到\(O(nlogn)\)
多项式取模/除法
对于一个n次多项式\(A(x)\),以及一个m次多项式\(B(x)\),找到两个多项式\(Q(x),R(x)\),满足\(A(x) = B(x) * Q(x) + R(x)\) , 且\(R(x)的次数 < m\)
做法:
考虑一个操作\(rev(A(x))\)为前后调换\(A(x)\)的所有系数
\(rev(A(x)) = A(\frac{1}{x})x^n\)
\[A(x) = B(x)*Q(x) + R(x)\\
A(\frac{1}{x}) = B(\frac{1}{x})Q(\frac{1}{x}) + R(\frac{1}{x})\\
x^nA(\frac{1}{x})=B(\frac{1}{x})x^{m} Q(\frac{1}{x})x^{n-m} + R(\frac{1}{x})x^{m - 1} * x^{n-m+1}\\
有rev(A(x)) = rev(B(x)) * rev(Q(x)) + rev(R(x)) * x^{n-m + 1}\\
在模x^{n-m + 1}意义下\\
rev(A(x)) = rev(B(x)) * rev(Q(x)) \\
故rev(Q(x)) = \frac{rev(A(x))}{rev(B(x))}\\
求逆之后再反转一下系数就好了\\
R(x) = A(x) - B(x)Q(x)
\]
EGF
类比于OGF,EGF的位移是对生成函数进行微分/积分
常见的EGF
\[(1,1,...,1) = e^x\\
(1,-1,1,-1,...)=e^{-x}\\
(1,0,1,0,...)=\frac{e^x+e^{-x}}{2}
\]
\[([k|0] , [k|1] , [k|2]....[k|i])
\]
考虑单位根反演:
\[[n|k] = \frac{1}{n}\sum_{i = 0}^{n - 1}w_{n}^{ik}\\
简单证明:n|k时候,直接就是等于1的十分显然\\
n不能整除k的时候,[n|k] = \frac{1}{n}\frac{w^{nk}{ - w_n^0}}{w_n^{k} - 1} = 0
\]
故上式可以写成:
\[\sum_{i =0}[x^{ik}]f(x) = \sum_{i}[k|i]x^ia_i = \sum_i a_i\frac{1}{k}\sum_{j = 0}^{k - 1}x^iw_k^{ji}\\
= \sum_{i = 0}^{n} a_i\frac{1}{k}\sum_{j = 0}^{k - 1}(xw_k^{j})^i\\
= \frac{1}{k}\sum_{j = 0}^{k - 1}\sum_{i = 0}^{n} a_ix^i(w_k^{j})^i\\
= \frac{1}{k}\sum_{j = 0}^{k - 1}f(w_k^j)\\
回到到e^x里\\
([k|0] , [k|1] , [k|2]....[k|i]) = \frac{1}{k}\sum_{j = 0}^{k - 1}e^{x * w^j_k}
\]
多项式ln,exp
exp是个体映射到集体
ln是集体映射到个体
OI意义下的微分方程求解
uoj50【UR#3】链式反应 - 大米饼 - 博客园 (cnblogs.com)

\(积性函数在乘法意义下是封闭的\)
这里有一些有意思的东西:
\[积性函数的和也是积性函数\\
积性函数的因数前缀和也是积性函数\\
(自证不难)
\]
即\(ans = \prod_{p_i,\sum v_i = N}F(p_i^{v_i})\)
\[F(p^{v_i}) = \sum_{\sum_{j = 1} i_j = v_i} \prod_{j}\varphi(p^{i_j})\\
考虑求出\phi(p_i)的生成函数\\
\varphi(p^i) = p^{i - 1}(p - 1)\\
1 , p - 1,(p-1)p,... , (p - 1)p^i\\
有: 1 + \frac{x(p_i - 1)}{1-p_ix} 可以写成形式\frac{A(x)}{B(x)}
\]
但发现\(N <= 10^9\)
考虑多项式次数只有\(m <= 10^5\)
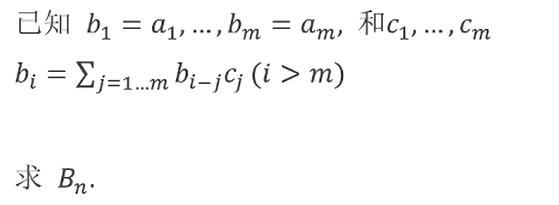
直接BM递推就好了
或者考虑最后的答案是个线性递推
也就是说,只用考虑率\(B_n\)的系数是多少
可以倍增n,然后对之前求出的m次多项式取模
最后复杂度就是\(O(mlognlogm)\)
#6275. 棋盘 - 题目 - LibreOJ (loj.ac)
有一个状压dp的做法
从左往右依次
\[f[i][S][j] = f[i - 1][T][k]\ \ \ [k + val(T , S) == j]
\]
最后一维长得很像一个背包
并且转移可以写成一个矩阵
于是原方程可以写成一个 多项式矩阵
考虑如何做多项式矩阵快速幂
考虑NTT过程,可以先带入n次单位根进去,然后再做一个矩阵快速幂
再对最后求出来的所有点值做一次IDFT,就可以了
考虑转移过程中,有一些状态是相似的,可以类似的转移
类似于维护这么一个矩阵
\[\begin{bmatrix}
1,x\\
x,x^2
\end{bmatrix}
\]
这道题就无了
拉格朗日差值
考虑经过n个点的拟合曲线的解析式:
\[\sum_{i = 1}^n y_i\prod_{j!=i}\frac{(x-x_j)}{(x_i-x_j)}
\]
在OI中的应用:将某些dp方程归纳成一个若干次数的多项式,然后直接差值
例题:
机器人
斗主地
我不是很会吧
\[\sum_{i = 1}^ni^k式子的维护
\]
三种方法
1.伯努利数
2.转下降幂
3.点值爆艹
\[\sum_{i = 0}^nx^i\sum_{j = i}^nj^i\\
=\sum_{j = 0}^n\sum_{i = 0}^j x^ij^i\\
=\sum_{j = 0}^n\sum_{i = 0}^j (xj)^i\\
\]
直接等比一下就无了,感觉这个式子好奇怪,好像是我记错了
HDU 6796

有一个状压dp的做法
直接维护一个可重集,然后直接dp转移即可
也有 18 * 10 次EGF之积的做法



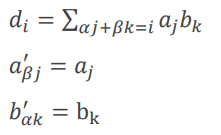

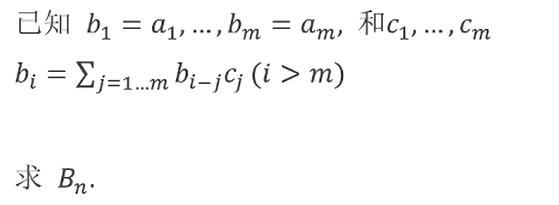




 浙公网安备 33010602011771号
浙公网安备 33010602011771号