21th Feb

【1】 二叉树的一些性质

https://www.jianshu.com/p/bce7efe8d45e

【2】 等比数列求和公式

 

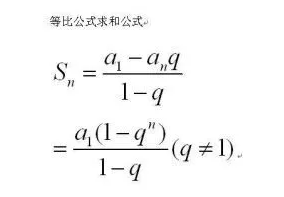
2^0 + 2^1 + 2^2 + 2^3 +...+ 2^n =  2^(n+1) - 1 ;

【3】

36节有序表

https://www.mashibing.com/study?courseNo=339&sectionNo=41462&systemId=21&activeIndex=0 

左旋后 搜索二叉树性质不变；

左旋原因，感觉 右树太大了；

 

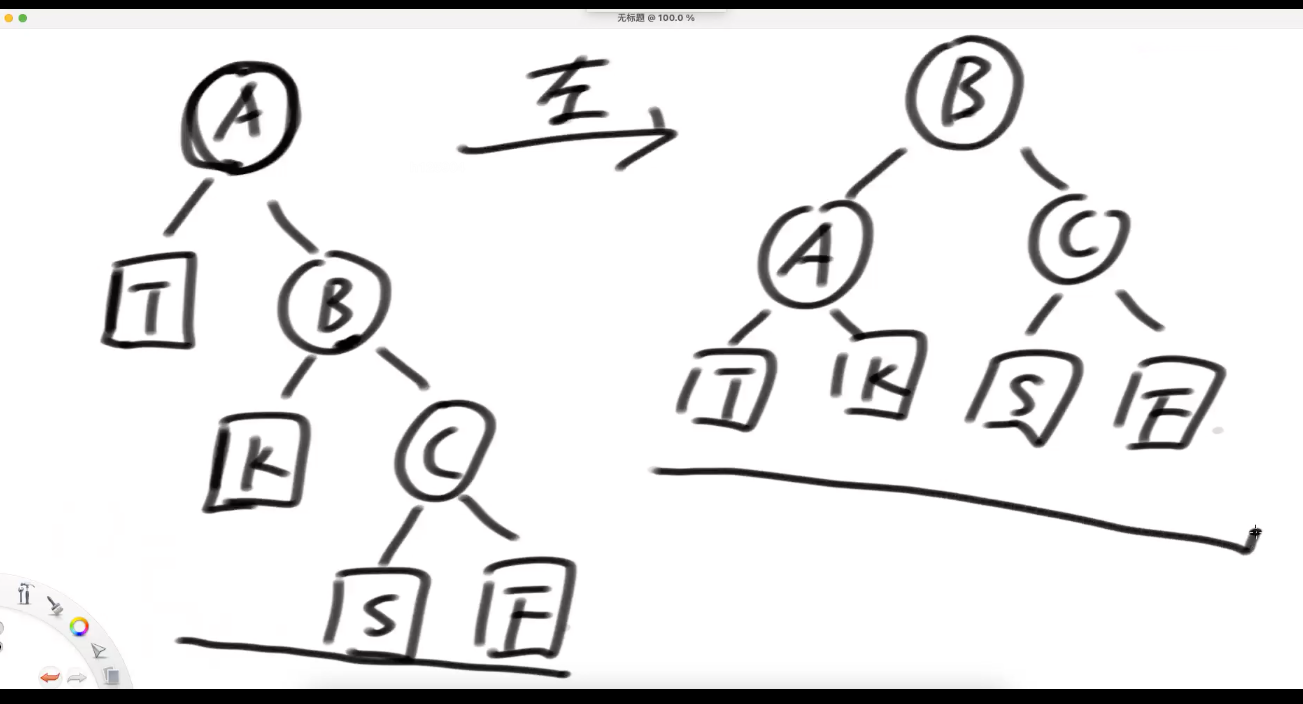
===》对应的 右旋

头结点 往哪边倒 就是什么旋

 

avl,sb树(Size balance tree)，红黑树==》 不管你是哪种 时间复杂度的量级都一样 LgN;

 

LL---》做右旋

 

 

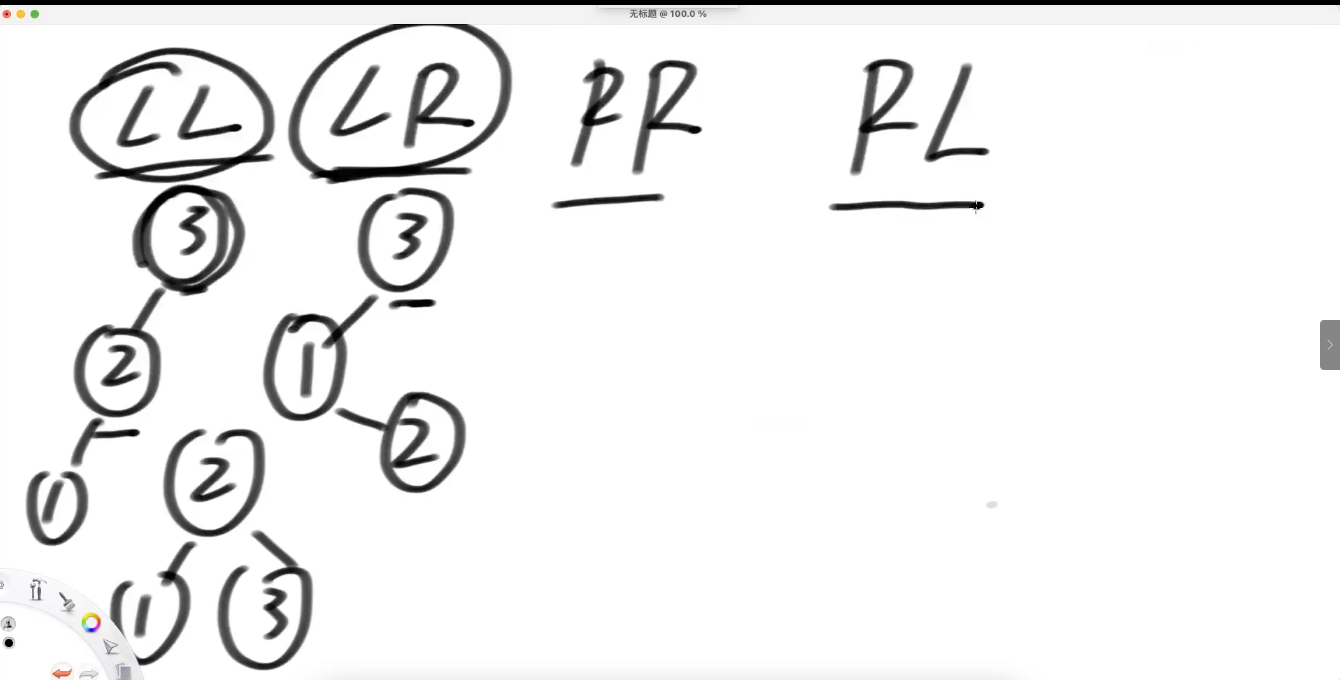
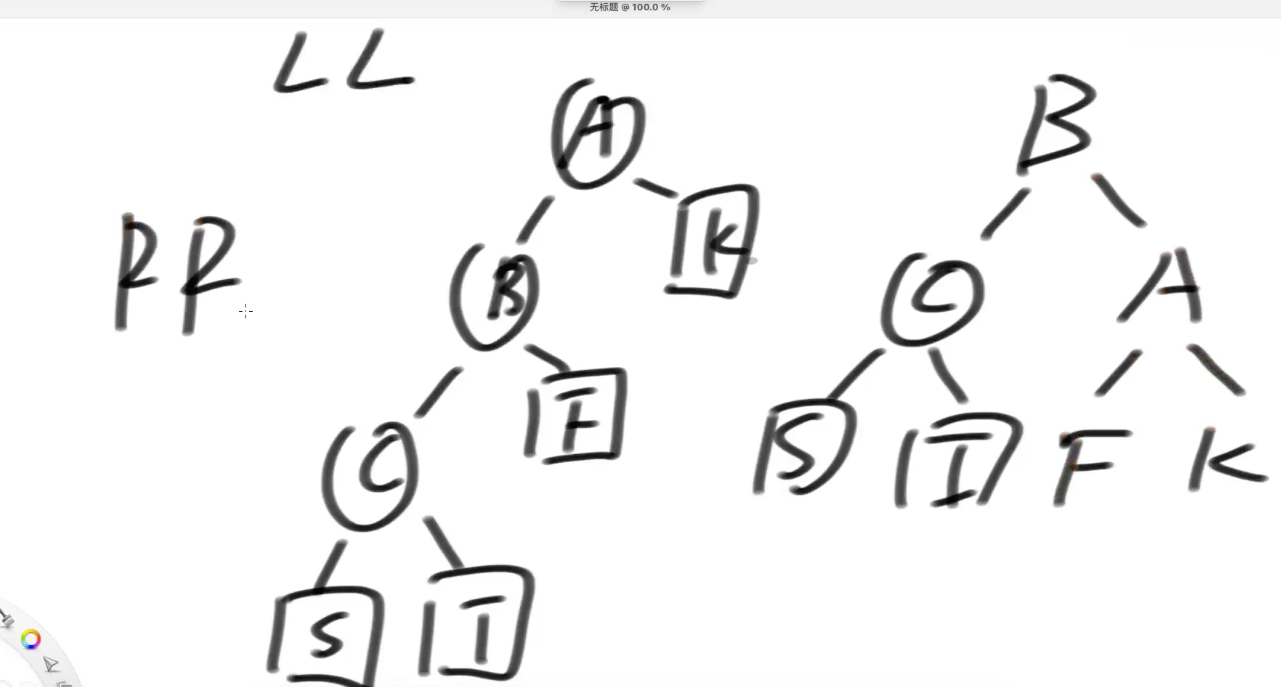
LR （根节点的 左树 比 右树 高 ； 再 具体看是 ---》 左树中的 右孩子树 过高导致的）===> 让孙子  

 

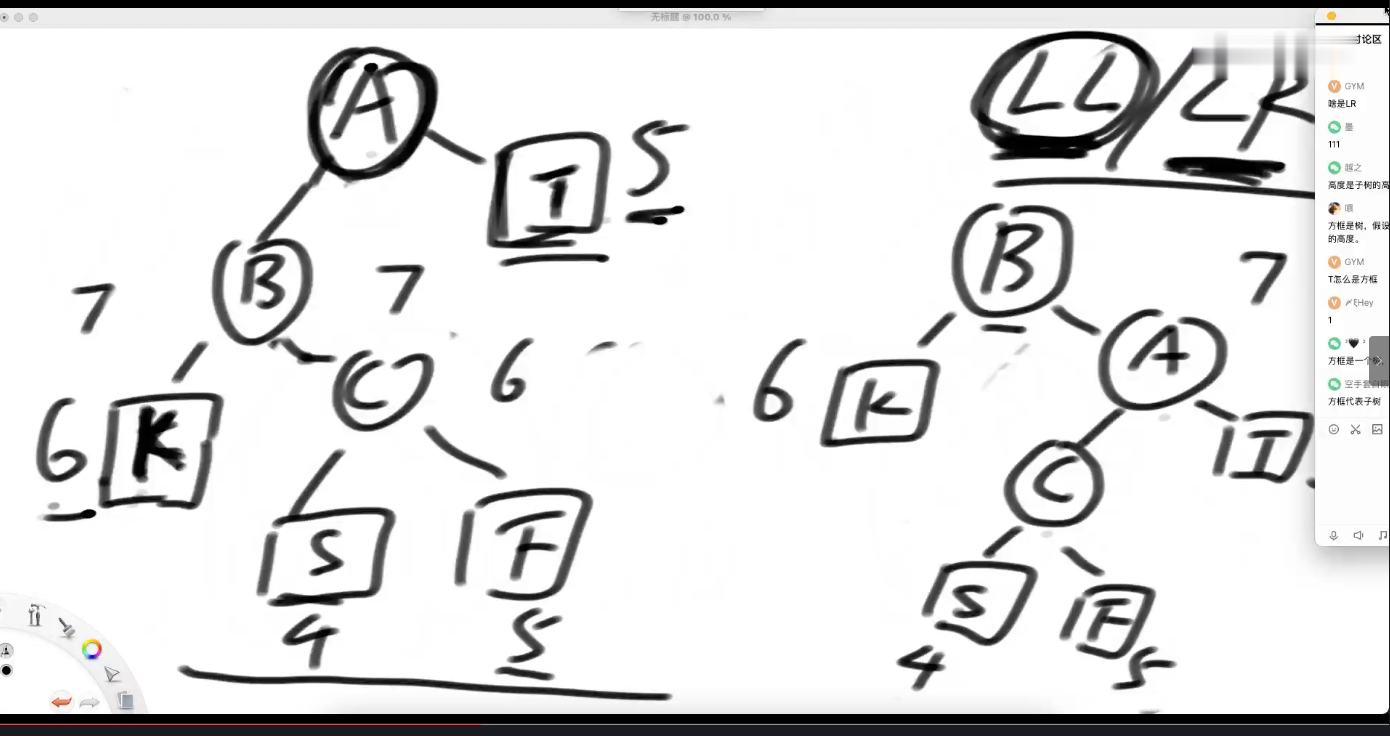
LR 型 调整策略 --目的---》想尽办法让C 去到 A的位置

---【1】 先在B节点 对B 来左旋

 

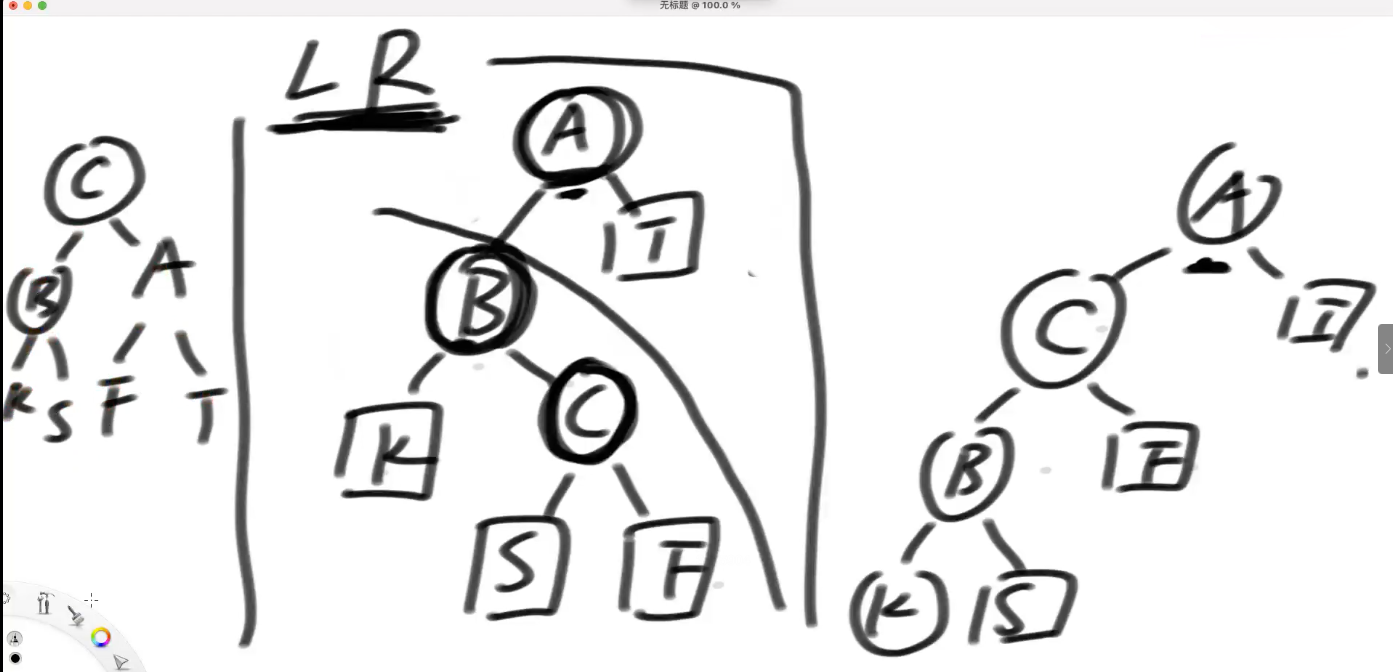
    【3】                           【1】                                           【2】

LR  -->  LL  -->  再去调 LL 递归

 

实例：

难调的一种

 

 

 

 

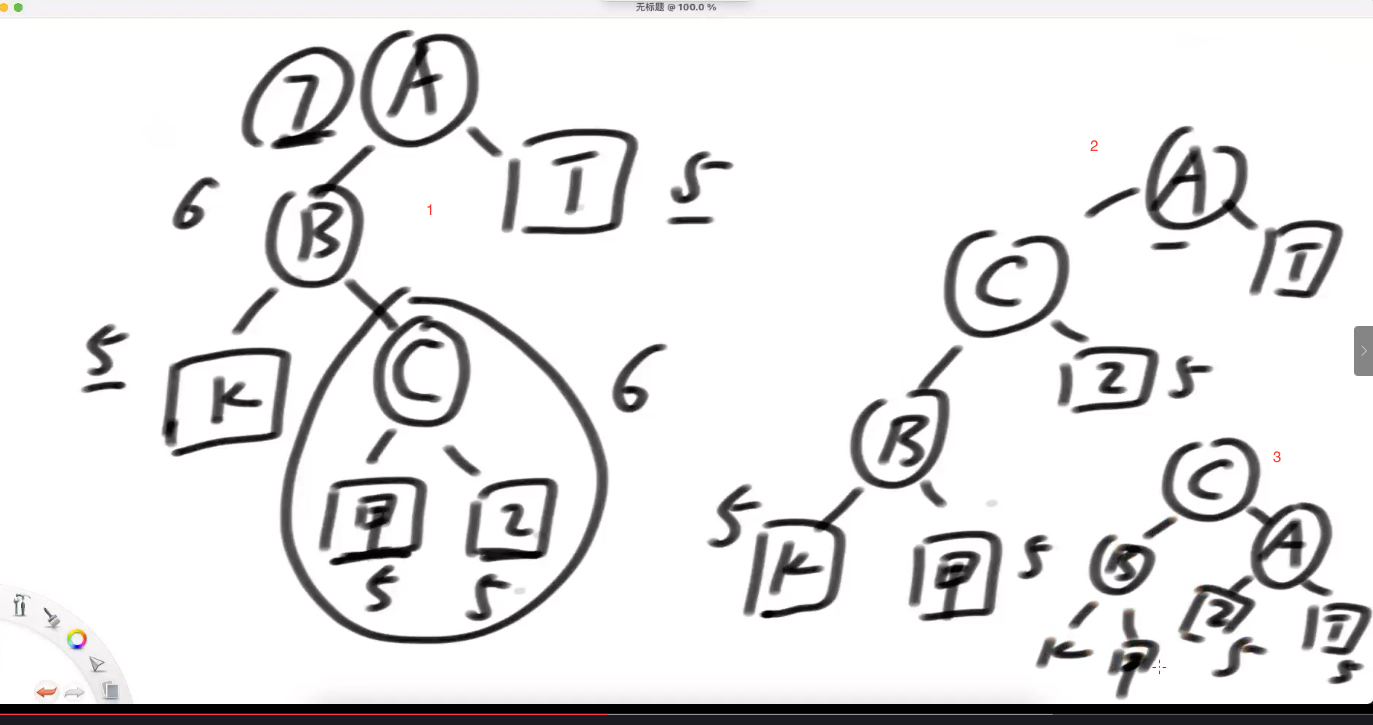
同理：rr型 做一步 左旋

 

RL  --> 变成 RR型 （异常高的左子树 的 根节点 做一次）---》再左旋一次

 

 

 

即是LL型违规·又是LR型违规；---》【仍旧 按照 LL 型 来调整】

 

 

 

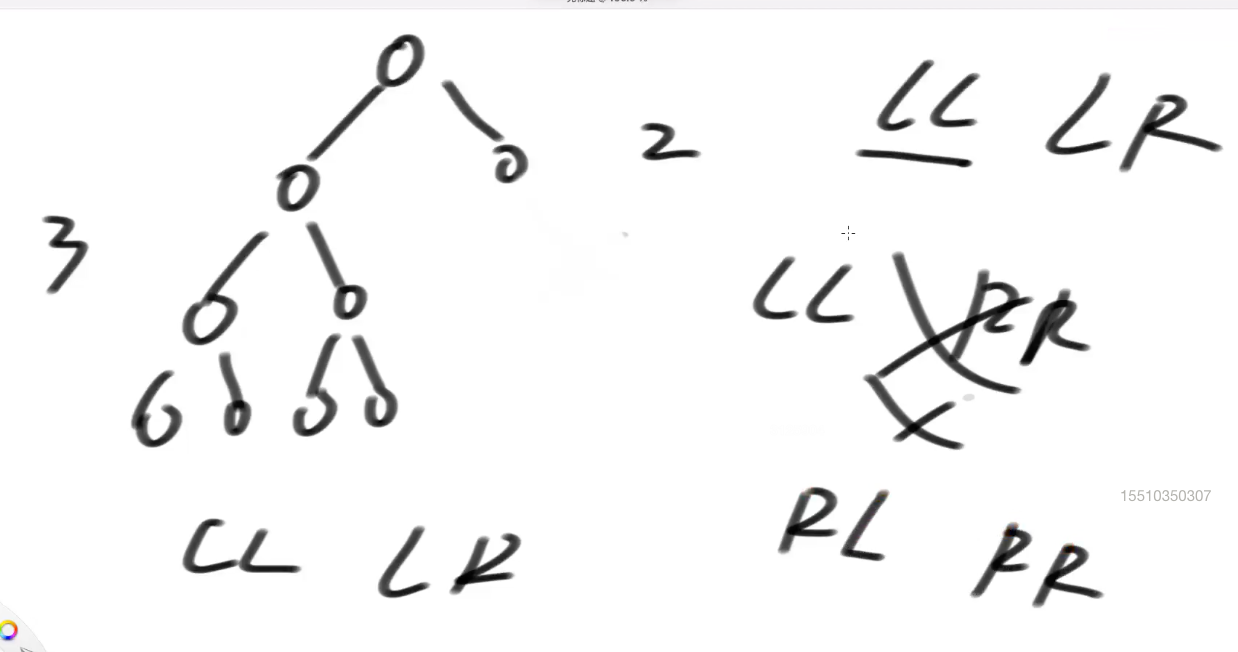
按照LL型调整后

 

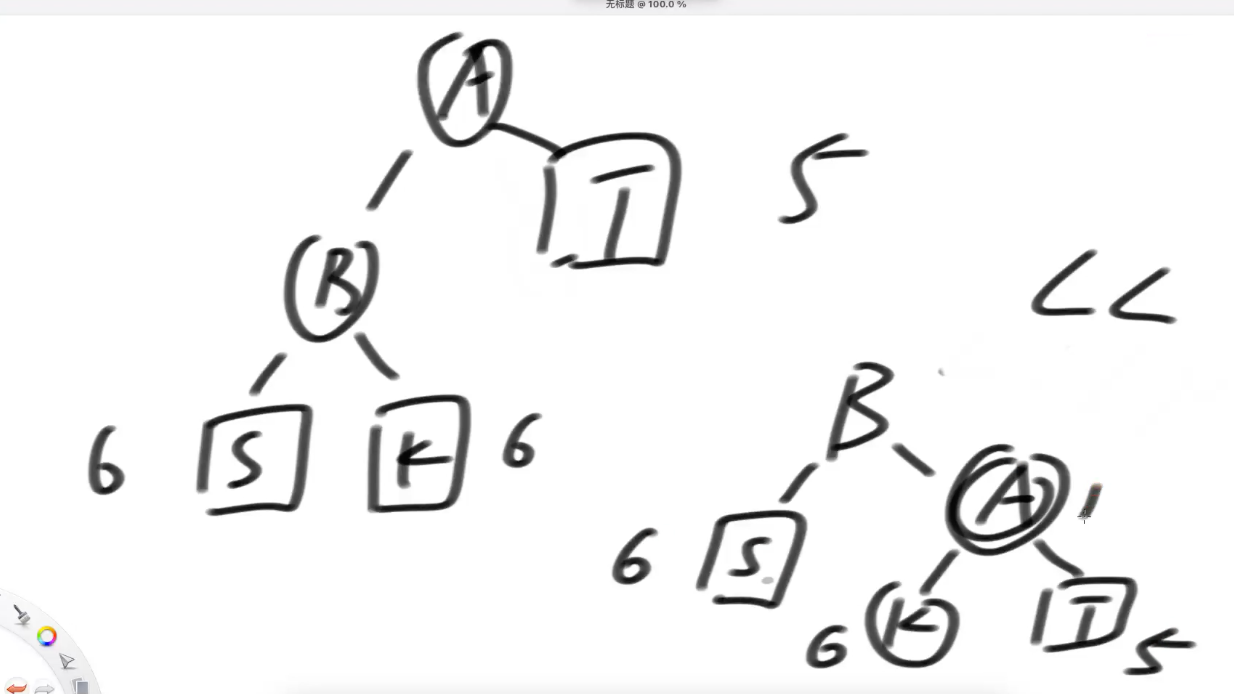
如果 按照LR型 调整时---》（可能会出现问题）

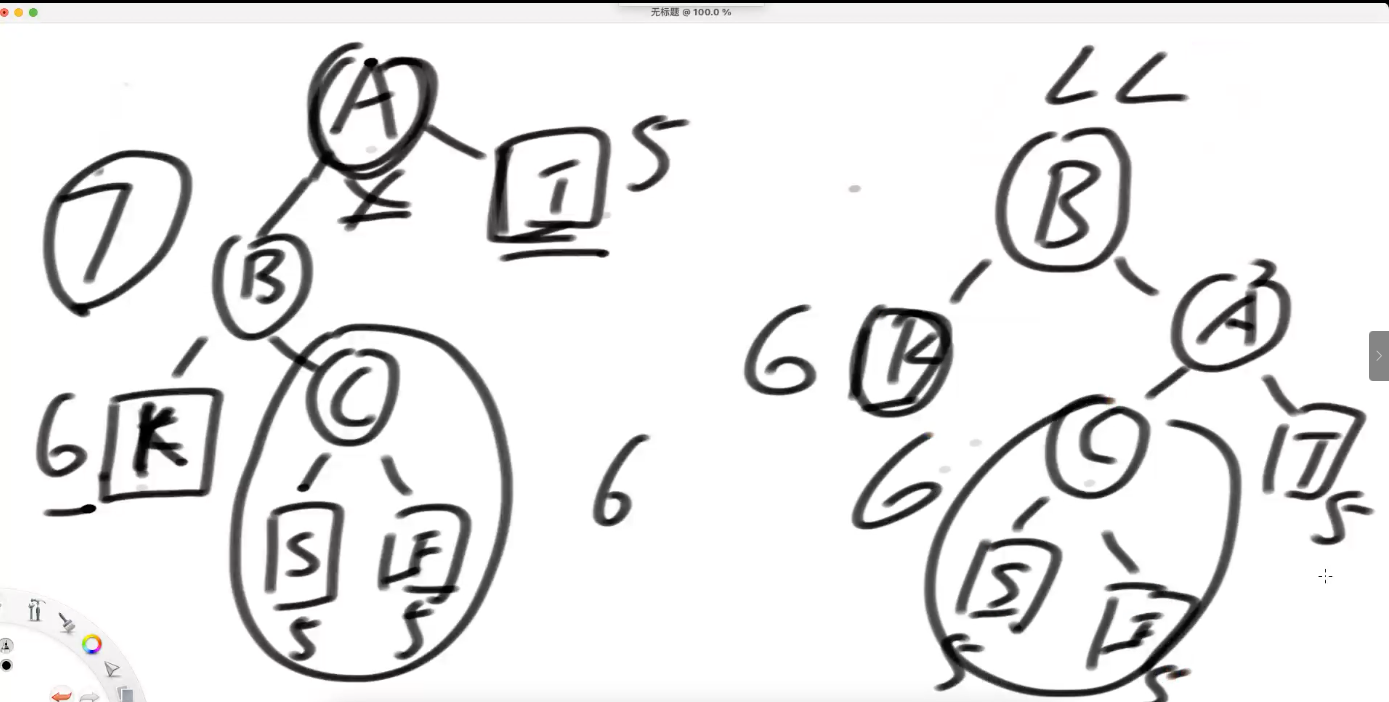按LL 是通的， 因为 C节点 的 左右子树 没有被拆分===》不会 引入 新的 不平衡问题

 

 

 但是 如果按照 LR调整下【里面 s的高度 为 5 】 ---》主要是因为重新 挂接 子树 到 新节点， 导致的 一次调整 不

 

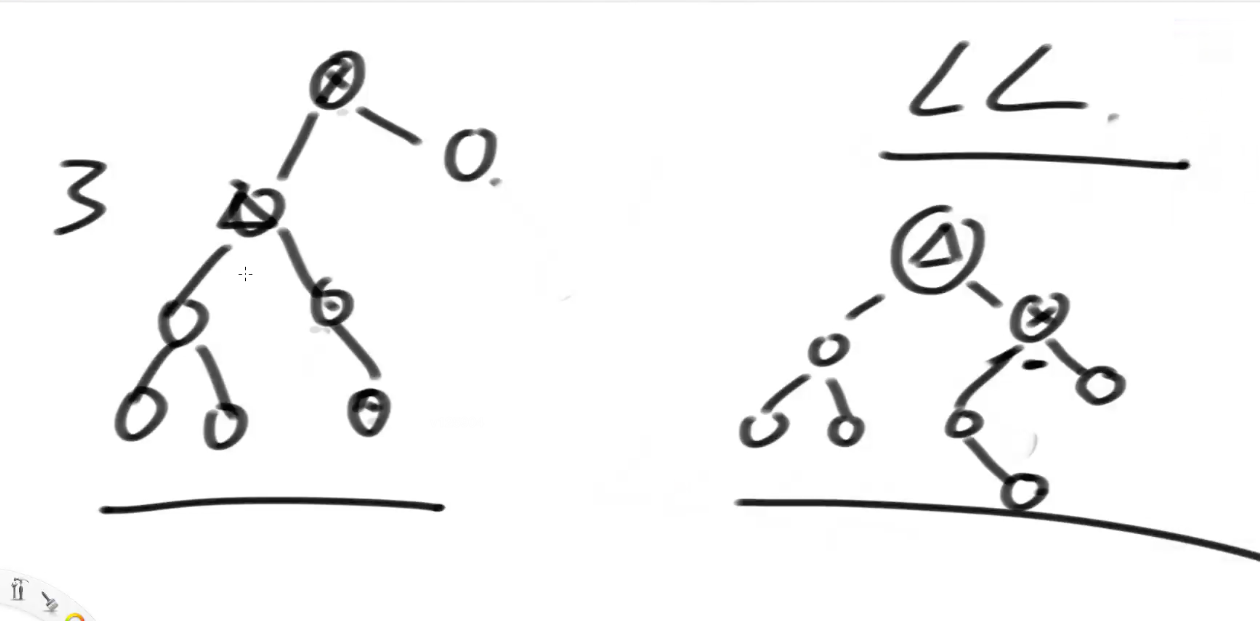
 重新举例：LL 和 LR型 同时存在 ===》按照 LL调整 重新举例  

 

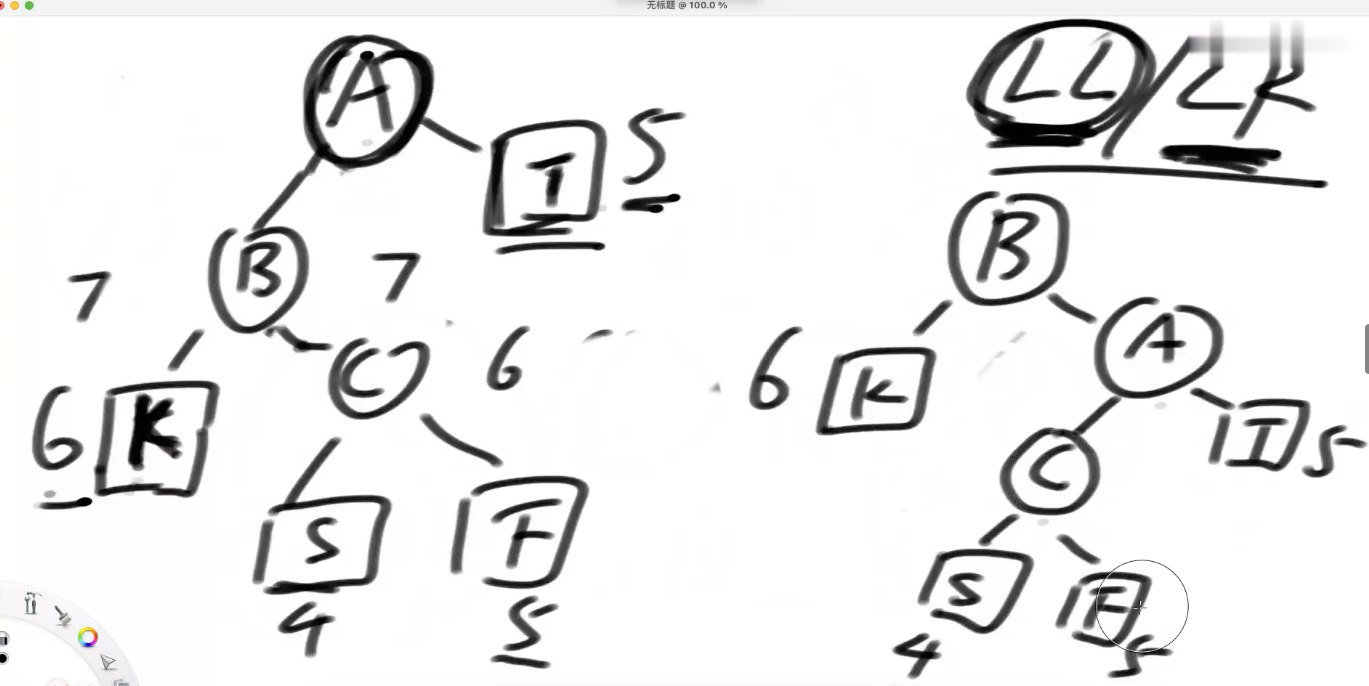
===》 按照 LR型 去调整 又出问题

 

 

 

 

 

 

 

 

 

 

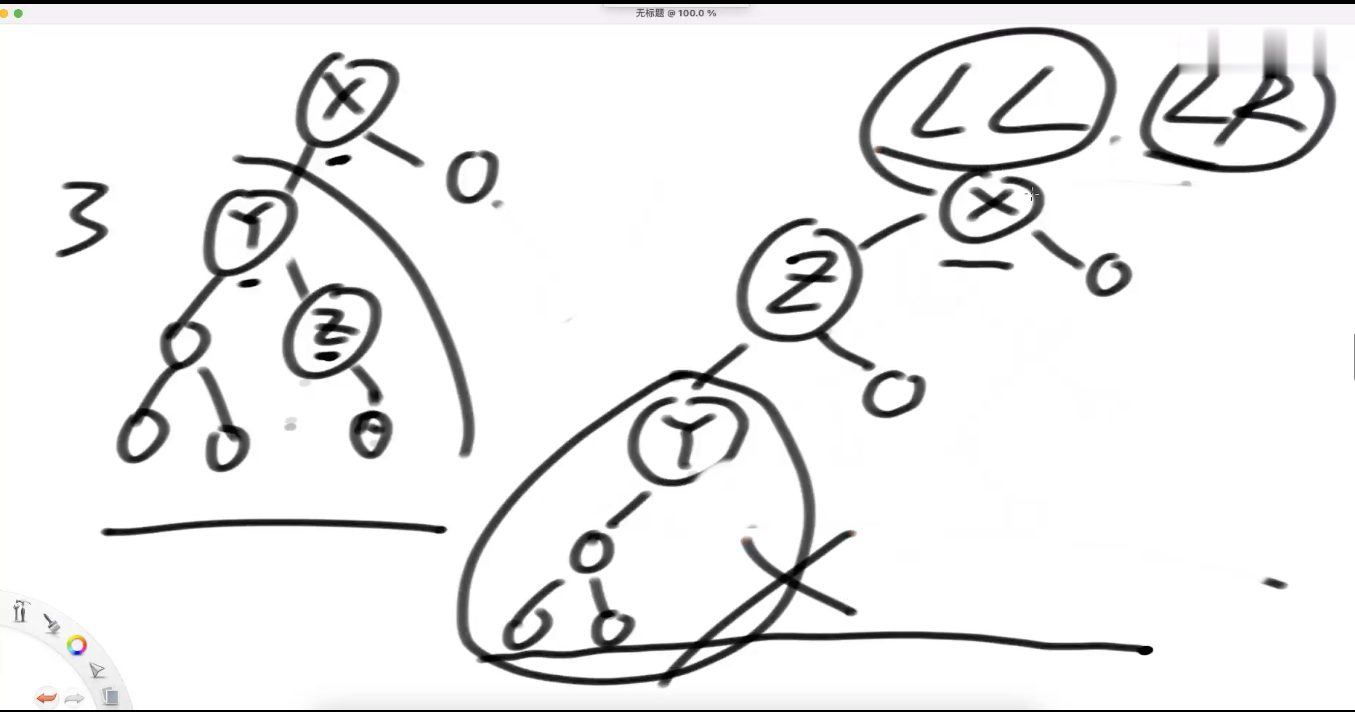
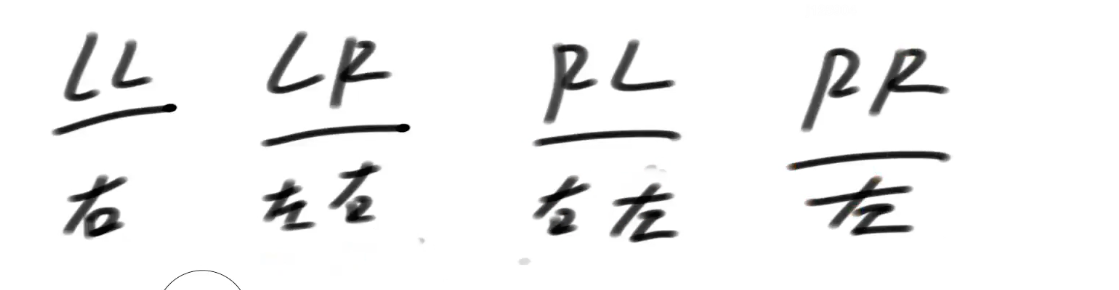
LL、LR共同成立 以LL为准;

 

RL,RR 共同成立 以RR为准

 

 【4】

顺便说了一下 数据库是如何基于有序表去建立索引的；

本来数据 在物理介质 上 是顺序存储；

但是 因为 遍历查找 太慢了；

可以 通过一些有 顺序的 字段 ，《可以比较大小》 ，通过这样 一种顺序 建立有序表

【5】搜索二叉树

 

【6】 avl 树 

|左树高度 - 右树高度| < 2

 

查找；

添加；===》每次添加完后， 平衡性 从当前根节点 每一个 都要重新调一遍

删除----》删除中间节点  【3】最难的情况【当前节点 左右 都有 孩子】：当前节点 的 右树 最 左节点 来代替；

 　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　 当前节点 的 左树 最 右节点 来代替；

【1】删除叶子节点 没有左右--》平衡性 上面每一个 节点都查

【2】删除节点 只有右孩子 ---》 用右孩子 代替当前节点

 

如何平衡： 左旋，右旋

 

四种类型 破坏 AVL的平衡性； 

 

【7】 右旋两段代码

private AVLNode<K, V> rightRotate( AVLNode<K, V> cur ) {
　　AVLNode<K, V> left = cur.l;
　　cur.l = left.r;
　　left.r = cur;
　　cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;
　　left.h = Math.max((left.l != null ? left.l.h : 0), (left.r != null ? left.r.h : 0)) + 1;
　　return left;
}

 

 

 

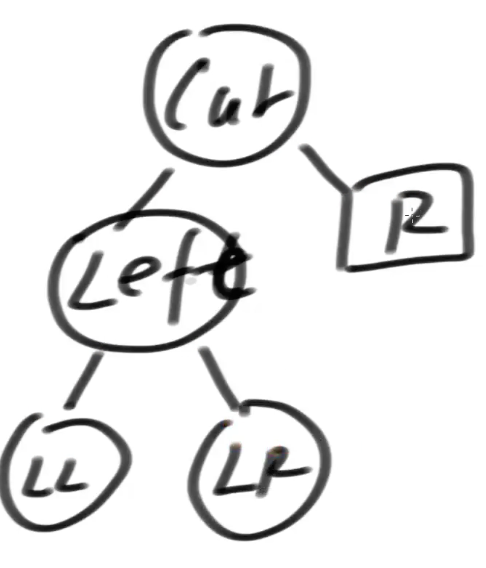
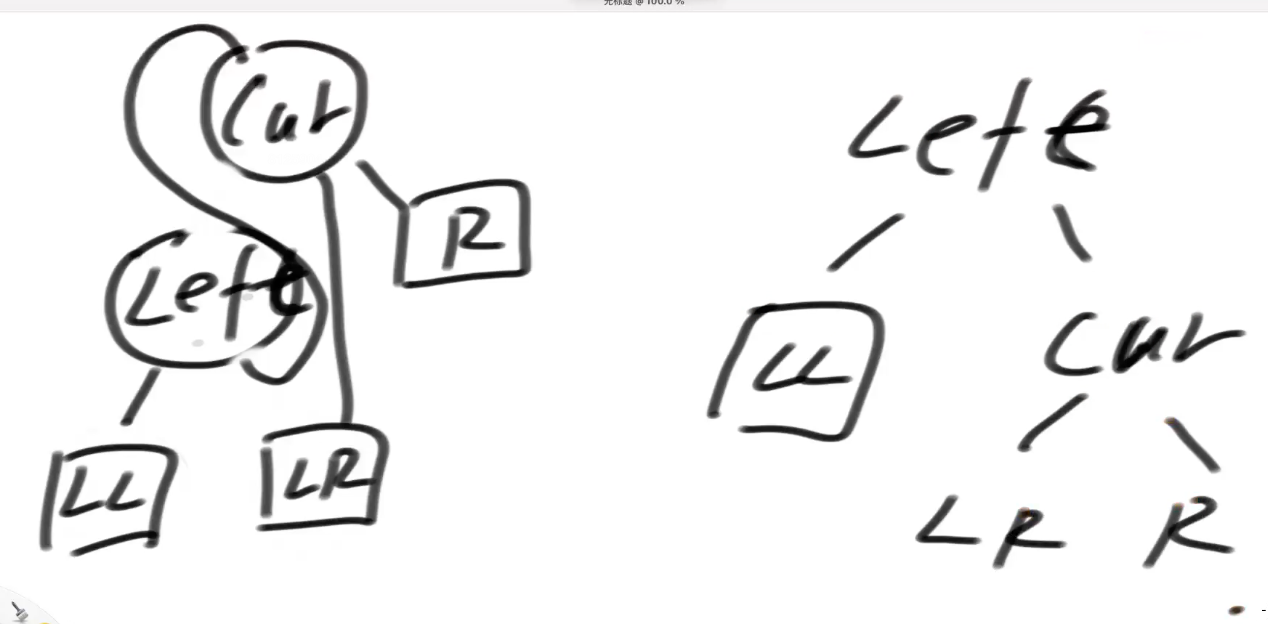
【8】 有序表 是个接口---》可以当成是一个技术标准，是个规范

AVL 树 本质就是 某颗 搜索二叉树 加上平衡性