2025.10.10 图论
最短路
P5304 [GXOI/GZOI2019] 旅行者
Hint：考虑从暴力优化. 图论建模，路径最短的两个关键点编号一定不同，按照二进制位划分成两个集合跑最短路.
最暴力的方法我们可以枚举关键点对跑最短路，时间复杂度 \(O(k^2m\log m)\).
显然有很多点对是没有任何意义的，考虑图论建模，一次跑多组最短路. 也就是直接将关键点分为两个集合，建立超级源点 \(S\) 连向其中一个集合的所有点，边权为 \(0\)；另一个集合所有点连向超级汇点，边权为 \(0\). 然后跑 \(S\rightarrow T\) 的最短路，当距离最近的两点被分到两个集合时，这样跑就能得到答案. 所以现在的问题就是如何划分关键点.
距离最近的两点编号一定不同，换言之至少有一个二进制位不同. 枚举二进制位，每次将当前二进制位不同的划分成两个集合，跑上面的最短路并更新答案即可. 时间复杂度 \(O(m\log m\log n)\).
P4366 [Code+#4] 最短路
Hint：直接连边边数可以达到 \(O(n^2)\)，但是点数是 \(O(n)\)，考虑拆位优化建图.
对每个点考虑贡献，发现如果一条新边有若干个二进制位有贡献，那么完全可以拆成若干位贡献再加起来. 也就是说类似于前缀优化建图，我们对于每一个 \(0\le u\le n\) 的点都向改变一位二进制位的点连边，就已经包含了所有可能的新边. 然后跑最短路即可.
P7515 [省选联考 2021 A 卷] 矩阵游戏
Hint：先推出一个不限制值域的答案，然后设出调整的变量，用差分约束求解.
令矩阵 \(A\) 最后一行和最后一列全为 \(0\)，可以解出一组符合 \(b_{i,j}\) 限制的解. 现在要尝试修改一个位置上的值，我们需要调整附近位置的值使得仍然满足限制.
进一步观察，发现我们可以对一行或一列进行 \(+x,-x,+x,-x\cdots\) 的操作而仍然满足限制. 设 \(r_i\) 为行上操作的值，\(c_i\) 为列上操作的值，可以列出操作矩阵：
但是这样的形式分讨稍显复杂，可以考虑对于所有 \(i\) 为偶数的 \(r_i\) 和 \(j\) 为奇数的 \(c_j\) 取相反数. 这仍然是满足限制的.
现在的形式非常优美了，考虑这个 \(x-y\) 的形式怎么用差分约束. 首先我们求得了一组解 \(a_{i,j}\)，所以 \(-a_{i,j}\le x-y\le 10^6-a_{i,j}\)，拆成两个不等式分别连边即可.
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define gc getwchar_unlocked
#define pc putwchar_unlocked
inline int rd(){
int x = 0, f = 1; char ch = gc();
while(ch < '0' || ch > '9'){ if(ch == '-') f = -1; ch = gc(); }
while(ch >= '0' && ch <= '9'){ x = x * 10 + (ch ^ 48); ch = gc(); }
return x * f;
}
inline void wt(int x) {
static int stk[40],tp=0;
if(x<0) pc('-'),x=-x;
do{
stk[++tp]=x%10;x/=10;
}while(x);
while(tp) pc((char)(stk[tp--]+'0'));
}
const int maxn = 3e2 + 10, maxnm = 9e4 + 10; const ll inff = 0x3f3f3f3f3f3f3f3f;
int T, n, m, a[maxn][maxn], b[maxn][maxn];
int s = 1;
vector<array<int, 2> > e[maxn << 1];
ll dis[maxn << 1]; bool inq[maxn << 1]; int cnt[maxn << 1];
bool spfa() {
for(int i = 1; i <= n + m; i++) inq[i] = cnt[i] = 0, dis[i] = inff;
deque<int> q; q.push_back(s), inq[s] = true, dis[s] = 0, cnt[s] = 1;
while(q.size()) {
int u = q.front(); q.pop_front(), inq[u] = false;
++cnt[u]; if(cnt[u] > n + m) return false;
for(auto [v, w] : e[u]) {
if(dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
if(!inq[v]) {
if(q.size() && dis[v] < dis[q[0]]) q.push_front(v);
else q.push_back(v);
inq[v] = true;
}
}
}
} return true;
}
void solve() {
for(int i = 1; i <= n + m; i++) vector<array<int, 2> >().swap(e[i]);
for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) a[i][j] = 0;
n = rd(), m = rd();
for(int i = 1; i < n; i++) for(int j = 1; j < m; j++) b[i][j] = rd();
for(int i = n - 1; i >= 1; i--) for(int j = m - 1; j >= 1; j--) {
a[i][j] = b[i][j] - a[i + 1][j] - a[i][j + 1] - a[i + 1][j + 1];
}
for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) {
int mx = 1e6 - a[i][j], mi = -a[i][j];
if((i + j) & 1) e[j + n].push_back({i, -mi}), e[i].push_back({j + n, mx});
else e[j + n].push_back({i, mx}), e[i].push_back({j + n, -mi});
}
if(spfa()) {
puts("YES");
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
if ((i + j) & 1) a[i][j] -= dis[i];
else a[i][j] += dis[i];
if ((i + j) & 1) a[i][j] += dis[j + n];
else a[i][j] -= dis[j + n];
wt(a[i][j]); pc(' ');
} puts("");
}
}
else puts("NO");
return;
}
int main() {
// ios :: sync_with_stdio(false); cin.tie(0); cout.tie(0);
// freopen("P7515_13.in", "r", stdin);
// freopen("myout.out", "w", stdout);
T = rd(); while(T--) solve();
return 0;
}
为啥把链式前向星改成 vector 快了 \(25\) 倍？
连通性
P4630 [APIO2018] 铁人两项
有经典结论：对于点双内任意三点 \(x,y,z\)，一定存在 \(x\rightarrow y,y\rightarrow z\) 的路径只在 \(y\) 相交. 考虑反证法，若不存在只在 \(y\) 相交的两路径路径，那么两路径至少还存在另一个交点 \(u\). 发现 \(u\) 必然是割点，否则若存在另外一组也至少存在另一个交点 \(v\) 的路径，就可以构造出只在 \(y\) 相交的路径. 如图：
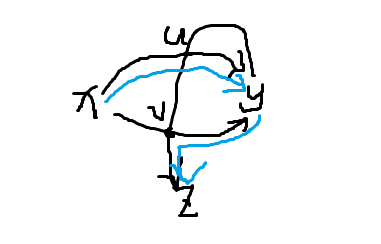
这与 \(x,y,z\) 在点双内相悖，故原结论成立.
构造
CF1325F Ehab's Last Theorem
比较厉害的构造题.
考虑
浙公网安备 33010602011771号