#2.笛卡尔树

“不会线性可以用线段树睡过去”

笛卡尔树

0x01. 什么是笛卡尔树

定义(摘自OI wiki)

笛卡尔树是一种二叉树，每一个节点由一个键值二元组 \((k,w)\) 构成。要求 \(k\) 满足二叉搜索树的性质，而 \(w\) 满足堆的性质。如果笛卡尔树的 \(k,w\) 键值确定，且 \(k\) 互不相同，\(w\) 也互不相同，那么这棵笛卡尔树的结构是唯一的。

浅显地说：

一个小根堆（或大根堆），满足二叉搜索树的性质，其中序遍历为原序列。

0x02. 为什么要使用笛卡尔树

性质（以小根堆为例）：

1. 二叉树上存储形如（\(u_i, w_i\)）的点对，\(u_i\) 满足二叉搜索树的性质，\(w_i\) 满足小根堆的性质。（详见下文的解释）
2. 以 \(u\) 为根的子树是一段连续的区间, 且 \(u\) 是这段区间的最小值。
3. 任意区间 \([l, r]_{min} = LCA(l, r)\)

建树复杂度：

• \(u_i\) 无序：考虑线段树维护区间最小值，查询 \(O(log_n)\), \(n\) 个数总计 \(O(nlog_n)\)
• \(u_i\) 有序：考虑单调栈维护单增序列，复杂度 \(O(n)\)

0x03. 具体实现与代码

P5854 【模板】笛卡尔树

题意：给定一个 \(1\sim n\) 的排列 \(p\) ，构建其笛卡尔树。设 \(l_i,r_i\) 分别表示节点 \(i\) 的左右儿子的编号，输出一行，分别表示 \(Xor_{i=1}^n i×(l_i +1)\) 和 \(Xor_{i=1}^n i×(r_i +1)\)

线段树实现笛卡尔树：

哎呀就是线段树板子
注意：此题数据范围 \(n \le1e7\) 无法通过

---

单调栈实现笛卡尔树：

将笛卡尔树的右链用单调栈维护，每次在单调栈中找到当前 \(w_i\) 值对应的前一个位置，让 \(w_i\) 作为它的右儿子以维护单调栈的单调性；由于上一个弹出的值一定是比 \(w_i\) 大的值中的最小值，所以直接将其作为当前节点的左儿子以维护小根堆的性质。

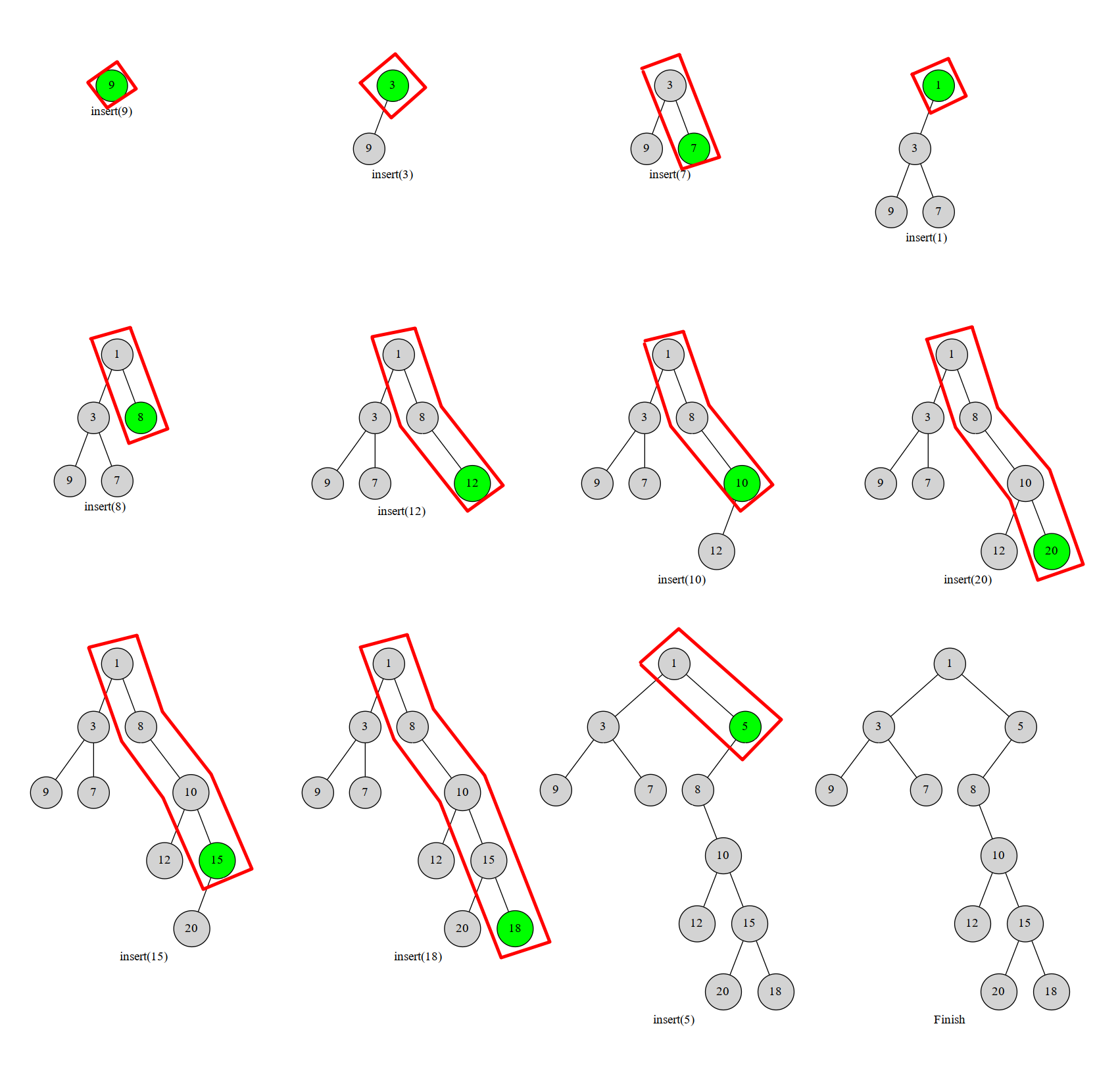
注：图片来自OI wiki

注意：原题 \(\oplus i*(lc[i]+1)\)会炸 int ,记得开long long

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

inline int read() {
	int f = 1, otto = 0;
	char a = getchar();
	while(!isdigit(a)) {
		if(a == '-') f = -1;
		a = getchar();
	}
	while(isdigit(a)) {
		otto = (otto << 1) + (otto << 3) + (a ^ 48);
		a = getchar();
	}
	return f * otto;
}

const int maxn = 1e7 + 10;
int lc[maxn], rc[maxn], a[maxn], stk[maxn];

int main() {
	int n = read();
	for(int i = 1; i <= n; i++) a[i] = read();
	
	int top = 0;
	for(int i = 1; i <= n; i++) {
		int k = top;
		while(k && a[i] < a[stk[k]]) k--;
		if(k) rc[stk[k]] = i;
		if(k < top) lc[i] = stk[k + 1];
		stk[++k] = i;
		top = k;
	}
	
	ll ans1 = 0, ans2 = 0;
	for(ll i = 1; i <= n; i++) {
		ans1 ^= (i * (lc[i] + 1));
		ans2 ^= (i * (rc[i] + 1));
	}
	printf("%lld %lld", ans1, ans2);
}