数据结构---堆

堆

在学数据结构堆之前，我以为我将要学习的是堆栈中的“堆”，可以与动态分配内存有关的堆的数据结构学个清楚了，开始学习时我才发现，此堆非彼堆，这个数据结构中的堆，与我心想的堆并非是同一类玩意。

堆的原理:

堆是利用完全二叉树的结构来处理一组数据，其特点如下
1> 每个节点最多可以有两个节点。
2> 根节点的键值是所有堆节点中键值最大或最小，每个父节点都比其孩子节点的键值要大或者小。（大或小取决于这是一个最大堆，还是最小堆）
3> 除了根节点可以没有兄弟节点，最后一个左子节点可以没有兄弟节点，其他所有的节点必须要有兄弟节点。

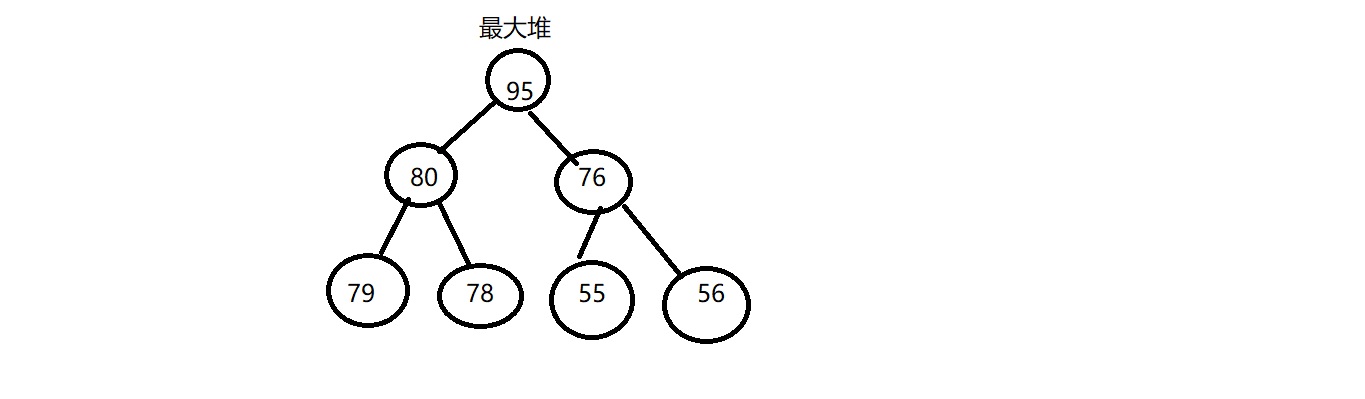
来看看上面这个最大堆吧，
如果，去掉键值为56的节点，其还是一个最大堆，但如果去掉的是55这个节点，就不再是一个最大堆了，这也就是特点3的情况。

最大堆的代码实现

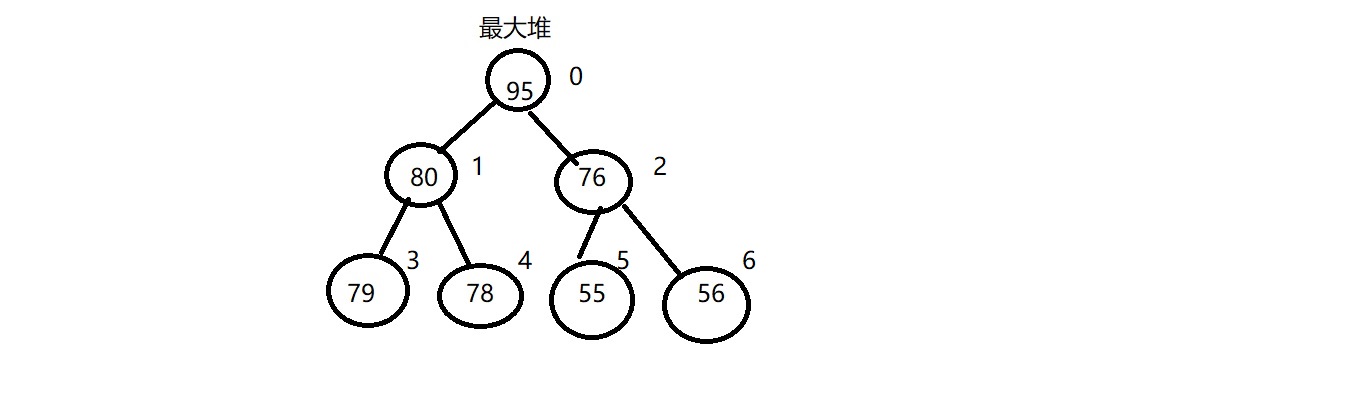
这里我选择用数组来表示这个堆，因为通过观察我们不难发现堆中的节点的下标与其子节点的下标的关系。
例如：父节点i的左子节点为2i+1，右子节点为2i+2

### 最大堆的结构体定义
typedef struct _Heap {
	int* arr;
	size_t size;
	size_t capacity;
}Heap;

最大堆的建立与初始化

void initHeap(Heap& heap, int* resourse, int size);
//static仅供内部使用函数
static void buildHeap(Heap& heap);
//将一个序号为index的节点向下调整，用在建堆的过程中
static void adjustDown(Heap& heap, unsigned index);
//将一个序号为index的节点向上调整，用在堆插入元素的过程中
static void adjustUp(Heap& heap, unsigned index);

void initHeap(Heap& heap, int* resourse, int size) {
	if (!resourse || size <= 0)  return;
	int capacity = DEFAULT_CAPACITY > size ? DEFAULT_CAPACITY : size;
	heap.size = size;
	heap.capacity = capacity;
	heap.arr = new int[capacity];
	if (!heap.arr) return;
	memcpy(heap.arr, resourse, size * sizeof(int));
	buildHeap(heap);
	return;
}
//建最大堆，从最后一个父节点开始，for循环持续到根节点结束
void buildHeap(Heap& heap) {
	int i = 0;
	for (i = heap.size / 2 - 1;i >= 0;i--) {
		adjustDown(heap, i);
	}
}
//将下标为index的节点向下调整，直到节点大于两个子节点，或者是节点沉入到最后一层for循环结束
void adjustDown(Heap& heap, unsigned index) {
	unsigned parent, child;
	int cur = 0;
	for (parent = index;parent * 2 + 1 < heap.size;parent = child) {
		cur = heap.arr[parent];
		child = parent * 2 + 1;//先将child指向父节点的左子节点
		if ((child + 1 < heap.size) && (heap.arr[child + 1] > heap.arr[child])) { //(child + 1 < heap.size)为了避免最后一个左子节点没有兄弟节点的尴尬情况，防止越界

			child++;//如果右子节点的值大于左子节点的值，则child指向右子节点
		}
		if (heap.arr[parent] >= heap.arr[child]) {//如果父节点大于最大的子节点，则调整完毕，退出循环
			break;
		}
		else {//否则，父节点下移，继续调整。
			heap.arr[parent] = heap.arr[child];
			heap.arr[child] = cur;
		}
	}
}

void adjustUp(Heap& heap, unsigned index) {
	if (index < 0 || index >= heap.size) return;
	int parent, cur;
	while (index > 0) {
		parent = (index - 1) / 2;
		cur = heap.arr[parent];
		if (heap.arr[parent] < heap.arr[index]) {//待调整的节点的值大于父节点，则待调整节点与父节点交换位置
			heap.arr[parent] = heap.arr[index];
			heap.arr[index] = cur;
		}
		else {//否则，则没有向上调整的必要，调整完毕，退出循环
			break;
		}
		index = parent;
	}
	return;
}

附上一张关于建堆的过程的图，方便理解：

堆中插入元素与删除元素

void insertHeap(Heap& heap, int value) {
	if (heap.size == heap.capacity) {//堆已满
		cout << "堆已满,无法再插入数据!" << endl;
		return;
	}
	heap.arr[heap.size] = value;
	heap.size++;
	adjustUp(heap, heap.size - 1);
	return;
}
void popHeap(Heap& heap, int& value){
	if (heap.size == 0) {
		cout << "duiyikong" << endl;
		return;
	}
	value = heap.arr[0];
	heap.arr[0] = heap.arr[heap.size - 1];
	heap.arr[heap.size - 1] = 0;
	heap.size--;
	adjustDown(heap, 0);
	return;
}

堆遍历及销毁

void printHeap(Heap& heap) {
	if (!heap.arr || heap.size <= 0) { 
		cout << "some problems" << endl;
		return; 
	}
	cout << "开始遍历堆" << endl;
	for (unsigned i = 0;i < heap.size;i++) {
		cout << heap.arr[i] << endl;
	}
	return;
}
void destroyHeap(Heap& heap)
{
	if (heap.arr) {
		delete[] heap.arr;
		return;
	}
	return;
}

堆排序

//将堆初始化为堆排序用的堆,heap的size的值就等于size。
void initHeapSort(Heap& heap, int* resourse, int size){
	if (!resourse || size <= 0)  return;
	heap.size = size;
	heap.capacity = size;
	heap.arr = resourse;
	buildHeap(heap);
	return;
}
//堆排序
/***********************************************************
算法思路:先将最大的根节点与最后一个根节点交换位置，此时我们得到的是
最大的值，然后heap.size-1，在重复上一步操作，由于size-1了，第二遍操作，
我们得到的是第二大的元素放在最后第二个节点。如是循环，直到heap.size=0,
堆排序已经完成，此时堆中的数组为升序排列。
*************************************************************/
void heapSort(Heap& heap){
	int tmp;
	while (heap.size > 0) {
		tmp = heap.arr[0];
		heap.arr[0] = heap.arr[heap.size - 1];
		heap.arr[heap.size - 1] = tmp;
		heap.size--;
		adjustDown(heap, 0);
	}
}
//堆排序测试函数
void testHeapSort() {
	Heap heap;
	int a[] = { 12,43,54,12,32,43,6,2,1,43 };
	initHeapSort(heap, a, sizeof(a) / sizeof(int));
	heapSort(heap);
	cout << "heap.size = " << heap.size << endl;
	cout << "After sorting" << endl;
	for (int i = 0;i < sizeof(a) / sizeof(int);i++) {
		cout << a[i] << "\t" << endl;
	}
}