一致性哈希与并行算法
一致性哈希
分布式存储结构最常见的结构
1.哈希域变成环的设计
2.虚拟节点技术
场景描述
假设,我们有三台缓存服务器,用于缓存图片,我们为这三台缓存服务器编号为0号、1号、2号,现在,有3万张图片需要缓存,我们希望这些图片被均匀的缓存到这3台服务器上,以便它们能够分摊缓存的压力。也就是说,我们希望每台服务器能够缓存1万张左右的图片,那么,我们应该怎样做呢?如果我们没有任何规律的将3万张图片平均的缓存在3台服务器上,可以满足我们的要求吗?可以!但是如果这样做,当我们需要访问某个缓存项时,则需要遍历3台缓存服务器,从3万个缓存项中找到我们需要访问的缓存,遍历的过程效率太低,时间太长,当我们找到需要访问的缓存项时,时长可能是不能被接受的,也就失去了缓存的意义,缓存的目的就是提高速度,改善用户体验,减轻后端服务器压力,如果每次访问一个缓存项都需要遍历所有缓存服务器的所有缓存项,想想就觉得很累,那么,我们该怎么办呢?原始的做法是对缓存项的键进行哈希,将hash后的结果对缓存服务器的数量进行取模操作,通过取模后的结果,决定缓存项将会缓存在哪一台服务器上,这样说可能不太容易理解,我们举例说明,仍然以刚才描述的场景为例,假设我们使用图片名称作为访问图片的key,假设图片名称是不重复的,那么,我们可以使用如下公式,计算出图片应该存放在哪台服务器上。
hash(图片名称)% N
因为图片的名称是不重复的,所以,当我们对同一个图片名称做相同的哈希计算时,得出的结果应该是不变的,如果我们有3台服务器,使用哈希后的结果对3求余,那么余数一定是0、1或者2,没错,正好与我们之前的服务器编号相同,如果求余的结果为0, 我们就把当前图片名称对应的图片缓存在0号服务器上,如果余数为1,就把当前图片名对应的图片缓存在1号服务器上,如果余数为2,同理,那么,当我们访问任意一个图片的时候,只要再次对图片名称进行上述运算,即可得出对应的图片应该存放在哪一台缓存服务器上,我们只要在这一台服务器上查找图片即可,如果图片在对应的服务器上不存在,则证明对应的图片没有被缓存,也不用再去遍历其他缓存服务器了,通过这样的方法,即可将3万张图片随机的分布到3台缓存服务器上了,而且下次访问某张图片时,直接能够判断出该图片应该存在于哪台缓存服务器上,这样就能满足我们的需求了,我们暂时称上述算法为HASH算法或者取模算法,取模算法的过程可以用下图表示。
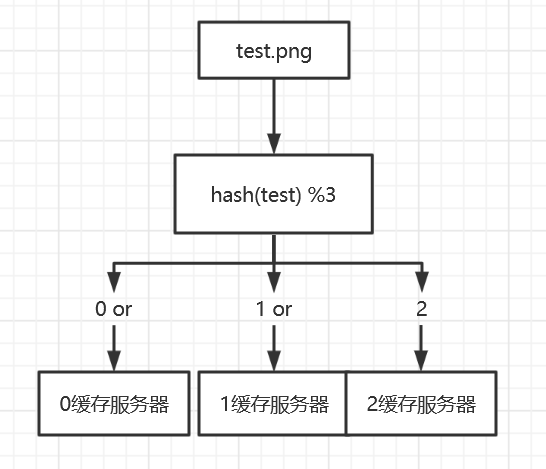
上述算法会出现的问题。
问题1:当缓存服务器数量发生变化时,会引起缓存的雪崩,可能会引起整体系统压力过大而崩溃(大量缓存同一时间失效)。
问题2:当缓存服务器数量发生变化时,几乎所有缓存的位置都会发生改变,怎样才能尽量减少受影响的缓存呢?
----------------------------------------> 一致性哈希既可以做到迁移代价很低,也可以做到负载均衡
哈希域变成环的设计
原来的数据决定归属:key-->hash值--->hashcode % 3 --->数据归属
假设选取的hash函数是MD5,返回值是0~2^64-1的空间,把空间想象成一个环,就像钟表一样,钟表的圆可以理解成由60个点组成的圆,而此处我们把这个圆想象成由2^64个点组成的圆,示意图如下:
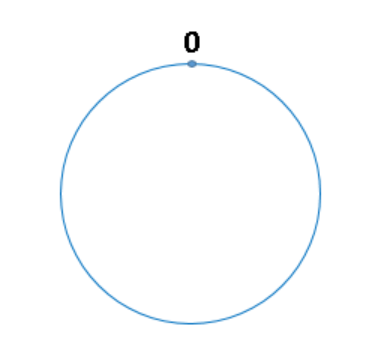
圆环的正上方的点代表0,0点右侧的第一个点代表1,以此类推,2、3、4、5、6……直到2^64-1,也就是说0点左侧的第一个点代表2^64-1我们把这个由2的32次方个点组成的圆环称为hash环。
假设我们有3台缓存服务器,服务器A、服务器B、服务器C,那么,在生产环境中,这三台服务器肯定有自己的IP地址,我们使用它们各自的IP地址进行哈希计算,使用哈希后的结果对2^64取模,可以使用如下公式示意。
hash(服务器A的IP地址) % 2^64
通过上述公式算出的结果一定是一个0到2^64-1之间的一个整数,我们就用算出的这个整数,代表服务器A,既然这个整数肯定处于0到2^64-1之间,那么,上图中的hash环上必定有一个点与这个整数对应,而我们刚才已经说明,使用这个整数代表服务器A,那么,服务器A就可以映射到这个环上,同理,服务器B与服务器C也可以通过相同的方法映射到上图中的hash环中
hash(服务器B的IP地址) % 2^64
hash(服务器C的IP地址) % 2^64
通过上述方法,可以将服务器B与服务器C映射到上图中的hash环上,示意图如下
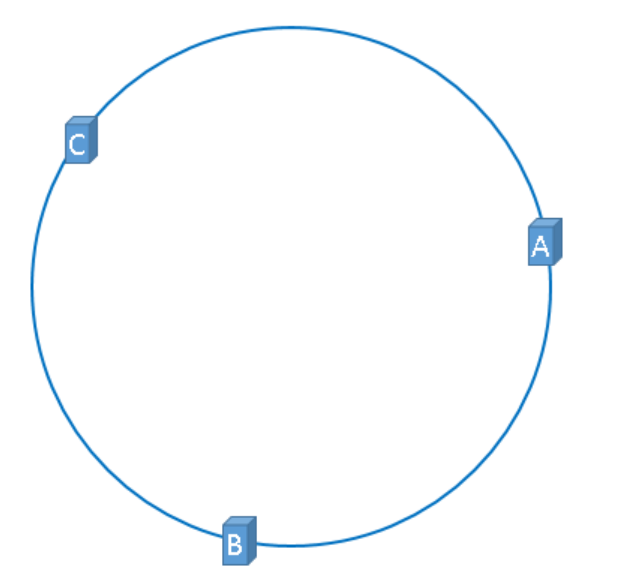
到目前为止,我们已经把缓存服务器与hash环联系在了一起,我们通过上述方法,把缓存服务器映射到了hash环上,那么使用同样的方法,我们也可以将需要缓存的对象映射到hash环上。
我们需要使用缓存服务器缓存图片,而且我们仍然使用图片的名称作为找到图片的key,那么我们使用如下公式可以将图片映射到上图中的hash环上。
hash(图片名称) % 2^64
映射后的示意图如下,下图中的橘黄色圆形表示图片
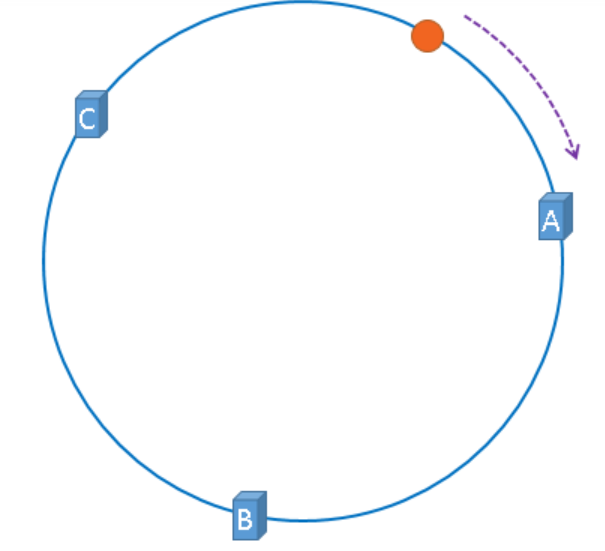
现在服务器与图片都被映射到了hash环上,那么上图中的这个图片到底应该被缓存到哪一台服务器上呢?上图中的图片将会被缓存到服务器A上,为什么呢?因为从图片的位置开始,沿顺时针方向遇到的第一个服务器就是A服务器,所以,上图中的图片将会被缓存到服务器A上,如下图所示。
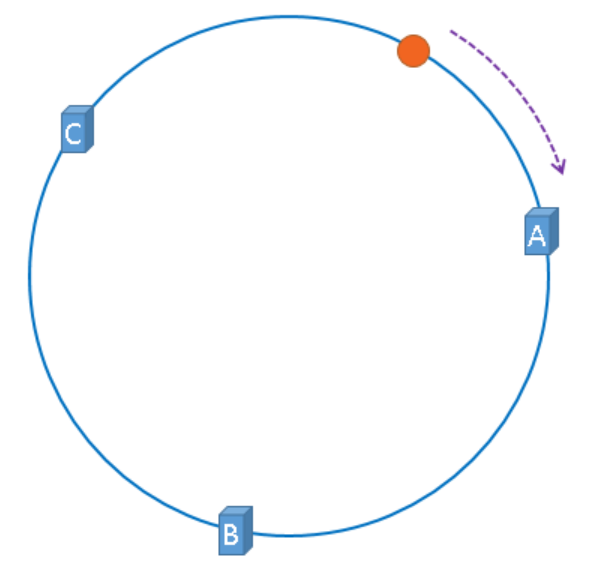
一致性哈希算法就是通过这种方法,判断一个对象应该被缓存到哪台服务器上的,将缓存服务器与被缓存对象都映射到hash环上以后,从被缓存对象的位置出发,沿顺时针方向遇到的第一个服务器,就是当前对象将要缓存于的服务器,由于被缓存对象与服务器hash后的值是固定的,所以,在服务器不变的情况下,一张图片必定会被缓存到固定的服务器上,那么,当下次想要访问这张图片时,只要再次使用相同的算法进行计算,即可算出这个图片被缓存在哪个服务器上,直接去对应的服务器查找对应的图片即可。
如何顺时针的找到应该被缓存到哪台服务器上?假设服务器有几十万台,难道每次都需要遍历吗?
-------->我们可以将每个机器的哈希值算出来后进行从小到大排序,然后每个数据在排序中的数组中进行二分查找比自己大的那个数在哪儿。
一致性哈希算法的优点
如果简单的对服务器数量进行取模,那么当服务器数量发生变化时,会产生缓存的雪崩,从而很有可能导致系统崩溃,那么使用一致性哈希算法,能够避免这个问题吗?我们来模拟一遍,即可得到答案。
假设,服务器B出现了故障,我们现在需要将服务器B移除,那么,我们将上图中的服务器B从hash环上移除即可,移除服务器B以后示意图如下。
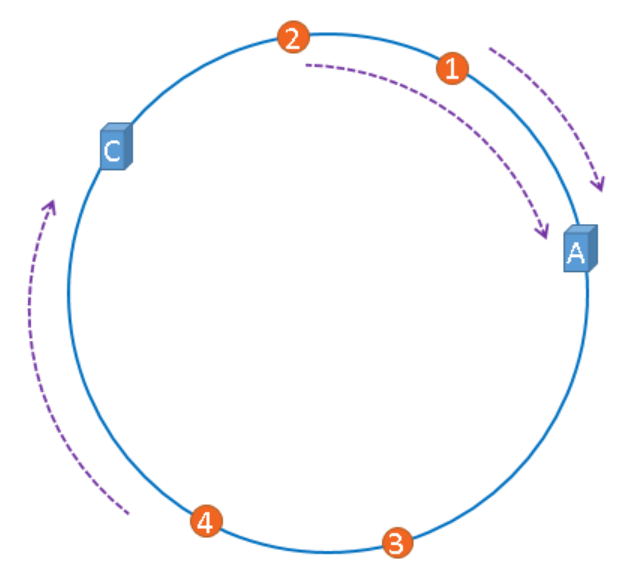
在服务器B未移除时,图片3应该被缓存到服务器B中,可是当服务器B移除以后,按照之前描述的一致性哈希算法的规则,图片3应该被缓存到服务器C中,因为从图片3的位置出发,沿顺时针方向遇到的第一个缓存服务器节点就是服务器C,也就是说,如果服务器B出现故障被移除时,图片3的缓存位置会发生改变。
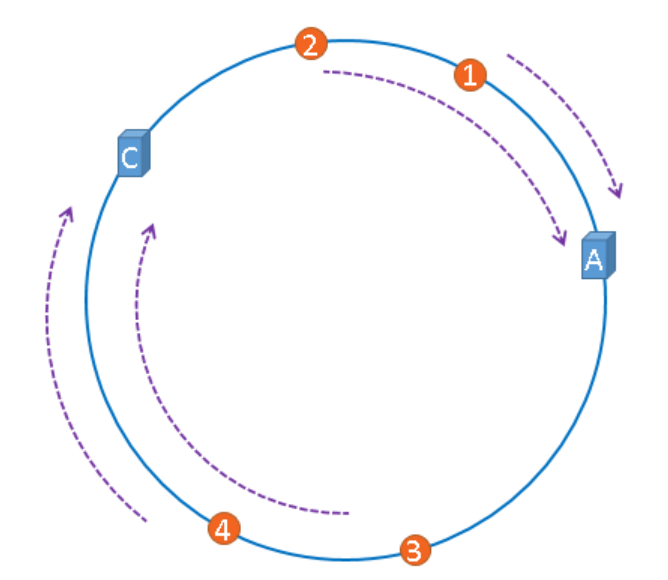
图片4仍然会被缓存到服务器C中,图片1与图片2仍然会被缓存到服务器A中,这与服务器B移除之前并没有任何区别,这就是一致性哈希算法的优点,如果使用之前的hash算法,服务器数量发生改变时,所有服务器的所有缓存在同一时间失效了,而使用一致性哈希算法时,服务器的数量如果发生改变,并不是所有缓存都会失效,而是只有部分缓存会失效,前端的缓存仍然能分担整个系统的压力,而不至于所有压力都在同一时间集中到后端服务器上。
hash环的偏斜
在实际的映射中,服务器可能会被映射成如下模样。
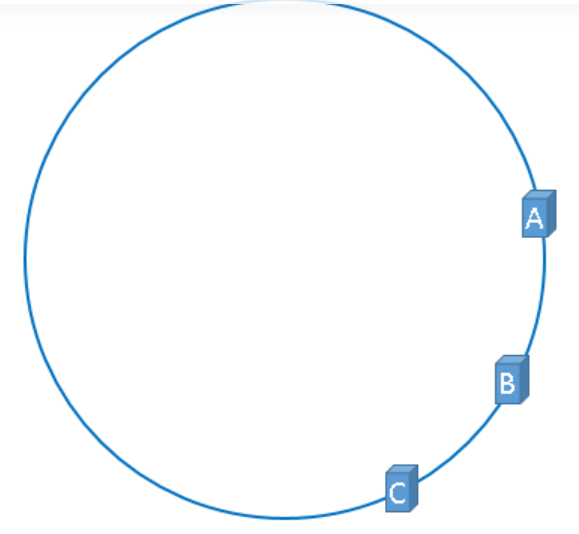
如果服务器被映射成上图中的模样,那么被缓存的对象很有可能大部分集中缓存在某一台服务器上,如下图所示。
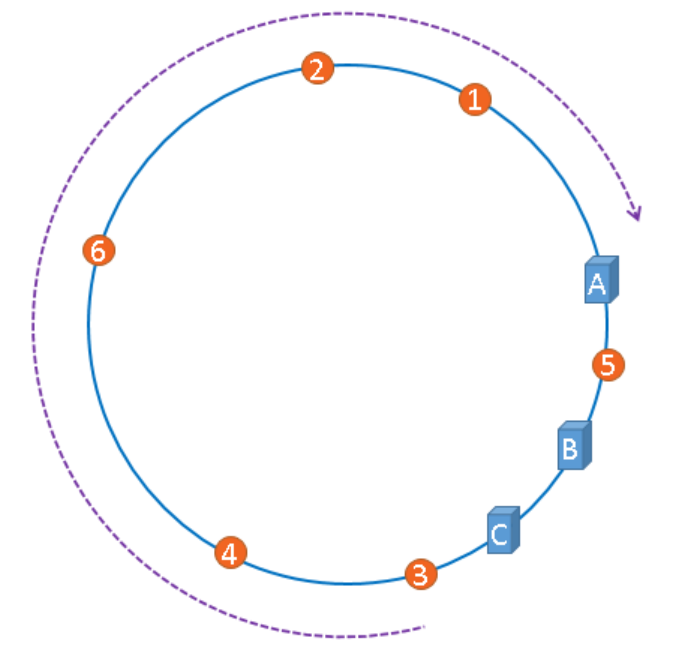
上图中,1号、2号、3号、4号、6号图片均被缓存在了服务器A上,只有5号图片被缓存在了服务器B上,服务器C上甚至没有缓存任何图片,如果出现上图中的情况,A、B、C三台服务器并没有被合理的平均的充分利用,缓存分布的极度不均匀,而且,如果此时服务器A出现故障,那么失效缓存的数量也将达到最大值,在极端情况下,仍然有可能引起系统的崩溃,上图中的情况则被称之为hash环的偏斜,那么,我们应该怎样防止hash环的偏斜呢?一致性hash算法中使用”虚拟节点”解决了这个问题。
虚拟节点技术
由于我们只有3台服务器,当我们把服务器映射到hash环上的时候,很有可能出现hash环偏斜的情况,因为离散数学很可能让俩个服务器挨着很近,当hash环偏斜以后,缓存往往会极度不均衡的分布在各服务器上,如果想要均衡的将缓存分布到3台服务器上,最好能让这3台服务器尽量多的、均匀的出现在hash环上,但是,真实的服务器资源只有3台,我们怎样凭空的让它们多起来呢,没错,就是凭空的让服务器节点多起来,既然没有多余的真正的物理服务器节点,我们就只能将现有的物理节点通过虚拟的方法复制出来,这些由实际节点虚拟复制而来的节点被称为”虚拟节点”。加入虚拟节点以后的hash环如下。
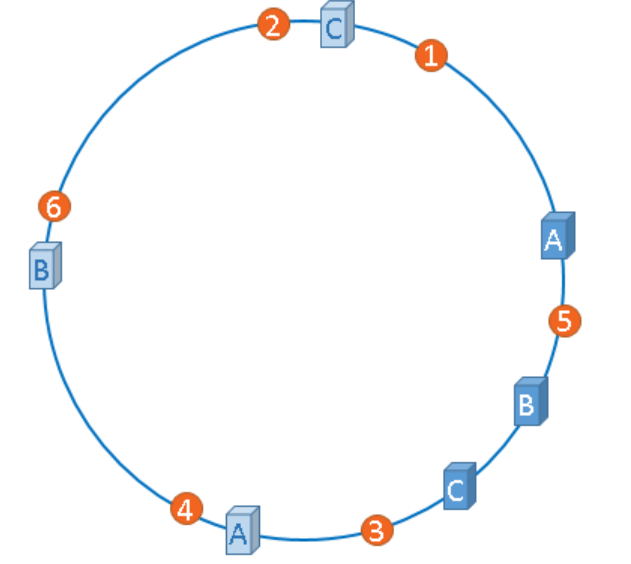
虚拟节点是“实际节点”(实际的物理服务器)在hash环上的复制品,一个实际节点可以对应多个虚拟节点。
从上图可以看出,A、B、C三台服务器分别虚拟出了一个虚拟节点,当然,如果你需要,也可以虚拟出更多的虚拟节点。引入虚拟节点的概念后,缓存的分布就均衡多了,上图中,1号、3号图片被缓存在服务器A中,5号、4号图片被缓存在服务器B中,6号、2号图片被缓存在服务器C中,如果你还不放心,可以虚拟出更多的虚拟节点,以便减小hash环偏斜所带来的影响,虚拟节点越多,hash环上的节点就越多,缓存被均匀分布的概率就越大。
问题:
公司让你做一个功能,在一个城市里面,有一个小人,小人可能站在这个城市的任何一个位置,怎么实现在小人方圆5公里内有哪些店推荐到手机上。假设每一家店都注册了自己的位置。
设计:
整个城市假设是大的网格,原点位置为中心,每隔一公里画一个块儿,每家店我们可以跟据经纬度对应一个格子。假设小人在某一个位置,x=29,y=17,那么我们可以找到他周围的格子,把里面的店做成一个list,最后计算一下每家店到小人的距离是不是小于5公里。
并行算法(了解)
岛问题
一个只有0和1俩种数字的二维矩阵中,上下左右能连成一片的1,算一个岛,返回矩阵中,一共有几个岛。下图中表示俩个岛。
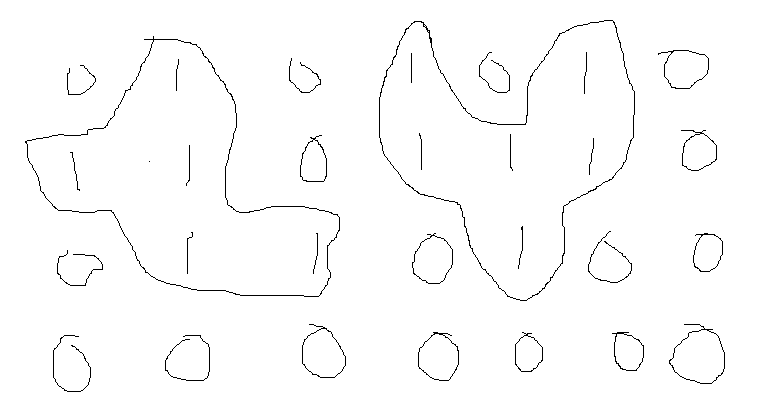
单CPU的函数代码O(N*M):
//主函数 public static int countIslands1(int[][] m) { if (m == null || m[0] == null) { return 0; } int N = m.length; int M = m[0].length; int res = 0; for (int i = 0; i < N; i++) { for (int j = 0; j < M; j++) { //如果是1,连成一片的1都会变成2,增加一个岛的数量,如果遇到一个感染过的点会跳过,有多少个不连成一片的1就有多少个岛 if (m[i][j] == 1) { res++; infect(m, i, j, N, M); } } } return res; } //单cpu的情况:感染函数infect,如果是1,把上下左右1所到之处全部感染成2,N多少行,M多少列 public static void infect(int[][] m, int i, int j, int N, int M) { if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] != 1) { return; } //跳出if时ij位置既不越界又是1 m[i][j] = 2; infect(m, i + 1, j, N, M); infect(m, i - 1, j, N, M); infect(m, i, j + 1, N, M); infect(m, i, j - 1, N, M); }
如果这个图很大,比如中国地图,那O(N*M)就会很大,这里用并行算法
假设有俩个cpu,矩阵中间被隔开,一个cpu负责左边的岛,一个cpu负责右边的岛,假设原本一共一个岛,左边求出2个,右边求出2个,利用并查集进行合并。同理,多个cpu负责不同的区域,最后利用并查集进行合并。
代码:
public static class Element<V> { public V value; public Element(V value) { this.value = value; } } public static class UnionFindSet<V> { // a -> a 生成的点 public HashMap<V, Element<V>> elementMap; public HashMap<Element<V>, Element<V>> fatherMap; // sizeMap中的key,每一个key都一定是集合的头节点(代表节点) public HashMap<Element<V>, Integer> sizeMap; public UnionFindSet(List<V> list) { elementMap = new HashMap<>(); fatherMap = new HashMap<>(); sizeMap = new HashMap<>(); for (V value : list) { Element<V> element = new Element<V>(value); elementMap.put(value, element); fatherMap.put(element, element); sizeMap.put(element, 1); } } // 从输入参数element出发,往上一直找,找到不能再往上的头节点,返回 private Element<V> findHead(Element<V> element) { // 把往上找的过程中,沿途的点都记录在path里 Stack<Element<V>> path = new Stack<>(); while (element != fatherMap.get(element)) { path.push(element); element = fatherMap.get(element); } while (!path.isEmpty()) { fatherMap.put(path.pop(), element); } return element; } //查询a与b是不是在一个集合 public boolean isSameSet(V a, V b) { if (elementMap.containsKey(a) && elementMap.containsKey(b)) { return findHead(elementMap.get(a)) == findHead(elementMap.get(b)); } return false; } //a的集合与b的集合合成一个大的集合 public void union(V a, V b) { if (elementMap.containsKey(a) && elementMap.containsKey(b)) { Element<V> aF = findHead(elementMap.get(a)); Element<V> bF = findHead(elementMap.get(b)); if (aF != bF) { Element<V> big = sizeMap.get(aF) >= sizeMap.get(bF) ? aF : bF; Element<V> small = big == aF ? bF : aF; fatherMap.put(small, big); sizeMap.put(big, sizeMap.get(aF) + sizeMap.get(bF)); sizeMap.remove(small); } } } public int getSetNum() { return sizeMap.size(); } } //主函数 public static int countIslands2(int[][] m) { List<String> list = new ArrayList<>(); for (int row = 0; row < m.length; row++) { for (int col = 0; col < m[0].length; col++) { if (m[row][col] == 1) { String position = String.valueOf(row) + "_" + String.valueOf(col); list.add(position); } } } UnionFindSet<String> unionSet = new UnionFindSet<>(list); for (int row = 0; row < m.length; row++) { for (int col = 0; col < m[0].length; col++) { if (m[row][col] == 1) { // row,col 5, 3 -> 5_3 String position = String.valueOf(row) + "_" + String.valueOf(col); if (row - 1 >= 0 && m[row - 1][col] == 1) { String up = String.valueOf(row - 1) + "_" + String.valueOf(col); unionSet.union(up, position); } if (col - 1 >= 0 && m[row][col - 1] == 1) { String left = String.valueOf(row) + "_" + String.valueOf(col - 1); unionSet.union(left, position); } } } } return unionSet.getSetNum(); }
Reference
白话解析 一致性哈希算法 consistent hashing
https://www.zsythink.net/archives/1182



 浙公网安备 33010602011771号
浙公网安备 33010602011771号