哈希函数有关的结构和岛问题

哈希函数

------>   out f（in data）

1.输入参数data，假设是in类型，特征：可能性无穷大，比如str类型的参数

2.输出参数out，特征：可能性可以很大，但一定是有穷尽的

3.哈希函数没有任何随机的机制，固定的输入一定是固定的输出

4.输入无穷多但输出值有限，所以不同输入也可能输出相同（哈希碰撞）

5.再相似的输入，得到的输出值，会几乎均匀的分布在out域上

重点：第五条

总结：

in ----> 无穷大  out ---> 有限   

没有任何随机成分  same in ---> same out

diff in ---> same out (哈希碰撞)

应用：

假设有一个40亿个整数的文件，每一个整数是4字节，文件里面一行就是一个整数，假设只有1G（byte字节）的内存，要统计哪一个数字出现的次数最多。

做法：1G内存做成哈希表，key(4字节)代表某个出现过的数，value(4字节)代表该数出现的次数，key，value无符号，一条记录占8字节。假设每个数字不一样，那就需要40亿条记录，共320亿字节(32G)才可以把记录全部装下，有可能让内存爆掉，所以不能这么做。1G内存大致能装10亿字节。

估算40亿/32G ~= 1亿，假设1G内存最多装1亿条记录。

利用hash函数，num1 ---f-->out1 ----> %40 --->0~39(假设是0)的数字，放在一个文件里面，num2 ---f-->out2 ----> %40 --->0~39(假设是1)的数字，放在另一个文件里面。这样，如果是同一个数字只会放在同一个文件里面，40亿个数字中，假设有S种不同的数，放在40个文件夹中不同数字的种数几乎均等，所以40个文件中几乎每个文件不会超过1亿条，我们只用1G内存放一个文件就可以了，先统计0号文件的词频，记录最大词频，然后释放内存，统计1号文件，记录最大词频。如果40亿数字一样，则out都一样，只需要放在0号文件中，只需要记录一条记录，value为40亿。

哈希表的实现

经典哈希表的实现

 

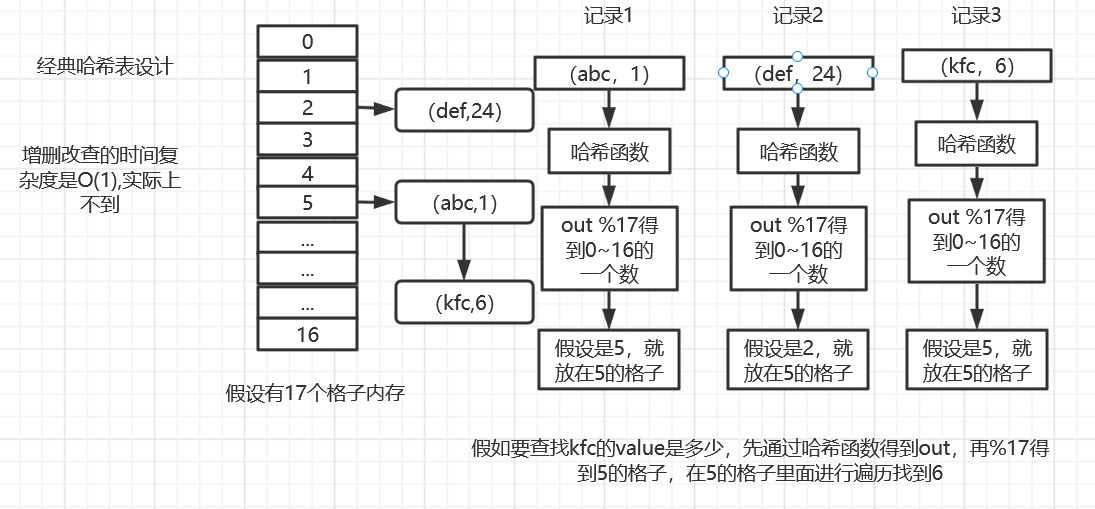
问题：空间太小，随着数据的增多，每个格子后面的单链表会变得很长，并且每个格子会均匀的分布。假设一个格子变成6，则可以认为其他格子都逼近6，假如格子数量变成2倍34个，则可以认为每个格子几乎会变成3。

总结：哈希表在使用时认为增删改查时间复杂度O(1)。

布隆过滤器

1.利用哈希函数的特质

2.每一条数据提取特征

3.加入扫黑库

应用场景：

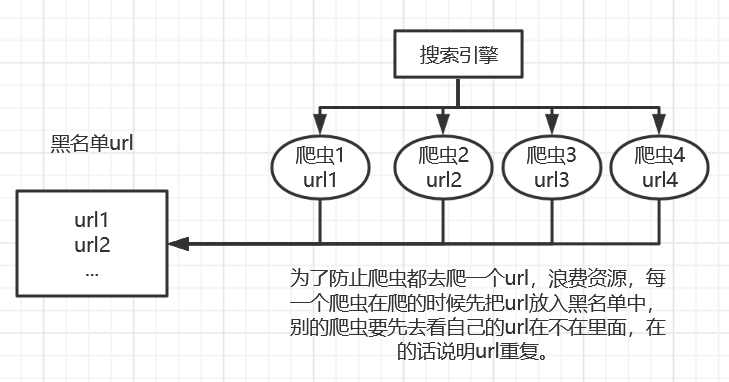
实现这个黑名单有很多种方法，比如哈希表。假设有100亿个url，每个url64字节，至少需要6400亿字节，大致640G内存空间。为了节省空间，利用布隆过滤器可以实现这个黑名单，内存不到30G。

• 在爬虫时，对爬虫网址进行过滤，已经存在布隆中的网址，不在爬取。
• 垃圾邮件过滤，对每个发送邮件的地址进行判断是否在布隆的黑名单中，若是在就判断为垃圾邮件。

大致原理

布隆过滤器上就是一个二进制数据的集合。

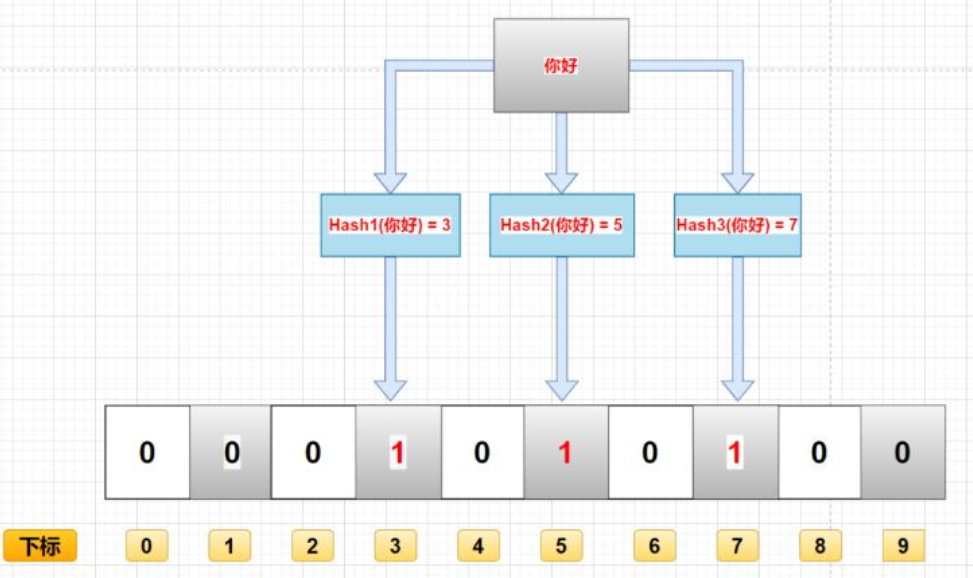
存入过程

当一个数据加入这个集合时，经历以下洗礼

• 经过K个哈希函数计算该数据，返回K个计算出的hash值
• 这些K个hash值映射到对应的K个二进制的数组下标
• 将K个下标对应的二进制数据改为1。

查询过程

布隆过滤器主要作用就是查询一个数据，在不在这个二进制的集合中，查询过程以下：

• 经过K个哈希函数计算该数据，对应计算出的K个hash值
• 经过hash值找到对应的二进制的数组下标
• 判断：若是存在一处位置的二进制数据是0，那么该数据不存在。若是都是1，该数据存在集合中。

优点：

• 因为存储的是二进制数据，因此占用的空间很小
• 它的插入和查询速度是很是快的，时间复杂度是O(K)，能够联想一下HashMap的过程
• 保密性很好，由于自己不存储任何原始数据，只有二进制数据

缺点：

添加数据是经过计算数据的hash值，那么可能存在这种状况：两个不一样的数据计算获得相同的hash值。

布隆过滤器重要的三个公式

1. 假设数据量为n，预期的失误率为p（布隆过滤器大小和每个样本的大小无关）
2. 跟据n和p，算出Bloom Filter一共需要多少个bit位，向上取整，记为m
3. 跟据m和n，算出Bloom Filter需要多少个哈希函数，向上取整，记为k
4. 跟据修正公式，算出真实的失误率p，带入理论的k与m到第三个公式

 

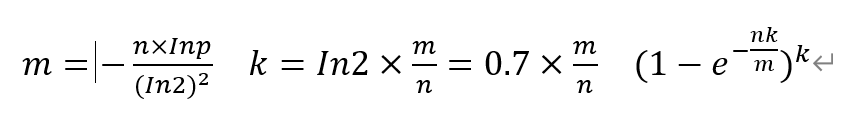
如何找到k个哈希函数？

事实上只需要找俩个哈希函数就够了，然后组合成k个哈希函数。假设找到哈希函数f与g，那么第一个哈希函数可以当作f()+1*g(),第二个哈希函数f()+2*g()，这样做每一个哈希函数都几乎独立，彼此无影响(来自左神一百亿布隆过滤器实操)。