数组累加和问题三连

问题1

数组arr[...]都是正数，问累加和=sum的子数组最长是多长，子数组连续，子串连续，子序列可以不连续

思路：

1.准备一个窗口，定义变量windowSum表示窗口内累加和，len要返回的子数组最大长度

2.windowSum < sum,R右移

3.windowSum > sum,L右移

4.windowSum = sum，更新len，R右移

只要一个指标可以跟数组的范围产生单调性，一定存在优化，要么双指针，要么窗口等

代码：

 //利用滑动窗口求累加和
    public static int getMaxLength(int[] arr, int sum) {
        if (arr == null || arr.length == 0 || sum <= 0) {
            return 0;
        }
        int left = 0;
        int right = 0;
        int windowSum = arr[0];//[0,0]
        int len = 0;
        while (right < arr.length) {
            if (windowSum == sum) {
                len = Math.max(len, right - left + 1);
                //窗口内的累加和减去left位置的值，left向右移动一位
                windowSum -= arr[left++];
            } else if (windowSum < sum) {
                right++;
                if (right == arr.length) {
                    break;
                }
                windowSum += arr[right];
            } else {
                windowSum -= arr[left++];
            }
        }
        return len;
    }

问题2

数组arr[...]有正数，负数，零，问累加和=k的子数组最长是多长

思路：

1.建立hashMap，key：前缀和   value：最早出现的位置

2. 0~i如果前缀和是1000，k=200，则直接找800最早出现的位置，len=i-hashmap.get(sum - k);

代码：

    public static int maxLength(int[] arr, int k) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        //key：前缀和 value：最早出现的位置
        HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
        //important：arr=[3,-3,7],k=7, map：（3，0），（0，1），（7，2），i=2的时候找前缀和为7-7的最早位置找到了1，所以一开始要加一个（0，-1）
        map.put(0, -1); 
        int len = 0;
        int sum = 0;//0~i的累加和
        for (int i = 0; i < arr.length; i++) {
            sum += arr[i];
            if (map.containsKey(sum - k)) {//0~i累加和1000，k=200，要找的是800最早出现的位置
                len = Math.max(i - map.get(sum - k), len);
            }
            if (!map.containsKey(sum)) {
                map.put(sum, i);
            }
        }
        return len;
    }

扩展问题：arr[...]中，有正数，负数，零，子数组中含有1的数量与含有2的数量一样多称为达标，问达标的子数组中最长的子数组的长度是多少

思路：将数组预处理，不是1与2的全部变成0，1变成1，2变成-1，求累加和是0的最长子数组。

问题3(superhard)

arr[...]中，有正数，负数，零，k是累加和，所有<=k的子数组都达标，问所有达标的子数组中最长长度是多少

思路图解：最优解时间复杂度O(N)

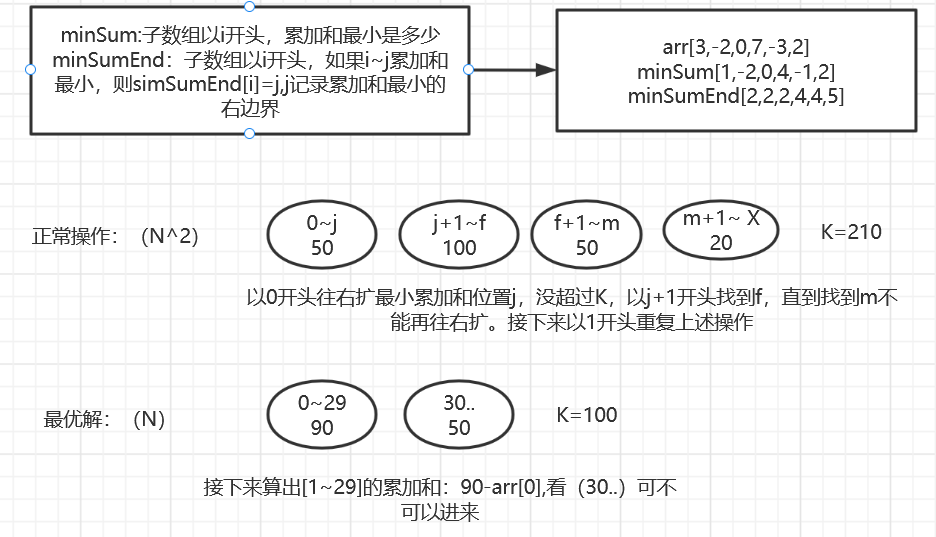
 代码：

public static int maxLengthAwesome(int[] arr, int k) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        int[] minSums = new int[arr.length];
        int[] minSumEnds = new int[arr.length];
        //minSums与minSumEnds的最后一个数，都不需要右扩
        minSums[arr.length - 1] = arr[arr.length - 1];
        minSumEnds[arr.length - 1] = arr.length - 1;
        //求minSums与minSumEnds
        for (int i = arr.length - 2; i >= 0; i--) {
            if (minSums[i + 1] <= 0) {//发现往右扩可以
                minSums[i] = arr[i] + minSums[i + 1];
                minSumEnds[i] = minSumEnds[i + 1];//minSumEnds[i]的右边界与i+1的右边界一样
            } else {//不能往右扩的情况那就是自己
                minSums[i] = arr[i];
                minSumEnds[i] = i;
            }
        }
        
        //(i...)(...)(...)(end...)i开始往右扩，end开始就大于k了
        int end = 0;
        //i.......end i~end的累加和
        int sum = 0;
        int len = 0;
        // i是窗口的最左的位置，end扩出来的最右有效块儿的最后一个位置的，再下一个位置
        // end也是下一块儿的开始位置
        // 窗口：[i~end)
        for (int i = 0; i < arr.length; i++) {
            // while循环结束之后：
            // 1) 如果以i开头的情况下，累加和<=k的最长子数组是arr[i..end-1]，看看这个子数组长度能不能更新res；
            // 2) 如果以i开头的情况下，累加和<=k的最长子数组比arr[i..end-1]短，更新还是不更新res都不会影响最终结果；
            while (end < arr.length && sum + minSums[end] <= k) {
                //(end...?) (?+1...
                sum += minSums[end];
                end = minSumEnds[end] + 1;
            }
            //结束while已经形成了[i...](end...X),i的大窗口可以，加上end这块不行。[i...]有多少个数：end - i
            len = Math.max(len, end - i);
            
            //求[i....] -> [i+1...]的累加和
            if (end > i) { // 窗口内还有数 [i~end) [4,4)
                sum -= arr[i];
            } else { // 窗口内已经没有数了，说明从i开头的所有子数组累加和都不可能<=k
                end = i + 1;
            }
        }
        return len;
    }