打表技巧和矩阵处理技巧

打表法

1.问题如果返回值不太多，可以用hardcode的方式列出，作为程序的一部分

2.一个大问题解决时底层频繁使用规模不大的小问题的解，如果小问题的返回值满足条件1，可以把小问题的解列成一张表，作为程序的一部分

3.打表找规律（重要）

打表找规律

1. 某个问题，输入参数类型简单，并且只有一个实际参数

2.要求的返回值类型也简单，并且只有一个

3.用暴力方法，把输入参数对应的返回值，打印出来看看，进而优化code

栗子1：

小虎去买苹果，商店只提供俩种类型的塑料袋，每种类型都有任意数量。

1.能装下6个苹果的塑料袋 2.能装下8个苹果的塑料袋

小虎可以自由使用俩种袋子来装苹果，但是小虎有强迫症，他要求自己使用的袋子数量必须最少，且使用的每个袋子必须装满。

给定一个正整数N，返回至少使用多少个袋子。如果N无法让使用的每个袋子必须装满，返回-1

代码：

//暴力解
    public static int minBags(int apple) {
        if (apple < 0) {
            return -1;
        }
        int bag6 = -1;
        int bag8 = apple / 8;
        int rest = apple - 8 * bag8;
        while (bag8 >= 0 && rest < 24) {
            int restUse6 = minBagBase6(rest);
            if (restUse6 != -1) {
                bag6 = restUse6;
                break;
            }
            rest = apple - 8 * (--bag8);
        }
        return bag6 == -1 ? -1 : bag6 + bag8;
    }

    // 如果剩余苹果rest可以被装6个苹果的袋子搞定，返回袋子数量
    // 不能搞定返回-1
    public static int minBagBase6(int rest) {
        return rest % 6 == 0 ? (rest / 6) : -1;
    }
    
    //O(1) 通过观察1~100返回值得出的规律
    public static int minBagAwesome(int apple) {
        if ((apple & 1) != 0) { // 如果是奇数，返回-1
            return -1;
        }
        //18之前
        if (apple < 18) {
            return apple == 0 ? 0 : (apple == 6 || apple == 8) ? 1
                    : (apple == 12 || apple == 14 || apple == 16) ? 2 : -1;
        }
        //18之后
        return (apple - 18) / 8 + 3;
    }

    public static void main(String[] args) {
        for(int apple = 1; apple < 100;apple++) {
            //先用暴力解来找规律
            System.out.println(apple + " : "+ minBags(apple));
        }

    }

栗子2：

给定一个正整数N，代表有N份青草统一堆放在仓库里，有一只牛和一只羊，牛先吃，🐏后吃，他俩轮流吃草。不管是牛还是羊，每一轮能吃草的数量必须是：

1，4，16，64...(4的某次方)，谁最先把草吃完谁获胜。假设牛和羊都绝顶聪明，都想赢，都会做出理性的决定，跟据唯一的参数N，返回谁会赢

代码：

 // n份青草放在一堆
        // 先手后手都绝顶聪明
        // string "先手" "后手"
        public static String winner1(int n) {
            // 0  1  2  3 4
            // 后 先 后 先 先
            if (n < 5) { // base case
                return (n == 0 || n == 2) ? "后手" : "先手";
            }
            // n >= 5 时
            int base = 1; // 当前先手决定吃的草数
            // 当前是先手在选
            while (base <= n) {
                // 当前一共n份草，先手吃掉的是base份，n - base 是留给后手的草
                // 母过程 先手 在子过程里是 后手
                //当我选择吃掉base，后续过程如果我能赢，则赢
                if (winner1(n - base).equals("后手")) {
                    return "先手";
                }
                if (base > (n / 4)) { // 防止base*4之后溢出
                    break;
                }
                base *= 4;
            }
            return "后手";
        }

        public static String winner2(int n) {
            if (n % 5 == 0 || n % 5 == 2) {
                return "后手";
            } else {
                return "先手";
            }
        }

        public static void main(String[] args) {
            for (int i = 0; i <= 50; i++) {
                System.out.println(i + " : " + winner1(i));
            }
        }

栗子3：

定义一个数：可以表示成若干（数量>1）连续正数和的数。比如：5=2+3 5就是这样的数，12=3+4+5，12就是这样的数。1不是这样的数，因为要求数量大于1个，连续正数和，2=1+1也不是，因为不是连续正数，给定一个参数N，返回是不是可以表示成若干连续正数和的数

    //暴力解  例如num=100，从1+2+3..，加到100返回true，超过100false，然后2+3+。。。尝试
    public static boolean isMSum1(int num) {
        for (int i = 1; i <= num; i++) { //开头的数
            int sum = i;
            for (int j = i + 1; j <= num; j++) {
                if (sum + j > num) {
                    break;
                }
                if (sum + j == num) {
                    return true;
                }
                sum += j;
            }
        }
        return false;
    }
    
    public static boolean isMSum2(int num) {
        if (num < 3) {
            return false;
        }
        
        //>3的情况4，8，16，32，64为false，其余为true，发现如果是2的次幂返回false，否则true
        //num & (num - 1)：判断num是不是2的某次幂， (num & (num - 1)) == 0 是2的某次方
        //2的某次方表示2进制只有一个1，该数-1表示将1之后的0全变成1，例如num=0001000，num-1=0000111
        //num&(num-1)==0则表示num是2的某次方
        return (num & (num - 1)) != 0;//不是2的某次放返回true
    }

    public static void main(String[] args) {
        for (int num = 1; num < 200; num++) {
            System.out.println(num + " : " + isMSum1(num));
        }
        
        System.out.println("test begin");
        for (int num = 1; num < 5000; num++) {
            if (isMSum1(num) != isMSum2(num)) {
                System.out.println("Oops!");
            }
        }
        System.out.println("test end");
    }

矩阵处理技巧

1. zigzag打印矩阵

核心技巧：找到coding上的宏观调度

zigzag矩阵图

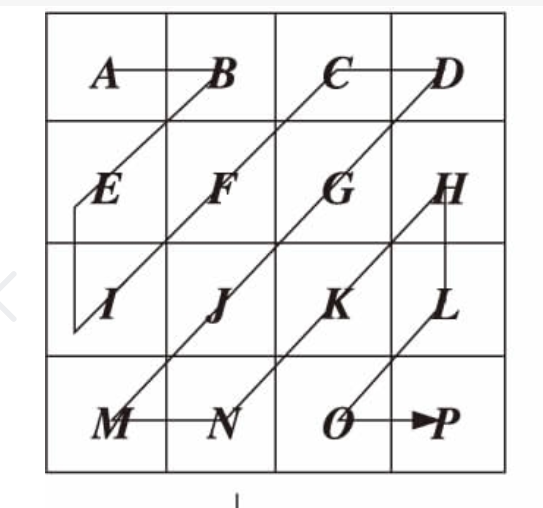
代码：

    public static void printMatrixZigZag(int[][] matrix) {
        int Ar = 0;
        int Ac = 0;
        int Br = 0;
        int Bc = 0;//初始位置A在0行0列，B在0行0列
        int endR = matrix.length - 1;//最后一行
        int endC = matrix[0].length - 1;//最后一列
        boolean fromUp = false;//是不是从右上往左下打印，一开始是左下往右上打印，所以是false
        while (Ar != endR + 1) {//endR + 1最后一行的再下一行
            //告诉你斜线的俩端是A跟B，以及方向，去打印
            printLevel(matrix, Ar, Ac, Br, Bc, fromUp);
            //A先向右走，不能往右就往下，B先往下走，不能往下就往右，不能换顺序，先动的要写在最后，边界问题
            Ar = Ac == endC ? Ar + 1 : Ar;//如果A的列到了最后一列，A的行号开始+1，否则不变
            Ac = Ac == endC ? Ac : Ac + 1;//如果A的列到了最后一列，A的列数不变，否则+1
            Bc = Br == endR ? Bc + 1 : Bc;//如果B的行数到了最后一行，B的列开始+1，否则不变
            Br = Br == endR ? Br : Br + 1;//如果B的行数到了最后一行，B的行号不变，否则+1
            fromUp = !fromUp;//打印方向每次取相反
        }
        System.out.println();
    }
     //打印的方向
    public static void printLevel(int[][] m, int tR, int tC, int dR, int dC,
            boolean f) {
        if (f) {
            //右上往左下打印
            while (tR != dR + 1) {
                System.out.print(m[tR++][tC--] + " ");
            }
        } else {
            //左下往右上打印
            while (dR != tR - 1) {
                System.out.print(m[dR--][dC++] + " ");
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 } };
        //1 2 5 9 6 3 4 7 10 11 8 12 
        printMatrixZigZag(matrix);
    }

转圈打印矩阵（顺时针转圈）

核心技巧：找到coding上的宏观调度

代码：

public static void spiralOrderPrint(int[][] matrix) {
        //左上角点行跟列
        int tR = 0;
        int tC = 0;
        //右下角点行跟列
        int dR = matrix.length - 1;
        int dC = matrix[0].length - 1;
        
        while (tR <= dR && tC <= dC) {
            //左上角点往右下移动，右下角点往左上移动
            printEdge(matrix, tR++, tC++, dR--, dC--);
        }
    }
    //左上角位置a，b 右下角位置c，d
    public static void printEdge(int[][] m, int a, int b, int c, int d) {
        if (a == c) {
            for (int i = b; i <= d; i++) {
                System.out.print(m[a][i] + " ");//最后只剩下一条横线，打印一条横线
            }
        } else if (b == d) {
            for (int i = a; i <= c; i++) {
                System.out.print(m[i][b] + " ");//最后只剩下一条竖线，打印一条竖线
            }
        } else {
            int curC = b;
            int curR = a;
            while (curC != d) {
                System.out.print(m[a][curC] + " ");
                curC++;
            }
            while (curR != c) {
                System.out.print(m[curR][d] + " ");
                curR++;
            }
            while (curC != b) {
                System.out.print(m[c][curC] + " ");
                curC--;
            }
            while (curR != a) {
                System.out.print(m[curR][b] + " ");
                curR--;
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
                { 13, 14, 15, 16 } };
        //1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10 
        spiralOrderPrint(matrix);
    }

原地旋转正方形矩阵

核心技巧：找到coding上的宏观调度

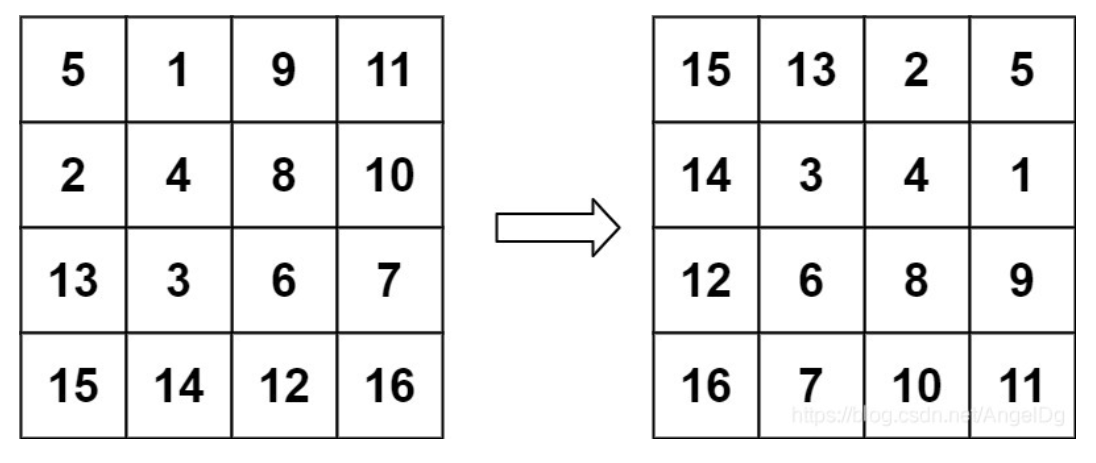
 代码：

    public static void rotate(int[][] matrix) {
        //左上角点行跟列
        int a = 0;
        int b = 0;
        //右下角点行跟列
        int c = matrix.length - 1;
        int d = matrix[0].length - 1;
        while (a < c) {
            rotateEdge(matrix, a++, b++, c--, d--);
        }
    }

    public static void rotateEdge(int[][] m, int a, int b, int c, int d) {
        int tmp = 0;
        //i表示有组号，7*7最外面一层一共6组，4个数字表示一组
        for (int i = 0; i < d - b; i++) {
            //m[a][b + i]表示每个小组的第一个点, m[a + i][d]每个小组第二个点 m[c][d - i] 每个小组第三个点 m[c - i][b]每个小组第四个点
            //四个点互换位置
            tmp = m[a][b + i];
            m[a][b + i] = m[c - i][b];
            m[c - i][b] = m[c][d - i];
            m[c][d - i] = m[a + i][d];
            m[a + i][d] = tmp;
        }
    }
    //打印矩阵
    public static void printMatrix(int[][] matrix) {
        for (int i = 0; i != matrix.length; i++) {
            for (int j = 0; j != matrix[0].length; j++) {
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 }, { 13, 14, 15, 16 } };
        printMatrix(matrix);
        rotate(matrix);
        System.out.println("=========");
        printMatrix(matrix);
        /*
         * 1 2 3 4 
           5 6 7 8 
           9 10 11 12 
           13 14 15 16 
           =========
           13 9 5 1 
           14 10 6 2 
           15 11 7 3 
           16 12 8 4 
         */

    }