Morris遍历及其相关扩展

Morris遍历

morris遍历是二叉树遍历算法的超强进阶算法，跟递归、非递归（栈实现）的空间复杂度，morris遍历可以将非递归遍历中的空间复杂度降为O(1)。从而实现时间复杂度为O(N)，而空间复杂度为O(1)的精妙算法。
morris遍历利用的是树的叶节点左右孩子为空（树的大量空闲指针），实现空间开销的极限缩减。

步骤：

当前节点cur一开始来到root

1.如果cur无左树，cur=cur.right

2.如果cur有左树，找到左树最右的节点，极为mostright

2.1 mostright的右指针指向null, mostright.right = cur; cur = cur.left;

2.2 mostright的右指针指向当前节点cur，mostright.right = null; cur = cur.right;

图解：

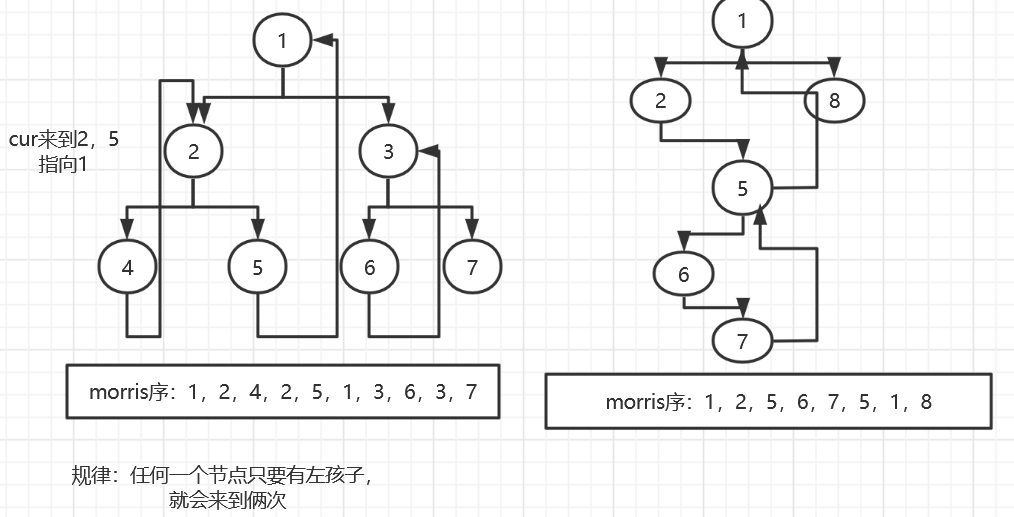
 图1：

1）首先cur来到头结点1，按照morris原则的第二条第一点，它存在左孩子，cur左子树上最右的节点为5，它的right指针指向空，所以让其指向1，cur向左移动到2。

2）2有左孩子，且它左子树最右的节点4指向空，按照morris原则的第二条第一点,让4的right指针指向2，cur向左移动到4

3）4不存在左孩子，按照morris原则的第一条，cur向右移动，在第二步中，4的right指针已经指向了2，所以cur会回到2

4）重新回到2，有左孩子，它左子树最右的节点为4，但是在第二步中，4的right指针已经指向了2，不为空。所以按照morris原则的第二条第二点，2向右移动到5，同时4的right指针重新指向空

5）5不存在左孩子，按照morris原则的第一条，cur向右移动，在第一步中，5的right指针已经指向了1，所以cur会回到1

6）cur回到1，回到头结点，左子树遍历完成，1有左孩子，左子树上最右的节点为5，它的right指针指向1，按照morris原则的第二条第二点，1向右移动到3，同时5的right指针重新指回空

……

当到达最后一个节点7时，按照流程下来，此时7无左右孩子，遍历结束。

代码：

    public static class Node {
        public int value;
        Node left;
        Node right;

        public Node(int data) {
            this.value = data;
        }
    }
    public static void morris(Node head) {
        if (head == null) {
            return;
        }
        
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            //1.cur有没有左树，
            mostRight = cur.left;
            //有左树
            if (mostRight != null) { 
                //有左树的情况下，先找到左树的真实的最右节点
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                //从while中出来，mostright一定是cur左树上的最右节点
                //mostroght指向空的情况下，
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue; //while的continue
                } else {//mostRight.right = null; --->  mostRight.right == cur
                    mostRight.right = null;
                    cur = cur.right;
                    continue; 
                }
            }
            //没有左树，cur右移
            cur = cur.right;
        }
    }

 Morris遍历转先序遍历：

2次出现的数字第一次出现打印，1次出现的数字直接打印

 //morrios序转先序遍历：2次出现的数字第一次出现打印
    public static void morrisPre(Node head) {
        if (head == null) {
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    //能回到自己俩次的节点第一次到的时候打印
                    System.out.print(cur.value + " ");
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                }
            } else {
                //没有左树就打印，else代表只到达一次的节点
                System.out.print(cur.value + " ");
            }
            cur = cur.right;
        }
        System.out.println();
    }

Morris遍历转中序遍历：

2次出现的数字第二次出现打印，一次出现的数字直接打印

  //morrios序转中序遍历：2次出现的数字第二次出现打印
    public static void morrisIn(Node head) {
        if (head == null) {
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                }
            }
            //总结，只要往右移动就打印
            System.out.print(cur.value + " ");
            cur = cur.right;
        }
        System.out.println();
    }

Morris遍历转后序遍历：

能回到自己俩次，第二次到的时候逆序打印左树的右边界

 

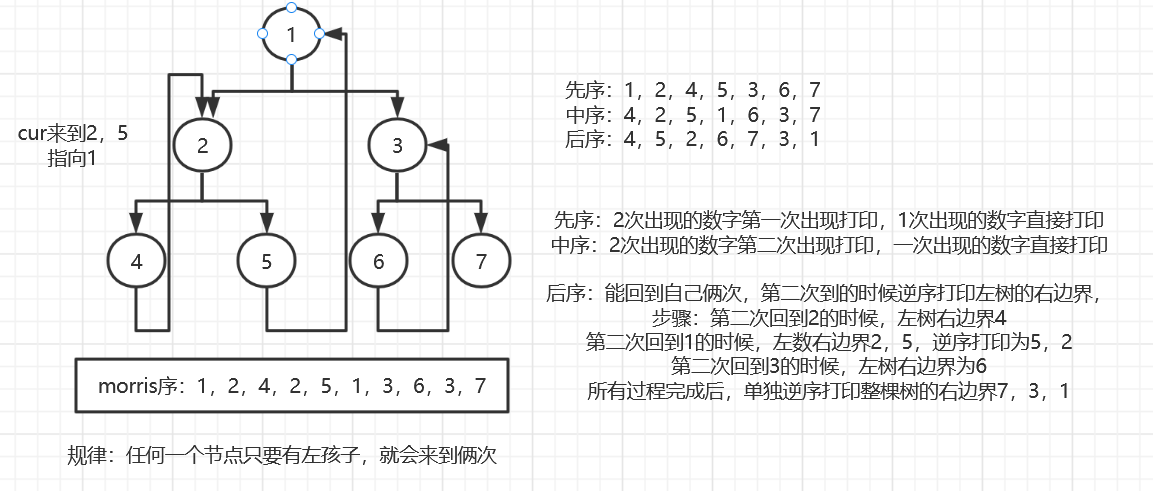
 代码：

//morrios序转后序遍历：能回到自己俩次，第二次回到自己的时候逆序打印左树的右边界
    public static void morrisPos(Node head) {
        if (head == null) {
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                    //能回到自己俩次，第二次回到自己的时候逆序打印左树的右边界
                    printEdge(cur.left);
                }
            }
            cur = cur.right;
        }
        //正颗树的右边界
        printEdge(head);
        System.out.println();
    }
    //逆序打印某个树的右边界
    public static void printEdge(Node head) {
        Node tail = reverseEdge(head);
        Node cur = tail;
        while (cur != null) {
            System.out.print(cur.value + " ");
            cur = cur.right;
        }
        reverseEdge(tail);
    }
    //，逆序链表，并返回头节点
    public static Node reverseEdge(Node from) {
        Node pre = null;
        Node next = null;
        while (from != null) {
            next = from.right;
            from.right = pre;
            pre = from;
            from = next;
        }
        return pre;
    }

Morris遍历判断是否是搜索二叉树

   //利用morris遍历判断是否是搜索二叉树，中序遍历递增就是搜索二叉树
  //搜索二叉树，左边比我小，右边比我大
    public static boolean isBST(Node head) {
        if (head == null) {
            return true;
        }
        Node cur = head;
        Node mostRight = null;
        Integer pre = null;
        boolean ans = true;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                }
            }
            //如果不是递增
            if (pre != null && pre >= cur.value) {
                ans = false;
            }
            pre = cur.value;
            cur = cur.right;
        }
        return ans;
    }

栗子：

有一个树，求最小高度。最小高度：到了叶节点会有一个高度，返回所有叶节点中的最小的高度

递归：

    public static int minHeight1(Node head) {
        if (head == null) {
            return 0;
        }
        return p(head);
    }

    // 返回x为头的树，最小深度是多少
    public static int p(Node x) {
        if (x.left == null && x.right == null) {
            return 1;
        }
        // 左右子树起码有一个不为空
        int leftH = Integer.MAX_VALUE;
        if (x.left != null) {
            leftH = p(x.left);
        }
        int rightH = Integer.MAX_VALUE;
        if (x.right != null) {
            rightH = p(x.right);
        }
        return 1 + Math.min(leftH, rightH);
    }

Morros遍历：

    // 根据morris遍历改写
    public static int minHeight2(Node head) {
        if (head == null) {
            return 0;
        }
        Node cur = head;
        Node mostRight = null;
        int curLevel = 0;
        int minHeight = Integer.MAX_VALUE;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                int rightBoardSize = 1;
                while (mostRight.right != null && mostRight.right != cur) {
                    rightBoardSize++;
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) { // 第一次到达
                    curLevel++;
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else { // 第二次到达
                    if (mostRight.left == null) {
                        minHeight = Math.min(minHeight, curLevel);
                    }
                    curLevel -= rightBoardSize;
                    mostRight.right = null;
                }
            } else { // 只有一次到达
                curLevel++;
            }
            cur = cur.right;
        }
        int finalRight = 1;
        cur = head;
        while (cur.right != null) {
            finalRight++;
            cur = cur.right;
        }
        if (cur.left == null && cur.right == null) {
            minHeight = Math.min(minHeight, finalRight);
        }
        return minHeight;
    }