从暴力递归到动态规划(二)
常见的尝试模型
- 从左往右的尝试模型
- 范围上的尝试模型
- 多样本位置全对应的尝试模型
- 寻找业务限制的尝试模型
从左往右的尝试模型
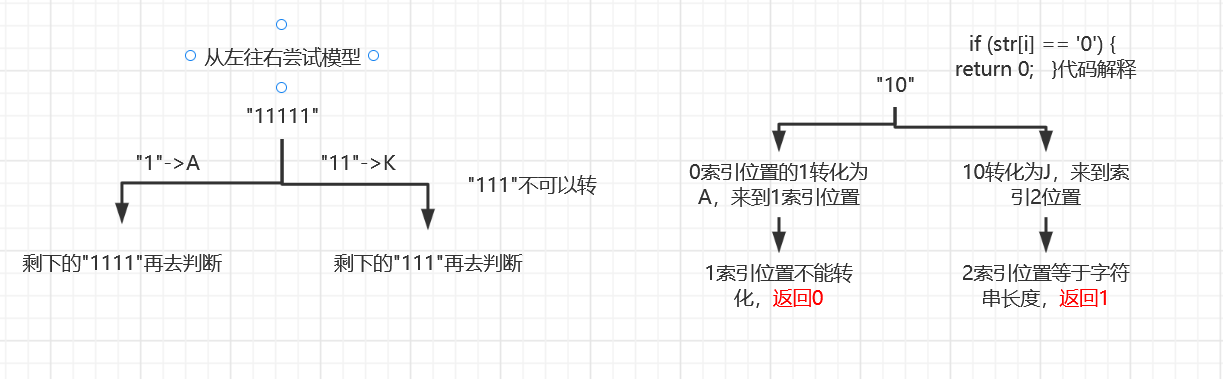
栗子1
规定1和A对应,2和B对应,以此类推。111->AAA,KA,AK,给定一个只有数字字符组成的字符串str,有多少种转化方式
图解:
代码暴力递归:
//str只含有数字字符0~9,返回多少种转化方案 public static int number(String str) { if (str == null || str.length() == 0) { return 0; } return process(str.toCharArray(), 0); } // str[0..i-1]转化无需过问 // str[i.....]去转化,返回有多少种转化方法 public static int process(char[] str, int i) { if (i == str.length) { return 1; } // 0没办法单独转化。例如10,1. 1->A,'0'不能转, 2.10->k if (str[i] == '0') { //之前的决定有问题 return 0; } // str[i] != '0' if(str[i] == '1') { //作为自己单独的部分,后续有多少种 int res = process(str, i+1); if(i+1 < str.length) { //(i和i+1)作为单独的部分,后续有多少种 res += process(str, i+2); } return res; } if(str[i] == '2') { int res = process(str, i+1); if( i + 1 < str.length && (str[i+1] >= '0' &&str[i+1] <= '6')) { res += process(str, i+2); } return res; } //i位置3~9没得选择,直接跳到i+1 return process(str, i+1); }
代码动态规划:
public static int dp1(String s) { if (s == null || s.length() == 0) { return 0; } char[] str = s.toCharArray(); int N = str.length; int[] dp = new int[N + 1]; dp[N] = 1; //通过观察已知dp[N],要求dp[0],i与i+1相关i+2,所以从后往前遍历.return的全部改成dp[],最后只需要返回dp[0]就可以了 for (int i = N - 1; i >= 0; i--) {
if (str[i] == '0') {
dp[i] = 0;
} else if (str[i] == '1') {
dp[i] = dp[i + 1];
if (i + 1 < N) {
dp[i] += dp[i + 2];
}
} else if (str[i] == '2') {
dp[i] = dp[i + 1];
if (i + 1 < str.length && (str[i + 1] >= '0' && str[i + 1] <= '6')) {
dp[i] += dp[i + 2];
}
} else {
dp[i] = dp[i + 1];
}
}
return dp[0]; }
栗子2
给定两个长度都为N的数组weights和values,weight[i]和values[i]分别代表物品的重量和价值,给定一个正数bag,表示一个载重的袋子,你装的物品不能超过这个重量,返回可以装下的最多的价值
代码暴力递归:
//w:重量 V:价值 //bag:背包容量,不能超过这个载重 //返回:不超重的情况下,能够得到的最大价值 public static int maxValue(int[] w, int[] v, int bag) { if (w == null || v == null || w.length != v.length || w.length == 0) { return 0; } // 尝试函数! return process(w, v, 0, bag); } //rest:还剩余的空间重量 public static int process(int[] w, int[] v, int index, int rest) { //没空间了 if (rest < 0) { return -1; } //没货了 if (index == w.length) { return 0; } //第一种可能性,不要当前货物 int p1 = process(w, v, index + 1, rest); int p2 = 0; //要了index位置的货物 int next = process(w, v, index + 1, rest - w[index]); if (next != -1) { p2 = v[index] + next; } return Math.max(p1, p2); }
代码动态规划:
public static int dp(int[] w, int[] v, int bag) { if (w == null || v == null || w.length != v.length || w.length == 0) { return 0; } int N = w.length; //做表格表示可变参数index与rest,横轴rest,纵轴index,然后按照暴力递归的代码在里面填值 int[][] dp = new int[N + 1][bag + 1]; //按照表格的范围 for (int index = N - 1; index >= 0; index--) { for (int rest = 0; rest <= bag; rest++) { //完全按照暴力递归的代码改成动态规划 int p1 = dp[index + 1][rest]; int p2 = 0; //rest=0会越界 if(rest - w[index] >= 0) { p2 = v[index] + dp[index + 1][rest - w[index]]; } dp[index][rest] = Math.max(p1, p2); } } return dp[0][bag]; }
范围上的尝试模型
栗子1
给定一个整数数组arr,代表数值不同的纸牌排成一条线,玩家A和玩家B依次拿走每张纸牌,规定玩家A先拿,玩家B后拿。但是每个玩家每次只能拿走最左或最右的纸牌,请返回最后获胜者的分数。
图解:

代码暴力递归:
//根据规则,返回获胜者的分数 public static int win1(int[] arr) { if (arr == null || arr.length == 0) { return 0; } //先手在数组位置上与后手在数组位置上谁大谁获胜 int first = f1(arr, 0, arr.length - 1); int second = g1(arr, 0, arr.length - 1); return Math.max(first, second); } // arr[L..R],先手获得的最好分数返回 public static int f1(int[] arr, int L, int R) { if (L == R) { return arr[L]; } int p1 = arr[L] + g1(arr, L + 1, R);//先拿左侧排 int p2 = arr[R] + g1(arr, L, R - 1);//先拿右侧排 return Math.max(p1, p2); } // // arr[L..R],后手获得的最好分数返回 public static int g1(int[] arr, int L, int R) { if (L == R) { return 0; } int p1 = f1(arr, L + 1, R); // 对手先拿走了L位置的数 int p2 = f1(arr, L, R - 1); // 对手先拿走了R位置的数 return Math.min(p1, p2);//对手帮选的肯定是最小的 }
代码动态规划:
//f与s是互相依赖的,都是N*N的表,f对角线是arr[i],s对角线是0,要求每张表的上半部分,下半部分L>R无效 public static int win2(int[] arr) { if (arr == null || arr.length == 0) { return 0; } int N = arr.length; int[][] f = new int[N][N]; int[][] s = new int[N][N]; //对应f里面的L==R,s没有,因为初始化就是0 for(int i = 0; i < N; i ++) { f[i][i] = arr[i]; } //求上半部分,f的上半部分依赖s,反之亦然。 for(int i = 1; i < N; i ++) { int L =0; int R = i; while(L < N && R < N) { //直接将return的内容换成数组里面 f[L][R] =Math.max(arr[L] +s[L + 1][R], arr[R] + s[L][R-1]); s[L][R] =Math.min(f[L+1][R], f[L][R-1]); //表里面的斜线 L ++; R ++; } } //最后我们要的是0~N-1的位置 return Math.max(f[0][N-1],s[0][N-1]); }
多样本位置全对应的尝试模型
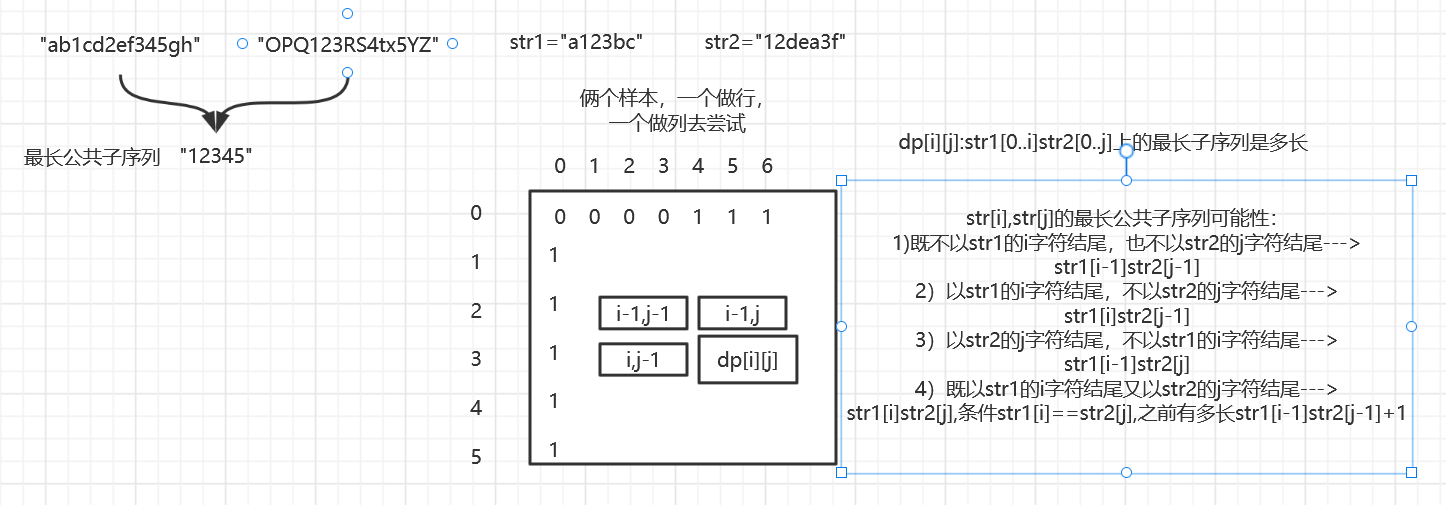
栗子:求俩个字符串的最长公共子序列
图解:
代码暴力递归:
public static int longestCommonSubsequence1(String s1, String s2) { if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) { return 0; } char[] str1 = s1.toCharArray(); char[] str2 = s2.toCharArray(); // 尝试 return process1(str1, str2, str1.length - 1, str2.length - 1); } public static int process1(char[] str1, char[] str2, int i, int j) { if (i == 0 && j == 0) { return str1[i] == str2[j] ? 1 : 0; } else if (i == 0) { if (str1[i] == str2[j]) { return 1; } else { return process1(str1, str2, i, j - 1); } } else if (j == 0) { if (str1[i] == str2[j]) { return 1; } else { return process1(str1, str2, i - 1, j); } } else { // i != 0 && j != 0 int p1 = process1(str1, str2, i - 1, j); int p2 = process1(str1, str2, i, j - 1); int p3 = str1[i] == str2[j] ? (1 + process1(str1, str2, i - 1, j - 1)) : 0; return Math.max(p1, Math.max(p2, p3)); } }
代码动态规划:
public static int longestCommonSubsequence2(String s1, String s2) { if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) { return 0; } char[] str1 = s1.toCharArray(); char[] str2 = s2.toCharArray(); int N = str1.length; int M = str2.length; int[][] dp = new int[N][M]; dp[0][0] = str1[0] == str2[0] ? 1 : 0; //填第0行的所有值,一旦找到str1的字符,后面的字符全是1 for (int j = 1; j < M; j++) { dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j - 1]; } //填写第0列的所有值,以str2的j结尾,不以str1的i结尾,一旦找到str2的字符,下面的字符全是1 for (int i = 1; i < N; i++) { dp[i][0] = str1[i] == str2[0] ? 1 : dp[i - 1][0]; } //任意位置dp[i][j] for (int i = 1; i < N; i++) { for (int j = 1; j < M; j++) { //可能性3 int p1 = dp[i - 1][j]; //可能性2 int p2 = dp[i][j - 1]; //可能性4 int p3 = str1[i] == str2[j] ? (1 + dp[i - 1][j - 1]) : 0; //三种可能性求max dp[i][j] = Math.max(p1, Math.max(p2, p3)); } } return dp[N - 1][M - 1]; }
什么暴力递归可以继续优化
有重复调用同一个子问题的解,这种递归可以优化
如果每一个子问题的解都是不同的解,无法优化
栗子
假设有排成一行的N个位置,记为1~N,N>=2。开始机器人在M位置上(M->1~N)。
如果机器人来到1位置,那么下一步只能往右来到2位置。
如果机器人来到N位置,那么下一步只能往左来到N-1置。
如果机器人来到中间位置,那么下一步可以往左或往右走。
规定机器人必须走K步,最终能来到P位置的方法有多少种?
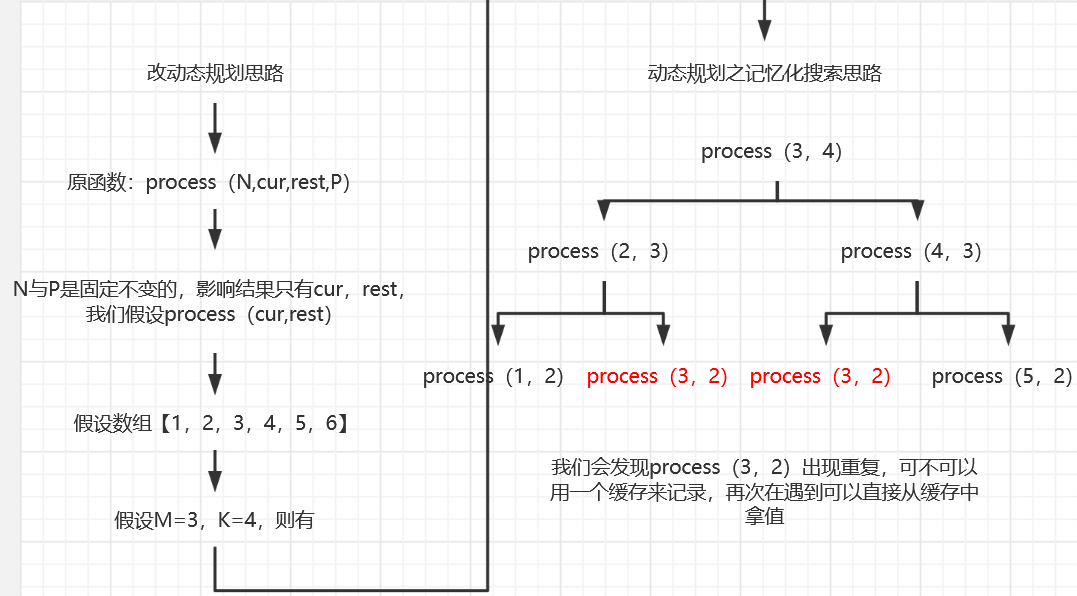
例如【1,2,3,4,5,6,7】 N= 7,M= 3, P=2, K=3 ,从3走到2走3步有三种。第一种: 3->2->3->2 第二种: 3->2->1->2 第三种: 3->4->3->2
实现方法:
1.暴力递归
2.暴力递归+缓存 ---> 动态规划,没有关心状态依赖,属于记忆性搜索,只要遇到重复计算就放入缓存中,缓存有很多数据结构可以实现
图解:
代码暴力递归
public static int way1(int N,int M,int K,int P) { if(N < 2 || K <1 || M <1 || M > N || P <1 || P > N) { return 0; } return walk1(N,M,K,P); } // N:一共多少位置 cur:当前位置 rest:剩余多少步数 P:最终目标位置 public static int walk1(int N,int cur,int rest,int P) { // 没有步数走完了 if(rest == 0) { return cur == P?1:0; } // 在1位置只能往右走 if(cur == 1) { return walk1(N, 2, rest -1, P); } // 在N位置只能往左走 if(cur == N) { return walk1(N, N-1, rest -1, P); } //中间位置可以往左也可以往右 return walk1(N, cur + 1, rest -1, P) + walk1(N, cur -1, rest -1, P); }
代码动态规划
public static int wayChahe(int N,int M,int K,int P) { if(N < 2 || K <1 || M <1 || M > N || P <1 || P > N) { return 0; } //建立缓存数组,初始化为-1 int[][] dp = new int[N+1][K+1]; for(int row = 0; row <= N; row ++) { for(int col = 0;col <= K; col ++) { dp[row][col] = -1; } } return walk1(N,M,K,P); } public static int walkCache(int N,int cur,int rest,int P,int[][] dp) { //之前dp[cur][rest]算过了,可以直接返回,后面在返回前全部存到数组里 if(dp[cur][rest] != -1) { return dp[cur][rest]; } // 没有步数走完了 if(rest == 0) { dp[cur][rest] = cur == P?1:0; return dp[cur][rest]; } // 在1位置只能往右走 if(cur == 1) { dp[cur][rest] = walkCache(N, 2, rest -1, P,dp); return dp[cur][rest]; } // 在N位置只能往左走 if(cur == N) { dp[cur][rest] = walkCache(N, N-1, rest -1, P,dp); return dp[cur][rest]; } //中间位置可以往左也可以往右 dp[cur][rest] = walkCache(N, cur + 1, rest -1, P,dp) + walkCache(N, cur -1, rest -1, P,dp); return dp[cur][rest]; }
总结:
这一节介绍了三种尝试的模型,一种是从左往右的尝试模型,举了俩个例子,数字字符转字符串与背包可以装下价值最大化问题。一种是范围上的尝试模型,举例了最后获胜者分数的例子。第三种是多样本位置全对应的尝试模型,这几个例子我们都是采用了暴力递归的尝试方法与动态规划去做的,暴力递归最贴近我们的自然智慧,也比较容易想到,但效率却很低下。我们还列举了一个机器人走路的问题,利用了在暴力递归过程中加入一个缓存,将有重复计算的值放入到缓存中,下次我们再用的时候就可以直接从缓存中拿值,这其实就是动态规划里面的记忆化搜索,并没有关心每一个状态的依赖,只是单纯的存储,拿值,这样已经大大的提高了我们的效率。
注意点:
任何一个动态规划都是由暴力递归的尝试改过来的,只要我们可变参数有限几个,就可以改成动态规划。
难点在于尝试过程,状态转移方程是尝试过程的抽象化的表达,只有尝试过程明白了才可以写出状态转移,所以要先建立递归的感觉。
没有重复子过程就不需要改动态规划,是否存在重复子过程有经验可以直接看出来,没经验可以举例子列举一下
dp就是暴力递归的过程想办法把返回值放在一张表里,如果主问题需要求0状态的答案就返回dp[0],如果N状态的答案就dp[N]。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号