从暴力递归到动态规划(一)

暴力递归

基本介绍：

1. 把问题转化为规模缩小了的同类子问题
2. 有明确的不需要继续进行的递归的条件
3. 有当得到了子问题的结果之后的决策过程
4. 不记录每一个子问题的解

栗子1

       实现逆序一个栈，不能申请额外的数据结构，只能使用递归函数。

思路：f函数返回栈底元素，并将剩余元素盖下去

图解：

 

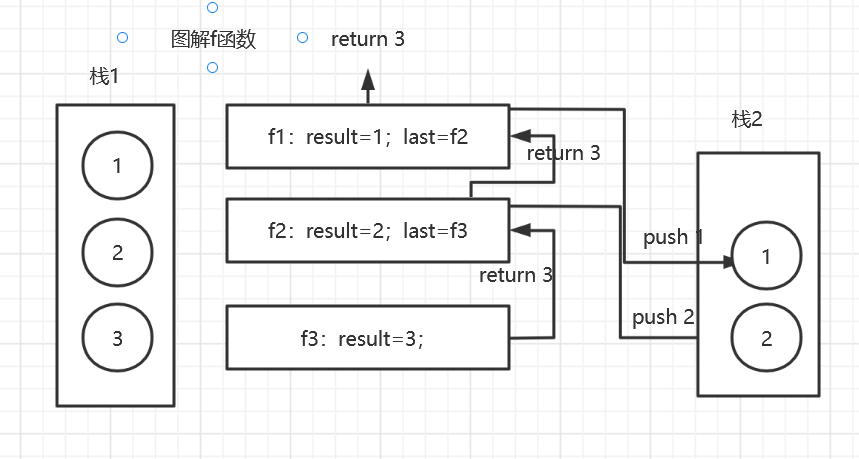
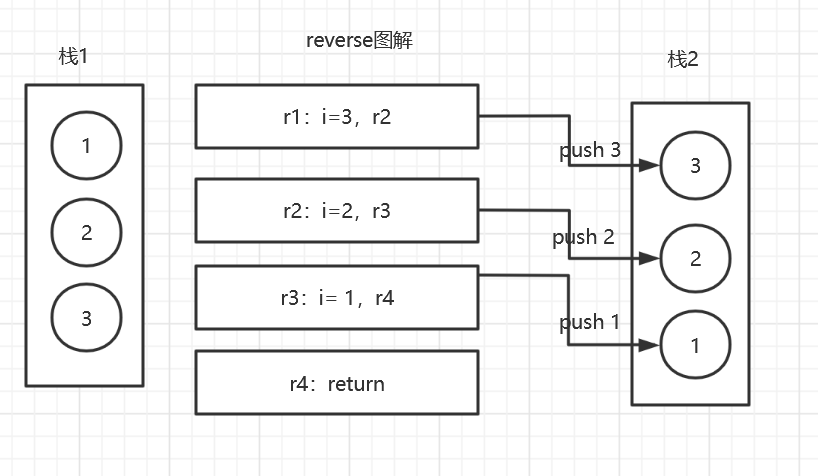
 代码：

public static void reverse(Stack<Integer> stack) {
        if (stack.isEmpty()) {
            return;
        }
        int i = f(stack);
        reverse(stack);
        stack.push(i);
    }
    // 返回栈底元素
    // 上面的元素盖下来
    public static int f(Stack<Integer> stack) {
        int result = stack.pop();
        if (stack.isEmpty()) {
            return result;
        } else {
            int last = f(stack);
            stack.push(result);
            return last;
        }
    }

任何一个动态规划问题都是某一个暴力尝试优化后的结果，所以在介绍动态规划之前我们先来了解一下如何利用暴力递归来进行尝试？

熟悉什么叫尝试？

栗子1

 打印一个字符串的全部子序列

图解：

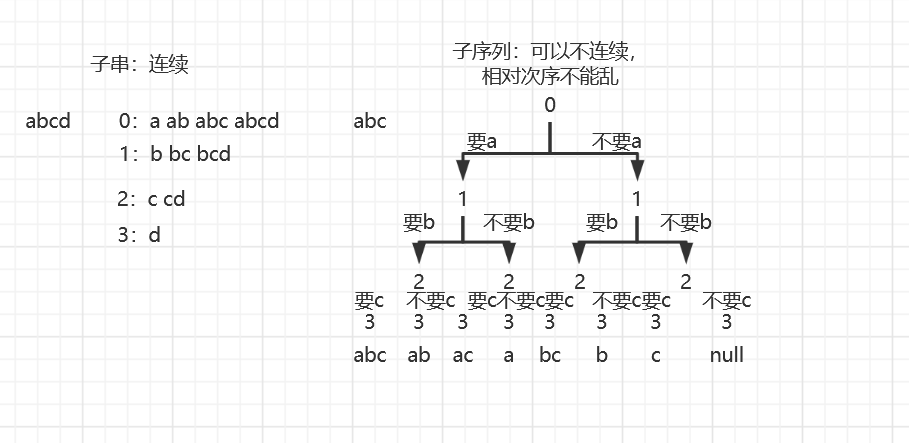
代码：

    public static List<String> subs(String s) {
            char[] str = s.toCharArray();
            String path = "";
            List<String> ans = new ArrayList<>();
            process1(str, 0, ans, path);
            return ans;
        }
        
        //当前字符串转化成的数组
        //index位置索引
        // path：str[0..index-1]已经走过的路径
        // ans：已经生成好的子序列
        public static void process1(char[] str, int index, List<String> ans, String path) {
            if (index == str.length) {
                ans.add(path);
                return;
            }
            // 没有要index位置的字符
            String no = path;
            process1(str, index + 1, ans, no);
            // 要了index位置的字符
            String yes = path + String.valueOf(str[index]);
            process1(str, index + 1, ans, yes);
        }

栗子2

打印一个字符串的全部子序列，要求不要出现重复字面值的子序列

思路：

           1.可以利用HashSet不允许重复的属性

           2.可以先将子序列全部列出来，然后去重复

代码：

    //打印一个字符串的全部子序列，要求不要出现重复字面值的子序列
        public static List<String> subsNoRepeat(String s) {
            char[] str = s.toCharArray();
            String path = "";
            HashSet<String> set = new HashSet<>();
            //将子序列都放入到了set中
            process2(str, 0, set, path);
            //将Set集合转化成List
            List<String> ans = new ArrayList<>();
            for (String cur : set) {
                ans.add(cur);
            }
            return ans;
        }
        public static void process2(char[] str, int index, HashSet<String> set, String path) {
            if (index == str.length) {
                set.add(path);
                return;
            }
            String no = path;
            process2(str, index + 1, set, no);
            String yes = path + String.valueOf(str[index]);
            process2(str, index + 1, set, yes);
        }

栗子3

    打印一个字符串的全部排列

 图解：

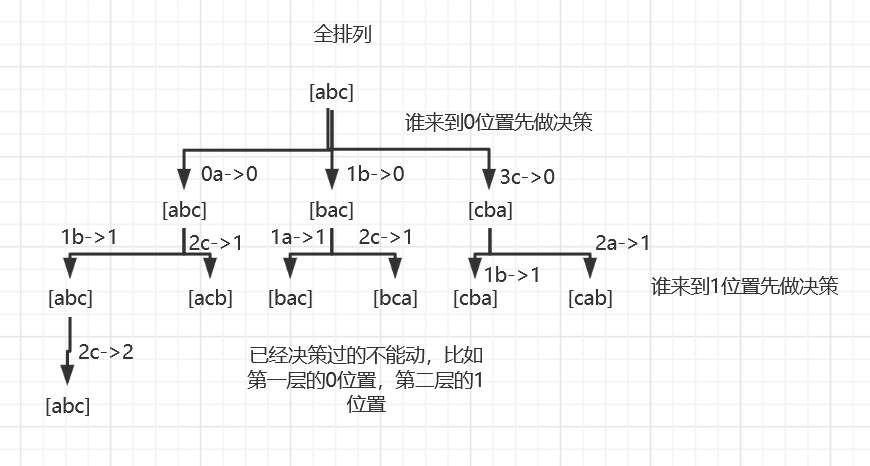
 代码：

         //ch：字符串转成的数组 i：当前位置 res：结果集
         //ch[i..]都有机会来到i位置
         //i终止位置，str当前位置，就是一种结果--->res
        public static void process(char[] ch,int i,ArrayList<String> res){
           if(i == ch.length){
              //将数组转化成一个字符串
              res.add(String.valueOf(ch));
           }
           //i没有到终止位置，i往后所有位置都可以来到i位置
           for(int j = i; i < ch.length; j ++){
                swap(ch,i,j);
                process(ch,i + 1,res);
                swap(ch,i,j);//要恢复现场，相当于一条路走到头最后要返回的走别的路
           }
        }
        
        public static void swap(char[] ch,int a,int b){
             char temp = ch[a];
             ch[a] = ch[b];
             ch[b] = temp;
        }

栗子4

打印一个字符串的全部排列，要求不要出现重复的排列

思路：

    1.可以将全排列都列出来，然后去重，效率低

    2.将结果集做成hashSet，利用hashSet的不允许重复性质

    3.引入分支限界的思路（推荐）

代码：

// str：字符串转成的数组 i：当前位置 res：结果集
    // str[0...i-1]已经做好决定的
    // i终止位置，str当前位置，就是一种结果--->res
    public static void process2(char[] str, int i, ArrayList<String> res) {
        if (i == str.length) {
            res.add(String.valueOf(str));
        }
        //假设26个字母，visited[0]代表a这个字符在当前位置有没有使用过
        boolean[] visited = new boolean[26];
        for (int j = i; j < str.length; j++) {
            //分支限界的思想：如果该字符在当前位置没有出现过才开始走下面的路
            if (!visited[str[j] - 'a']) {//visited[str[j] - 'a':字符转成数，a转成0，b转成1
                
                visited[str[j]- 'a'] = true;
                swap(str, i, j);
                process2(str, i + 1, res);
                swap(str, i, j);
            }
        }

    }

    public static void swap(char[] chs, int i, int j) {
        char tmp = chs[i];
        chs[i] = chs[j];
        chs[j] = tmp;
    }

总结：

    本节主要介绍了暴力递归的基本思路以及举了五个例子来理解递归的套路。我们说过任何一个动态规划问题都是某一个暴力尝试优化后的结果，下一节我们主要介绍几种尝试的模型。