温故10个经典排序算法(Java版)
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。排序算法,就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视,尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。
目录
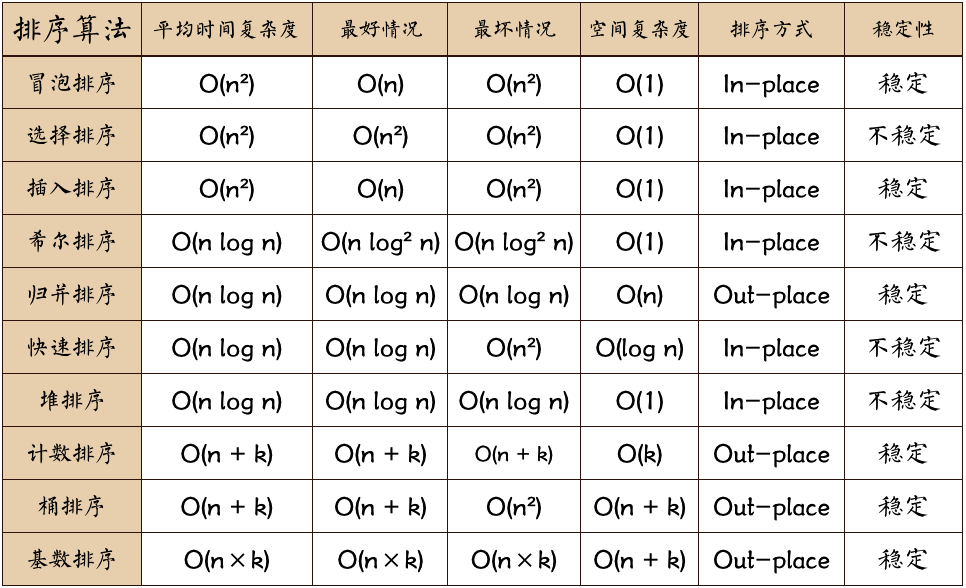
一、冒泡排序
public static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}二、选择排序
public static void selectionSort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
int min = i;
for (int j = i; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
if (min != i) {
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
}三、插入排序
public static void insertSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int current = arr[i + 1];
int index = i;
while (index >= 0 && current < arr[index]) {
arr[index + 1] = arr[index];
index--;
}
arr[index + 1] = current;
}
}四、希尔排序
public static void shellSort(int[] arr) {
int len = arr.length;
int gap = len / 2;
while (gap > 0) {
for (int i = gap; i < len; i++) {
int temp = arr[i];
int index = i - gap;
while (index >= 0 && arr[index] > temp) {
arr[index + gap] = arr[index];
index -= gap;
}
arr[index + gap] = temp;
}
gap /= 2;
}
}五、归并排序
public static void mergeSort(int[] arr) {
//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
int[] temp = new int[arr.length];
sort(arr, 0, arr.length - 1, temp);
}
private static void sort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
int mid = (left + right) / 2;
//左边归并排序,使得左子序列有序
sort(arr, left, mid, temp);
//右边归并排序,使得右子序列有序
sort(arr, mid + 1, right, temp);
//将两个有序子数组合并操作
merge(arr, left, mid, right, temp);
}
}
private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
//左序列指针
int i = left;
//右序列指针
int j = mid + 1;
//临时数组指针
int t = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
//将左边剩余元素填充进temp中
while (i <= mid) {
temp[t++] = arr[i++];
}
//将右序列剩余元素填充进temp中
while (j <= right) {
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while (left <= right) {
arr[left++] = temp[t++];
}
}六、快速排序
public static void quickSort(int[] arr, int low, int hight) {
if (low < hight) {
int privotpos = partition(arr, low, hight);
quickSort(arr, low, privotpos - 1);
quickSort(arr, privotpos + 1, hight);
}
}
public static int partition(int[] arr, int low, int hight) {
int privot = arr[low];
while (low < hight) {
while (low < hight && arr[hight] >= privot) --hight;
arr[low] = arr[hight];
while (low < hight && arr[low] <= privot) ++low;
arr[hight] = arr[low];
}
arr[low] = privot;
return low;
}七、堆排序
public static void heapSort(int[] arr) {
int len = arr.length;
//初始化堆,构造一个最大堆
for (int i = (len / 2 - 1); i >= 0; i--) {
heapAdjust(arr, i, len);
}
//将堆顶的元素和最后一个元素交换,并重新调整堆
for (int i = len - 1; i > 0; i--) {
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
heapAdjust(arr, 0, i);
}
}
public static void heapAdjust(int[] arr, int index, int length) {
//保存当前结点的下标
int max = index;
//当前节点左子节点的下标
int lchild = 2 * index;
//当前节点右子节点的下标
int rchild = 2 * index + 1;
if (length > lchild && arr[max] < arr[lchild]) {
max = lchild;
}
if (length > rchild && arr[max] < arr[rchild]) {
max = rchild;
}
//若此节点比其左右孩子的值小,就将其和最大值交换,并调整堆
if (max != index) {
int temp = arr[index];
arr[index] = arr[max];
arr[max] = temp;
heapAdjust(arr, max, length);
}
}八、计数排序
public static void countingSort(int[] arr) {
if (arr == null || arr.length == 0) return;
int bias, min = arr[0], max = arr[0];
//找出最小值和最大值
for (int i = 0; i < arr.length; i++) {
if (arr[i] < min) {
min = arr[i];
}
if (arr[i] > max) {
max = arr[i];
}
}
//偏差
bias = 0 - min;
//新开辟一个数组
int[] bucket = new int[max - min + 1];
//数据初始化为0
Arrays.fill(bucket, 0);
for (int i = 0; i < arr.length; i++) {
bucket[arr[i] + bias] += 1;
}
int index = 0;
for (int i = 0; i < bucket.length; i++) {
int len = bucket[i];
while (len > 0) {
arr[index++] = i - bias;
len--;
}
}
}九、桶排序
public static void bucketSort(int[] arr) {
if (arr == null || arr.length == 0) return;
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
//桶数
int bucketNum = (max - min) / arr.length + 1;
List<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for (int i = 0; i < bucketNum; i++) {
bucketArr.add(new ArrayList<Integer>());
}
//将每个元素放入桶
for (int i = 0; i < arr.length; i++) {
int num = (arr[i] - min) / (arr.length);
bucketArr.get(num).add(arr[i]);
}
//对每个桶进行排序
for (int i = 0; i < bucketArr.size(); i++) {
Collections.sort(bucketArr.get(i));
}
//将排序结果转为数组
int index = 0;
for (int i = 0; i < bucketArr.size(); i++) {
if (bucketArr.get(i).size() > 0) {
for (int j = 0; j < bucketArr.get(i).size(); j++) {
arr[index++] = bucketArr.get(i).get(j);
}
}
}
}十、基数排序
public static void radixSort(int[] arr) {
if (arr == null || arr.length == 0) return;
// 桶 10个桶 每个桶的最大容量默认为数组长度
int[][] bucket = new int[10][arr.length];
// 每个桶的当前容量
int[] capacity = new int[10];
// 注意:正数负数共用10个桶 不要再重新定义 节约内存 因为每次都有清理空
int negative_number = 0;// 记录负数个数
int positive_number = 0;// 记录正数个数
int[] negative_arr = new int[arr.length];// 存放负数
int[] positive_arr = new int[arr.length];// 存放正数
// 记录正数最大值 和负数最小值 用于记录长度
int max = positive_arr[0];
int min = negative_arr[0];
// 先把原数组分成一个负数数组 和一个正数数组 并找出正数最大值
for (int a = 0; a < arr.length; a++) {
if (arr[a] < 0) {
negative_arr[negative_number] = arr[a];
negative_number += 1;
} else {
positive_arr[positive_number] = arr[a];
positive_number += 1;
}
// 找出正数最大值
if (arr[a] > max) {
max = arr[a];
}
}
// 把负数数组变成正数数组 再找出最大值
for (int r = 0; r < negative_number; r++) {
negative_arr[r] = negative_arr[r] / (-1);
// 此时的负数数组已经是正数
if (negative_arr[r] > min) {
min = negative_arr[r];
}
}
// 先排序正数
for (int b = 0, u = 1; b < positive_number; b++, u *= 10) {
for (int i = 0; i < positive_number; i++) {
int base = positive_arr[i] / u % 10; // 比如基数为 4
// 将基数按照规则放进桶中
bucket[base][capacity[base]] = positive_arr[i]; // 放进第四个桶中 的第一几个当前容量位置
capacity[base]++; // 容量增加
}
// 取出数据
int d = 0;
for (int k = 0; k < capacity.length; k++) {
if (capacity[k] != 0) {
for (int p = 0; p < capacity[k]; p++) {
positive_arr[d] = bucket[k][p];
d++;
}
}
// 注意:清零
capacity[k] = 0;
}
}
// 排序负数数组 正数差不多 注意最后取出数据的时候 才大到小 不再是从小到大
for (int b = 0, u = 1; b < negative_number; b++, u *= 10) {
for (int i = 0; i < negative_number; i++) {
int base = negative_arr[i] / u % 10;
bucket[base][capacity[base]] = negative_arr[i]; // 放进第四个桶中 的第一几个当前容量位置
capacity[base]++;
}
int d = 0;
for (int k = capacity.length - 1; k >= 0; k--) {
if (capacity[k] != 0) {
for (int p = 0; p < capacity[k]; p++) {
negative_arr[d] = bucket[k][p];
d++;
}
}
// 注意:清零
capacity[k] = 0;
}
}
// 把负数数组转化成负数 覆盖给原来的数组(从0开始)
int c = 0;
for (int e = 0; e < negative_number; e++) {
arr[c] = negative_arr[e] / (-1);
c++;
}
// 正数接上原来数组
for (int t = 0; t < positive_number; t++) {
arr[c] = positive_arr[t];
c++;
}
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号