蓝桥杯历年真题JAVA版-2015年蓝桥杯省赛- Java组
第1题——星系炸弹
(1)题目描述
在X星系的广袤空间中漂浮着许多X星人造“炸弹”,用来作为宇宙中的路标。
每个炸弹都可以设定多少天之后爆炸。
比如:阿尔法炸弹2015年1月1日放置,定时为15天,则它在2015年1月16日爆炸。
有一个贝塔炸弹,a年b月c日放置,定时为n天,请你计算它爆炸的准确日期。输入格式:
输入存在多组数据,每组数据输入一行,每一行输入四个正整数a,b,c,n
输入保证日期在1000-01-01到2020-01-01之间,且日期合法。
n不超过1000输出格式:
请填写该日期,格式为 yyyy-mm-dd 即4位年份2位月份2位日期。
比如:2015-02-19
请严格按照格式书写。不能出现其它文字或符号。
输入样例:
2015 1 1 15
2014 11 9 1000输出样例 :
2015-01-16
2017-08-05
(2)解题代码
/**
*
* @param a 年
* @param b 月
* @param c 日
* @param n 天数
*/
public static void func1(int a, int b, int c, int n) {
// 参数校验
if ((a < 1000 || a > 2020) || (b < 0 || b > 12) || (c < 0 || c > 31) || (n < 0 || n > 1000)) {
System.out.println("输入不合法");
return;
}
Calendar calendar = Calendar.getInstance();
calendar.set(a, b - 1, c);
SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd");
// n天后
calendar.add(Calendar.DAY_OF_YEAR, n);
System.out.println(sdf.format(calendar.getTime()));
}
(3)输出结果

第2题——牌型种数
(1)题目描述
小明被劫持到X赌城,被迫与其他3人玩牌。
一副扑克牌(去掉大小王牌,共52张),均匀发给4个人,每个人13张。
这时,小明脑子里突然冒出一个问题:
如果不考虑花色,只考虑点数,也不考虑自己得到的牌的先后顺序
自己手里能拿到的初始牌型组合一共有多少种呢?
(2)解题代码
int sum = 0;
/**
*
* @param pos 牌型1-13
* @param cnt 手里牌的数目
*/
public void func2(int pos, int cnt) {
if (cnt == 13) {
sum++;
return;
}
if (pos == 13) {
return;
}
// 取两者中的小值
int min = Math.min(13 - cnt, 4);
for (int i = 0; i <= min; i++) {
func2(pos + 1, cnt + i);
}
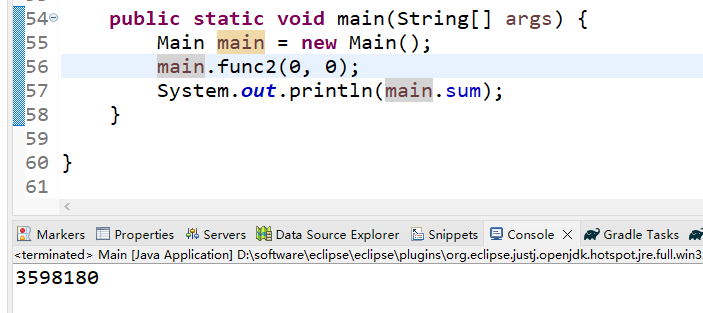
}(3)运行结果
第3题——垒骰子
(1)题目描述
赌圣atm晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。
经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!
我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。
atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模 10^9 + 7 的结果。输入格式:
输入存在多组测试数据,对于每组数据:
第一行两个整数 n m(0<n<10^9,m<=36)
n表示骰子数目
接下来 m 行,每行两个整数 a b ,表示 a 和 b 数字不能紧贴在一起。输出格式:
对于每组测试数据,输出一行,只包含一个数,表示答案模 10^9 + 7 的结果。
输入样例 :
2 11 2
输出样例:
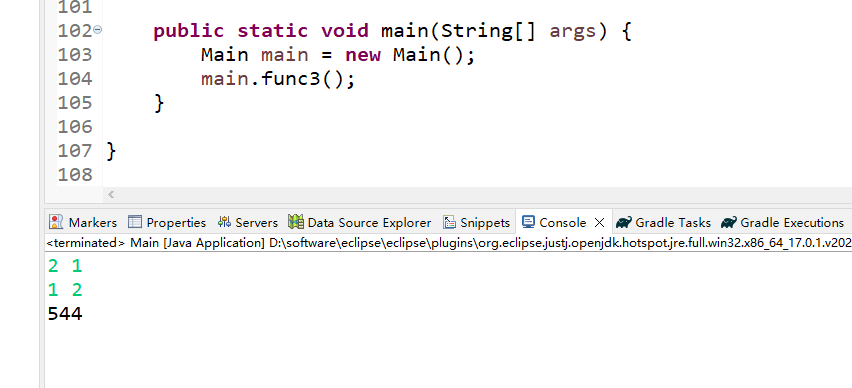
544
(2)解题代码
public static int n, m;
public static int[][] oje = new int[7][7];
public static int count = 0;
public static int[] dui = { 0, 4, 5, 6, 1, 2, 3 };
public static int mode = 1000000007;
public static void dfs(int i, int di) {
if (i == n) {
count++;
if (count > mode)
count -= mode;
} else {
if (di == -1) {
for (int j = 1; j < 7; j++) {
dfs(i + 1, dui[j]);
}
} else {
for (int j = 1; j < 7; j++) {
if (oje[j][di] == 0) {
dfs(i + 1, dui[j]);
}
}
}
}
}
public void func3() {
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
int a, b;
for (int i = 0; i < m; i++) {
a = in.nextInt();
b = in.nextInt();
oje[a][b] = 1;
oje[b][a] = 1;
}
dfs(0, -1);
int ans = 1;
for (int i = 0; i < n; i++) {
ans = (ans * 4) % mode;
}
System.out.println((count * ans) % mode);
in.close();
}(3)运行结果
第4题——灾后重建
(1)题目描述
Pear市一共有N(<=50000)个居民点,居民点之间有M(<=200000)条双向道路相连。
这些居民点两两之间都可以通过双向道路到达。
这种情况一直持续到最近,一次严重的地震毁坏了全部M条道路。
震后,Pear打算修复其中一些道路,修理第i条道路需要Pi的时间。
不过,Pear并不打算让全部的点连通,而是选择一些标号特殊的点让他们连通。
Pear有Q(<=50000)次询问,每次询问,他会选择所有编号在[l,r]之间,并且 编号 mod K = C 的点,修理一些路使得它们连通。
由于所有道路的修理可以同时开工,所以完成修理的时间取决于花费时间最长的一条路,即涉及到的道路中Pi的最大值。
你能帮助Pear计算出每次询问时需要花费的最少时间么?
这里询问是独立的,也就是上一个询问里的修理计划并没有付诸行动。
输入格式:第一行三个正整数N、M、Q,含义如题面所述。
接下来M行,每行三个正整数Xi、Yi、Pi,表示一条连接Xi和Yi的双向道路,修复需要Pi的时间。
可能有自环,可能有重边。1<=Pi<=1000000。
接下来Q行,每行四个正整数Li、Ri、Ki、Ci,表示这次询问的点是[Li,Ri]区间中所有编号Mod Ki=Ci的点。
保证参与询问的点至少有两个。输出格式:
输出Q行,每行一个正整数表示对应询问的答案。
输入样例:
7 10 4
1 3 10
2 6 9
4 1 5
3 7 4
3 6 9
1 5 8
2 7 4
3 2 10
1 7 6
7 6 9
1 7 1 0
1 7 3 1
2 5 1 0
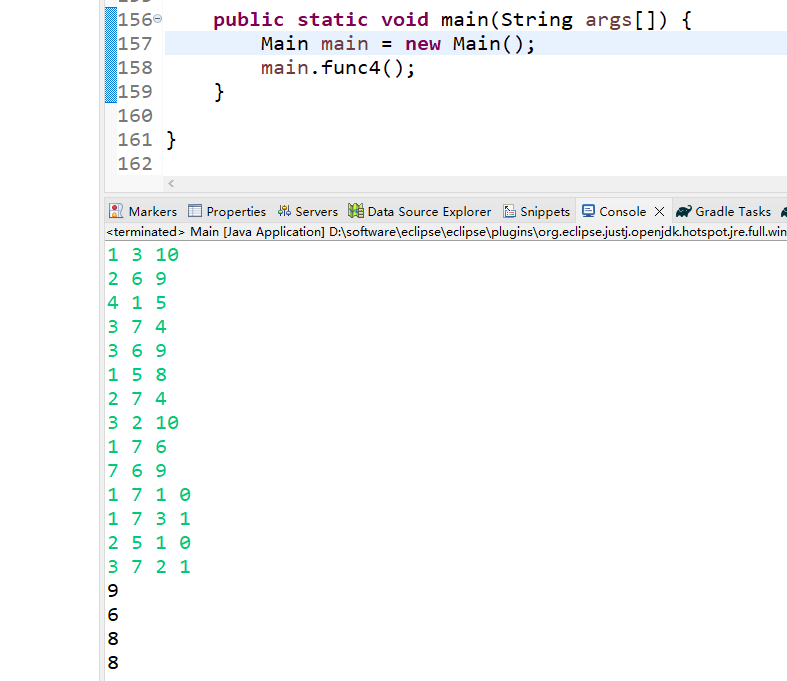
3 7 2 1输出样例:
9
6
8
8
(2)解题代码
public static int N, M, Q;
public static Edge[] edges;
public static UnionFind uf;
public static ArrayList<Integer> costs = new ArrayList<Integer>();
/**
* 逐步加入边到最小生成树中,若加入该边后使得[l,r]中余mod等于c的点连通,则输出最后加入的边的cost
*
* @param l 左边界
* @param r 右边界
* @param mod 模
* @param c 余数
*/
public static void buildMst(int l, int r, int mod, int c) {
for (int i = 0; i < uf.ufNodes.length; i++) {
uf.ufNodes[i].parent = null;
}
for (int i = 0; i < M; i++) {
Edge edge = edges[i];
int from = edge.from;
int to = edge.to;
int cost = edge.cost;
// 如果该边加入不会构成环,则将其加入最小生成树
if (uf.find(from) == uf.find(to)) {
continue;
} else {
uf.merge(from, to);
}
// 判断要关注的所有点是否连通
boolean isOk = true;
UnionFind.UFNode parent = null;
for (int j = l; j <= r; j++) {
if (j % mod == c) {
if (parent == null) {
parent = uf.find(j); // 第一个关注点的老大
} else {
if (parent != uf.find(j)) { // 没有连通
isOk = false;
break;
}
}
}
}
// 如果isOk为true,说明最后加的一条边即为使得要关注的点连通的边,输出cost则为最大花费
if (isOk) {
costs.add(Integer.valueOf(cost));
break;
}
}
}
public static class Edge implements Comparable<Edge> {
public int from; // 边的起点
public int to; // 边的终点
public int cost; // 代价
public Edge(int from, int to, int cost) {
super();
this.from = from;
this.to = to;
this.cost = cost;
}
public Edge() {
}
@Override
public int compareTo(Edge o) {
return cost > o.cost ? 1 : (cost == o.cost) ? 0 : -1;
}
}
// 并查集
public static class UnionFind {
UFNode[] ufNodes;
int count;
public static class UFNode {
UFNode parent;
}
public UnionFind(int count) {
ufNodes = new UFNode[count];
for (int i = 0; i < ufNodes.length; i++) {
ufNodes[i] = new UFNode();
}
this.count = count;
}
// 查找并压缩查找路径
UFNode find(int i) {
UFNode node = ufNodes[i];
// 本身就是树根
if (node == null) {
return node;
}
// set存储不是根节点的UFNode,之后用来压缩路径
Set<UFNode> set = new HashSet<UFNode>();
// 寻找树根
while (node.parent != null) {
set.add(node);
node = node.parent;
}
// 压缩路径,让某个并查集的所有元素的parent为该集合的老大
for (UFNode ufNode : set) {
ufNode.parent = node;
}
return node;
}
// 合并两个并查集
void merge(int a, int b) {
find(b).parent = find(a);
}
}
public void func4() {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
M = sc.nextInt();
Q = sc.nextInt();
edges = new Edge[M];
uf = new UnionFind(N + 1);
for (int i = 0; i < edges.length; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int cost = sc.nextInt();
edges[i] = new Edge(a, b, cost);
}
Arrays.sort(edges); // 将边集排序
for (int i = 0; i < Q; i++) {
int l = sc.nextInt();
int r = sc.nextInt();
int mod = sc.nextInt();
int c = sc.nextInt();
buildMst(l, r, mod, c);
}
for (Integer i : costs) {
System.out.println(i);
}
sc.close();
}(3)运行结果
第5题——加法边乘法
(1)题目描述
我们都知道:1+2+3+ ... + 49 = 1225
现在要求你把其中两个不相邻的加号变成乘号,使得结果为2015
比如:
1+2+3+...+10*11+12+...+27*28+29+...+49 = 2015 就是符合要求的答案。
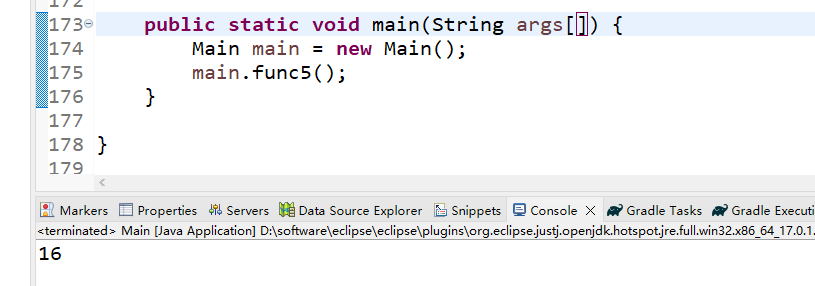
请你寻找另外一个可能的答案,并把位置靠前的那个乘号左边的数字提交。
(对于示例,就是提交10)。输出格式:注意:需要你提交的是一个整数,不要填写任何多余的内容。
(2)解题代码
public void func5() {
int a, b, c, d;
for (int i = 1; i <= 49; i++) {
a = i;
b = i + 1;
for (int j = i + 2; j <= 49; j++) {
c = j;
d = j + 1;
if (a * b + c * d - (a + b) - (c + d) == 790 && a != 10) {
System.out.println(a);
break;
}
}
}
}(3)运行结果
第6题——移动距离
(1)题目描述
X星球居民小区的楼房全是一样的,并且按矩阵样式排列。
其楼房的编号为1,2,3... 当排满一行时,从下一行相邻的楼往反方向排号。
比如:当小区排号宽度为6时,开始情形如下:1 2 3 4 5 6
12 11 10 9 8 7
13 14 15 .....我们的问题是:已知了两个楼号m和n,需要求出它们之间的最短移动距离
(不能斜线方向移动)
输入格式:输入存在多组测试数据
输入为3个整数w m n,空格分开,都在1到10000范围内
w为排号宽度,m,n为待计算的楼号。输出格式:
要求输出一个整数,表示m n 两楼间最短移动距离。
输入样例:
6 8 2
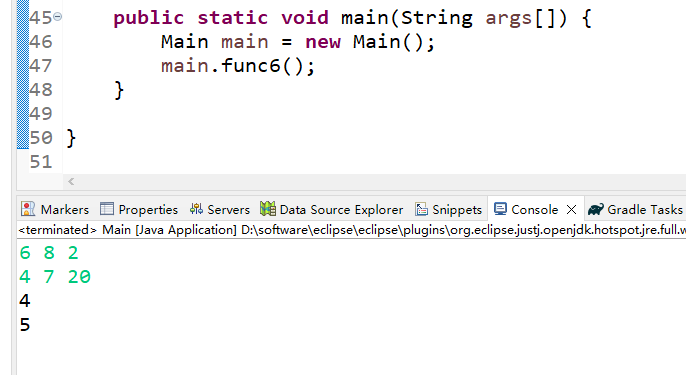
4 7 20输出样例:
45
(2)解题代码
public int[] zb(int m, int w) {
int sz[] = new int[2];
int x = 0, y = 0;
int a = 0;
if (m % w == 0) {
a = m / w;
} else {
a = m / w + 1;
}
if (a % 2 == 0) {
x = w + 1 - m % w;
y = a;
} else {
x = m % w;
y = a;
}
sz[0] = x;
sz[1] = y;
return sz;
}
public void func6() {
Scanner in = new Scanner(System.in);
List<Integer> result = new ArrayList<>();
for (int i = 0; i < 2; i++) {
int w = in.nextInt();
int m = in.nextInt();
int n = in.nextInt();
int distance = Math.abs((zb(m, w)[1] - zb(n, w)[1])) + Math.abs((zb(m, w)[0] - zb(n, w)[0]));
result.add(distance);
}
result.forEach(System.out::println);
in.close();
}(3)运行结果
第7题——饮料换购
(1)题目描述
乐羊羊饮料厂正在举办一次促销优惠活动。
乐羊羊C型饮料,凭3个瓶盖可以再换一瓶C型饮料,并且可以一直循环下去(但不允许暂借或赊账)。
请你计算一下,如果小明不浪费瓶盖,尽量地参加活动。
那么,对于他初始买入的n瓶饮料,最后他一共能喝到多少瓶饮料。输入格式:
输入存在多组测试数据
每组测试数据输入一行包含一个正整数n(1<=n<=10000)输出格式:
对于每组数据输出一行,包含一个整数,表示实际得到的饮料数
输入样例 :
100
101
输出样例 :
149
151
(2)解题代码
public void func7() {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int a = n;
int num = 0;
while (true) {
num += a / 3;
a = a / 3 + a % 3;
if (a < 3) {
break;
}
}
System.out.println(num + n);
in.close();
}(3)运行结果


第8题——奇妙的数字
(1)题目描述
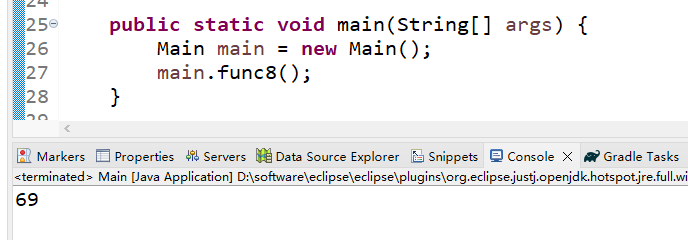
小明发现了一个奇妙的数字。它的平方和立方正好把0~9的10个数字每个用且只用了一次。你能猜出这个数字是多少吗?
(2)解题代码
public static int ans1, ans2;
public void func8() {
for (int i = 1; i < 100; i++) {
ans1 = i * i;
ans2 = ans1 * i;
String str3 = ans1 + "" + ans2 + "";
char arr[] = str3.toCharArray();
Arrays.sort(arr);
String str = new String(arr);
// 字符串的比较用equals不用==
if (str.equals("0123456789")) {
System.out.println(i);
break;
}
}
}(3)运行结果
第9题——生命之树
(1)题目描述
在X森林里,上帝创建了生命之树。
他给每棵树的每个节点(叶子也称为一个节点)上,都标了一个整数,代表这个点的和谐值。
上帝要在这棵树内选出一个非空节点集S,使得对于S中的任意两个点a,b,都存在一个点列 {a, v1, v2, ..., vk, b}
使得这个点列中的每个点都是S里面的元素,且序列中相邻两个点间有一条边相连。
在这个前提下,上帝要使得S中的点所对应的整数的和尽量大。
这个最大的和就是上帝给生命之树的评分。
经过atm的努力,他已经知道了上帝给每棵树上每个节点上的整数。
但是由于 atm 不擅长计算,他不知道怎样有效的求评分。
他需要你为他写一个程序来计算一棵树的分数。
输入格式:第一行一个整数 n 表示这棵树有 n 个节点。(0<n<=10^5)
第二行 n 个整数,依次表示每个节点的评分。(每个节点的评分不超过10^6)
接下来 n-1 行,每行 2 个整数 u, v,表示存在一条 u 到 v 的边。
由于这是一棵树,所以是不存在环的。输出格式:
输出一行一个数,表示上帝给这棵树的分数。
输入样例:
5
1 -2 -3 4 5
4 2
3 1
1 2
2 5输出样例:
8
(2)解题代码
public static int n;// 节点数
public static int[] v;// 节点集合
public static int[][] arr;// 节点边表示集合
public static boolean[] vis;
public static int max = 0;// 节点连接的最大值
public static void dfs(int m) {
if (m == n) {
return;
}
for (int i = 1; i <= n; i++) {
if (vis[i] == false && arr[m][i] != 0) {// vis[i] == false是限界函数,arr[m][i] != 0是约束函数
vis[i] = true;
if (v[m] < (v[m] + v[i])) {
v[m] = v[m] + v[i];
}
max = Math.max(max, v[m]);
dfs(i);
}
}
}
public void func9() {
Scanner in = new Scanner(System.in);
n = in.nextInt();
v = new int[n + 1];
arr = new int[n + 1][n + 1];
vis = new boolean[n + 1];
for (int i = 1; i <= n; i++) {
v[i] = in.nextInt();
}
for (int i = 1; i < n; i++) {
int a = in.nextInt();
int b = in.nextInt();
arr[a][b] = 1;
arr[b][a] = 1;
}
dfs(1);
System.out.println(max);
in.close();
}
(3)运行结果
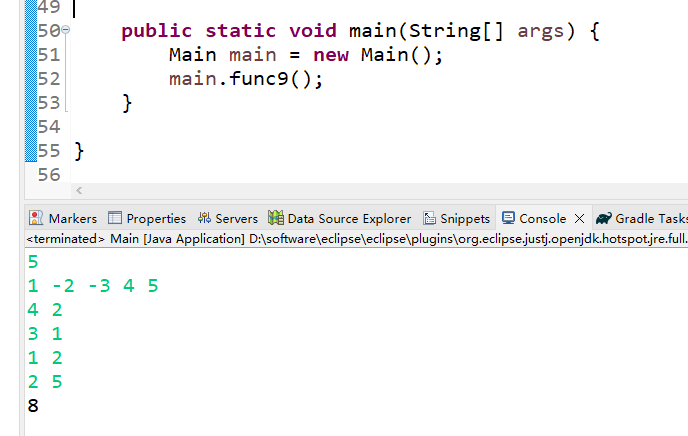
第10题——三羊献瑞
(1)题目描述
观察下面的加法算式:
其中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请你填写“三羊献瑞”所代表的4位数字(答案唯一),不要填写任何多余内容。
(2)解题代码
public void f(int[] a, int[] b, int i) {
// 结束条件
if (i == a.length) {
int x = a[0] * 1000 + a[1] * 100 + a[2] * 10 + a[3];
int y = a[4] * 1000 + a[5] * 100 + a[6] * 10 + a[1];
int z = a[4] * 10000 + a[5] * 1000 + a[2] * 100 + a[1] * 10 + a[7];
if (x + y == z) {
if (y / 1000 > 0)
System.out.println(y);
}
return;
}
for (int j = 0; j < b.length; j++) {
if (b[j] != -1) {
a[i] = b[j]; // 取数放进容器a里
b[j] = -1; // 已使用,标记-1
f(a, b, i + 1);
b[j] = a[i]; // 调用结束了,把容器a里的数还回去
}
}
}
(3)运行结果
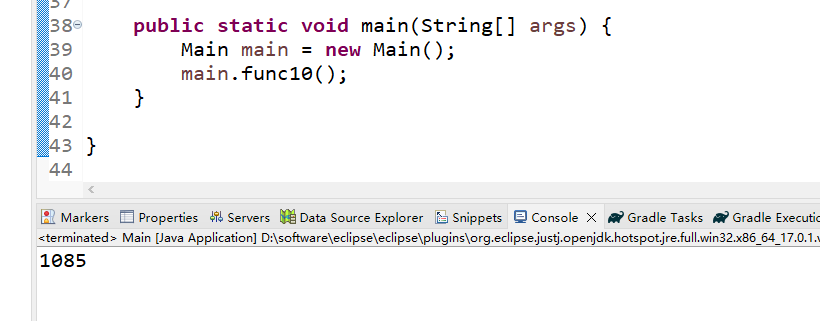
第11题——打印大X
(1)题目描述
小明希望用星号拼凑,打印出一个大X,他要求能够控制笔画的宽度和整个字的高度。
为了便于比对空格,所有的空白位置都以句点符来代替。
要求输入两个整数m n,表示笔的宽度,X的高度。
输入格式:
输入存在多组数据
每组测试数据输入一行,包含两个整数,用空格分开
(0<m<n, 3<n<1000, 保证n是奇数)输出格式:
要求输出一个大X
输入样例:
3 9
4 21输出样例:
***.....***
.***...***.
..***.***..
...*****...
....***....
...*****...
..***.***..
.***...***.
***.....***
****................****
.****..............****.
..****............****..
...****..........****...
....****........****....
.....****......****.....
......****....****......
.......****..****.......
........********........
.........******.........
..........****..........
.........******.........
........********........
.......****..****.......
......****....****......
.....****......****.....
....****........****....
...****..........****...
..****............****..
.****..............****.
****................****
(2)解题代码
public void func11(int m, int n) {
// 列=n+m-1
int cols = n + m - 1;
char a[][] = new char[n][cols];
if (n > m && m > 0 && n > 3 && n < 1000) {
int i, j;
// 将图形全部初始化为. ,然后再找*的位置
for (i = 0; i < n; i++)
for (j = 0; j < cols; j++)
a[i][j] = '.';
for (i = 0; i < n; i++) {
// 主对角线
for (j = i; j < i + m; j++)
a[i][j] = '*';
// 副对角线
for (j = cols - 1 - i; j >= cols - m - i; j--)
a[i][j] = '*';
}
// 打印图形
for (i = 0; i < n; i++) {
for (j = 0; j < cols; j++)
System.out.print(a[i][j]);
System.out.println();
}
}
}
(3)运行结果
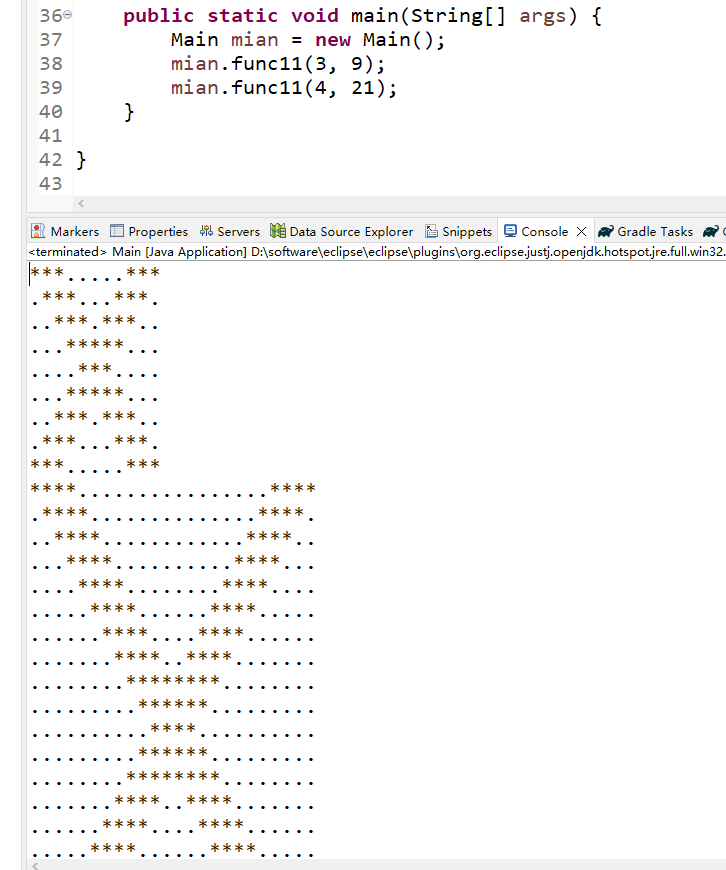



 浙公网安备 33010602011771号
浙公网安备 33010602011771号