组合数学

基本概念

排列

排列是有序的。

不可重复排列数：从 \(n\) 个数中不重复的取出 \(r\) 个，排列数 \(P_{n}^{r} = n(n - 1)(n - 2) \dots (n - r + 1) = \frac{n!}{(n - r)!}\)
可重复排列数：从 \(n\) 个不同的物品中可重复的取出 \(r\) 个，排列数为 \(n ^ r\)。
圆排列（循环排列，环排列）的排列数：从 \(n\) 个元素中选 \(r\) 个的圆排列的排列数为 \(\frac{P_n^r}{r} = \frac{n!}{r(n - r)!}\)。

组合

组合是无序的。组合数 \(C_n^r = \frac{P_n^r}{r!} = \frac{n!}{r!(n - r)!}\)，表示从 \(n\) 个元素中选择 \(r\) 个的方案数。

组合数有三个重要性质：

\(C_n^r = C_n^{n - r}\)。从 \(n\) 个元素中拿出 \(r\) 个等价于丢掉 \(n - r\) 个。
\(C_n^r = C_{n - 1}^{r} + C_{n - 1}^{r - 1}\)，称为帕斯卡公式。可以用 dp 思路证明：第 \(n\) 个元素取还是不取，如果取，就是需要从 \(n - 1\) 个元素中选择 \(r - 1\) 个，如果不去，就是从 \(n - 1\) 个元素中取 \(r\) 个。
\(C_n^0 + C_n^1 + \dots + C_n^n = 2 ^ n\)。

多重集的排列和组合

如果 \(S\) 中的元素可以相同，那么称 \(S\) 为多重集。

无限多重集的排列：令 \(S\) 是一个多重集，它有 \(k\) 个元素，每个元素都有无限个，那么 \(S\) 的 \(r\) 排列的个数为 \(k ^ r\)。
有限多重集的排列：令 \(S\) 是一个多重集，它有 \(k\) 个元素，每个元素的重数分别为 \(n_1, n_2, \dots, n_k\)，\(S\) 的大小为 \(n = n_1 + n_2 + \dots n_k\)，则 \(S\) 的 \(n\) 排列的个数为 \(\frac{n!}{n_1!n_2! \dots n_k!}\)。
有限多重集的组合：令 \(S\) 是一个多重集，它有 \(k\) 个元素，每个元素的重数分别为 \(n_1, n_2, \dots, n_k\)，\(S\) 的大小为 \(n = n_1 + n_2 + \dots n_k\)，则 \(S\) 的 \(r\) 组合的个数为 \(C_{r + k - 1} ^ r = C_{r + k - 1} ^ {k - 1}\)。

鸽巢原理

鸽巢原理也称为抽屉原理。

简单形式

将 \(n + 1\) 个物品分成 \(n\) 组，至少有一组有两个（及以上）的物品。

可以通过反证法证明：如果每组都只有一个，那么最多就只会有 \(n\) 个物品，但是这里有 \(n + 1\) 个物品。

推广

将 \(n\) 个物体，划分为 \(k\) 组，那么至少存在一个分组，含有大于或等于 \(\left \lceil \dfrac{n}{k} \right \rceil\) 个物品。

二项式定理和杨辉三角

组合公式 \(C_n^r = \frac{n!}{r!(n - r)!}\)，把 \(C_n^r\) 称为二项式系数。

二项式系数 \(C_n^r\) 就是 \((1 + x) ^ n\) 展开后第 \(r\) 项的系数。

所以有

\[(1 + x) ^ n = \sum\limits_{r = 0} ^ n C_n^r x^r \]

推导得

\[(a + b) ^ n = \sum\limits_{r = 0} ^ n C_n^r b^r a^{n - r} \]

这个公式称为二项式定理。

所以有两种方法计算二项式系数：

用帕斯卡公式：\(C_n^r = C_{n - 1} ^ r + C_{n - 1} ^ {r - 1}\)，时间复杂度为 \(O(n ^ 2)\)。

for (int i = 0; i < N; i++) {
  c[i][0] = 1;
}
for (int i = 1; i < N; i++) {
  c[i][i] = 1;
  for (int j = 1; j < i; j++) {
    c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % k;
  }
}

用逆直接计算，预处理出单个元素的逆，阶乘取模后的结果和阶乘的逆元，时间复杂度为 \(O(n)\)。

void P() {
  inv[1] = 1;
  for (int i = 2; i <= MAXV; i++) {
    inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;
  }
  fact[0] = factinv[0] = 1;
  for (int i = 1; i <= MAXV; i++) {
    fact[i] = 1ll * fact[i - 1] * i % mod;
    factinv[i] = 1ll * factinv[i - 1] * inv[i] % mod;
  }
}

long long C(int a, int b) {
  return 1ll * fact[a] * factinv[b] % mod * factinv[a - b] % mod;
}

卢卡斯定理

卢卡斯定理用于计算组合数取模，即求 \(C_n^r \bmod m\)，其中 \(m\) 为质数。

对于非负整数 \(n, r\) 和质数 \(m\)，有

\[C_n^r \equiv C_{n \bmod m}^{r \bmod m} \ \cdot \ C_{n / m}^{r / m} \pmod m \]

公式分为两部分：

\(C_{n \bmod m}^{r \bmod m} \pmod m\) 用逆直接计算二项式公式即可。
\(C_{n / m}^{r / m}\) 继续用卢卡斯定理展开，递归实现。

void F() {
  inv[1] = 1;
  for (int i = 2; i <= MAXV; i++) {
    inv[i] = 1ll * (p - p / i) * inv[p % i] % p;
  }
  fact[0] = factinv[0] = 1;
  for (int i = 1; i <= MAXV; i++) {
    fact[i] = 1ll * fact[i - 1] * i % p;
    factinv[i] = 1ll * factinv[i - 1] * inv[i] % p;
  }
}

ll C(int a, int b) {
  return 1ll * fact[a] * factinv[b] % p * factinv[a - b] % p;
}

ll Lucas(int a, int b) {
  return !b ? 1 : Lucas(a / p, b / p) * C(a % p, b % p) % p;
}

时间复杂度为 \(O(n)\)，主要在于预处理上。

容斥原理

容斥原理是一个基本的计数原理：不能重复也不能遗漏。

在计数时，有时情况比较多，互相有重叠，可以先算出不考虑重叠的部分，再减去重叠的部分。

容斥原理的简单形式

设 \(A\) 和 \(B\) 是分别具有性质 \(P_1\) 和 \(P_2\) 的有限集，则有

容斥原理的定义

容斥原理：集合 \(S\) 的子集 \(A_1\) 有性质 \(P_1\)，\(A_2\) 有性质 \(P_2\)，\(\dots\)，\(A_n\) 有性质 \(P_n\)，有以下两种定义。

集合 \(S\) 中不具有性质 \(P_1, P_2, \dots, P_n\) 的对象个数为

\[\left| \overline{A_1} \cap \overline{A_2} \cap \dots \cap \overline{A_n} \right| = \left| S \right| - \sum \left| A_i \right| + \sum \left| \overline{A_i} \cap \overline{A_j} \right| - \sum \left| \overline{A_i} \cap \overline{A_j} \cap \overline{A_k} \right| + \dots + (-1) ^ n \left| \overline{A_1} \cap \overline{A_2} \cap \dots \cap \overline{A_n} \right| \]

集合 \(S\) 中至少具有性质 \(P_1, P_2, \dots, P_n\) 之一的对象的个数为

\[\left| A_1 \cup A_2 \cup \dots \cup A_n \right| = \sum \left| A_i \right| - \sum \left| A_i \cap A_j \right| + \sum \left| A_i \cap A_j \cap A_k \right| + \dots + (-1) ^ {n + 1} \left| A_1 \cap A_2 \cap \dots \cap A_n \right| \]

Catalan 数（卡特兰数）

Catalan 数的计算公式涉及组合计数，它是很多组合问题的数学模型，是一个很常见的数列。

定义

Catalan 数是一个数列，它的一种定义是

\[C_n = \frac{1}{n + 1} \dbinom{2n}{n}, n = 0, 1, 2, \dots \]

Catalan 数有三种计算公式：

\(C_n = \frac{1}{n + 1} \dbinom{2n}{n} = \dbinom{2n}{n} - \dbinom{2n}{n + 1} = \dbinom{2n}{n} - \dbinom{2n}{n - 1}\)
递推，\(C_n = C_0 C_{n - 1} + C_1 C_{n - 2} \dots + C_{n - 1} C_0 = \sum C_k C_{n - k}, C_0 = 1\)
\(C_n = \frac{4n - 2}{n + 1} C_{n - 1}, C_0 = 1\)

由公式 3 可知，当 \(n\) 很大时，\(C_n / C_{n - 1} \approx 4\)。所以 Catalan 数的增长是 \(O(4 ^ n)\) 的，增长极快。

应用场合：

公式 2 的应用场合：\(n\) 较小，复杂度为 \(O(n ^ 2)\)。
公式 1 和公式 3 的应用场合：\(n\) 非常大，不能直接输出 Catalan 数，需要取模。但是，由于公式 1 和公式 3 有大数除法，需要转换成逆元，再取模。先预处理 \(n\) 的阶乘，再用公式计算。

应用

棋盘问题

一个 \(n \times n\) 的棋盘，从左下角走到右上角，一直在对角线的右下方走，不穿过主对角线，有多少种走法？

我们定义向上为 \(0\)，向右为 \(1\)。

满足要求的路线其实就是在任意时刻 \(k\) 1 的个数大于等于 0 的个数。

设总共有 \(X\) 条路线，分成 \(2\) 部分：对角线下面的 \(A\)，对角线上面或者穿过对角线的 \(Y\)。所以 \(A = X - Y\) 就是答案。

总路线 \(X = \dbinom{2n}{n}\)，它的意思就是，在 \(2n\) 步中要挑选出 \(n\) 步向右走，其他的向上走。

我们将第一次碰到 \(y = x + 1\) 的位置 \(d\) 记录下来，然后把 \(d\) 之后的路径沿着 \(y = x + 1\) 对称过去，就像这样。

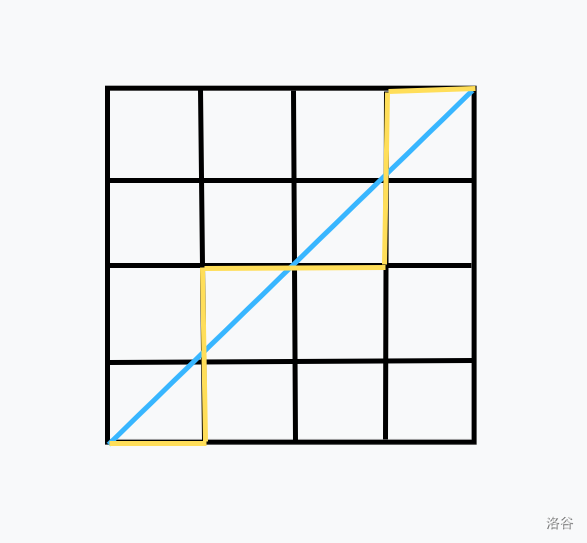
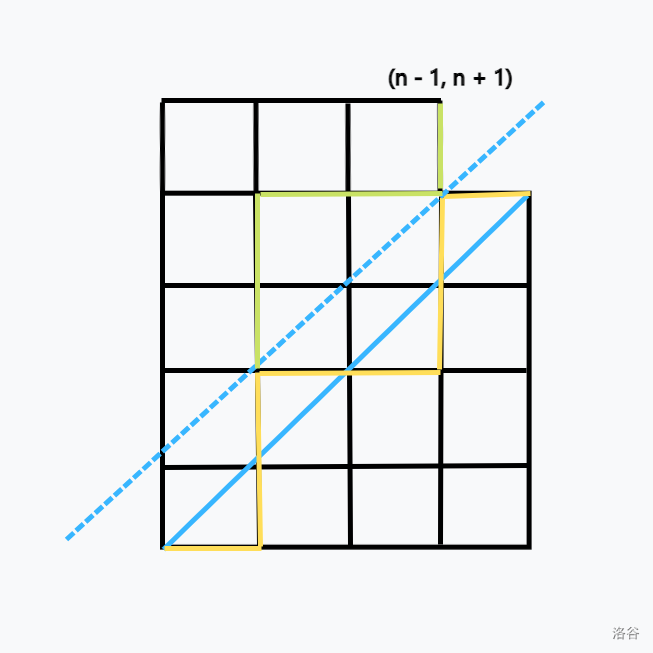
这时，有 \(n + 1\) 个 0，\(n - 1\) 个 1，所以，有 \(Y = \dbinom{2n}{n - 1}\)。可得 \(A = X - Y = \dbinom{2n}{n} - \dbinom{2n}{n - 1}\)。

括号问题

有 \(n\) 个左括号和 \(n\) 个右括号，请问可以组成多少种合法的字符串？

显然，对于前 \(k\) 个字符，左括号的数量必须大于或等于右括号的数量.

定义左括号为 \(0\)，右括号为 \(1\)，模型就变得和棋盘问题是一样的了。

出栈序列问题

给定一个以字符串形式表示的入栈序列，问一共有多少种可能的出栈顺序？

可以发现，合法的序列是对于出栈序列中的每个数字，在它后面的、比它小的所有数字，一定是按递减顺序排列的。

所以，我们定义进栈操作为 \(0\)，出栈操作为 \(1\)。\(n\) 个数的所有状态对应 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) 组成的序列。出栈序列，即要求入栈的操作数大于等于出栈的操作数。也就是说，对于任意前 \(k\) 个序列，\(0\) 的数量大于等于 \(1\) 的数量，就是 Catalan 数。

其实括号问题和出栈序列问题本质上是一样的，括号问题可以用栈模拟。

二叉树问题

\(n\) 个结点构成二叉树，共有多少种情况？

这个问题符合公式 2 的模型，即

\[C_n = C_0 C_{n - 1} + C_1 C_{n - 2} + \dots + C_{n - 1} C_0 = \sum C_k C_{n - k}, C_0 = 1 \]

其含义如下：

\(C_0 C_{n - 1}\)：右子树有 \(0\) 个结点，左子树有 \(n - 1\) 个结点。

\(C_1 C_{n - 2}\)：右子树有 \(1\) 个结点，左子树有 \(n - 2\) 个结点。

\(\dots\)

\(C_{n - 1} C_0\)：右子树有 \(n - 1\) 个结点，左子树有 \(0\) 个结点。

三角剖分问题

有 \(n + 1\) 条边的凸多边形区域，在内部插入不相交的对角线，把凸多边形划分为多个三角形，有多少种方法？

答案是第 \(n - 1\) 个 Catalan 数。

posted @ 2023-10-01 18:53 Yan719 阅读(131) 评论(1) 收藏举报

刷新页面返回顶部

Loading

cn 的小站