Loading

动态规划（dp）

动态规划

简称 dp（dynamic programming），动规

通常来说，最优化问题有分组（阶段）性质，对于每个分组（阶段）的所有状态，只保留它的最优状态。

而动态规划就是按照拓扑序求解每个分组（阶段）的最优状态。

当状态转移满足无后效性（状态转移图存在拓扑序）和最优子结构性质（在拓扑序中靠后的最优状态由靠前的最优状态转移而来）时，可以用动态规划求解。

搜索，递推，动态规划

  1. 状态，转移，剪枝

  2. 初始状态

  3. 状态图遍历（floodfill）

  4. 拓扑序

  5. 收集型，扩散型转移

  6. 递推方程

  7. 记忆化搜索

  8. 分组（阶段）

  9. 最优子结构性质

  10. 状态转移方程

  • 搜索：1，2，3

  • 递推：1，2，3，4，5，6，7

  • 动态规划：1，2，3，4，5，6，7，8，9，10

记忆化搜索

洛谷 P1164

题意

有 \(n\) 件物品，第 \(i\) 件价格为 \(a_i\)，现在你手上有 \(m\) 元，请问有多少种方法可以刚好花完 \(m\) 元。

\(n \le 100, a_i \le 1000, m \le 10000\)

思路

我们首先可以想到暴力，也就是搜索。

考虑对于每一件物品，买还是不买，时间复杂度为 \(O(2 ^ n)\)。

void dfs(int t, int c) {
  if (c < 0) return ;
  if (t == n + 1) {
    ans += !c;
    return ;
  }
  dfs(t + 1, c), dfs(t + 1, c - a[t]);
}

但是是肯定会超时的，因为，有时候，我们会遍历到同一个状态很多遍，很明显，在这里，状态是 \((t, c)\)，\(t\) 代表当前枚举到了第 \(t\) 件物品，\(c\) 表示还剩 \(c\) 元。

所以，我们用一个数组来记录每一个状态所对应的答案，如果当前状态被求解过了，就直接返回答案即可。

int dfs(int t, int c) {
  if (c > m) return 0;
  if (t == n + 1) { 
    return f[t][c] = c == m;
  }
  if (f[t][c] != -1) return f[t][c];  // 当前状态被求解过
  return f[t][c] = dfs(t + 1, c) + dfs(t + 1, c + a[t]);
}

背包

01 背包

我们还是看到上面那道题。

洛谷 P1164

题意

有 \(n\) 件物品，第 \(i\) 件价格为 \(a_i\)，现在你手上有 \(m\) 元，请问有多少种方法可以刚好花完 \(m\) 元。

\(n \le 100, a_i \le 1000, m \le 10000\)

上面，我们的记忆化搜索的代码中有一个数组 \(f_{i, j}\)，表示前 \(i\) 种物品花了 \(j\) 元的方案数。

通过搜索，我们可以看出转移 \(f_{i, j} = f_{i - 1, j} + f_{i - 1, j - a_i} \ (j \ge a_i)\)。

所以，可以直接写循环转移。

f[0][0] = 1;
for (int i = 1; i <= n; i++) {
  for (int j = 0; j <= m; j++) {
    f[i][j] = f[i - 1][j];
    if (j >= a[i]) f[i][j] += f[i - 1][j - a[i]];
  }
}

时间复杂度为 \(O(n \times m)\)。

洛谷 P1048

题意

有 \(m\) 株草药，第 \(i\) 株草药的价值为 \(a_i\)，需要用 \(t_i\) 的时间采摘，你有 \(T\) 个单位的时间，请求出最多可以摘到价值为多少的草药。

思路

状态：\((t, ans, i)\)，前 \(i\) 株草药用了 \(t\) 个单位的时间，总价值为 \(ans\)。

转移：\((t, ans, i - 1), (t - t_i, ans + a_i, i - 1) \to (t, ans, i)\)。

分组：\(dp_{i, j}\) 表示采前 \(i\) 种药用了 \(j\) 个单位时间的 最大总价值。

初始：\(dp_{0, 0} = 0\)。

目标：\(dp_{m, T}\)。

转移方程：

  • \(dp_{i, j} = dp_{i - 1, j}\) 并且 \(0 \leq j < t_i\)。

  • \(dp_{i, j} = max(dp_{i - 1, j}, dp_{i - 1, j - t_i} + a_i)\) 并且 \(j \ge t_i\)。

拓扑序：\(i\) 从小到大。

代码

for (int i = 0; i <= T; i++) {
  for (int j = 1; j <= m; j++) {
    dp[i][j] = dp[i][j - 1];
    if (i >= t[j]) {
      dp[i][j] = max(dp[i - t[j]][j - 1] + a[j], dp[i][j]);
    }
  }
}

时间复杂度为 \(O(T \times m)\)。

总结一下就是这样的：

\(n\) 种物品，每件物品重量为 \(a_i\)，背包承重为 \(m\)，每种物品只有一件（方案数，最优化）。

多重背包

洛谷 P1077

题意

你需要摆 \(m\) 盆花，现在有 \(n\) 种花，第 \(i\) 种有 \(a_i\) 盆。请问有多少种摆花方案。

思路

这个题和 01 背包的区别就在于，这个题的每一种花并不是只有一盆，01 背包的每一种物品只有一个。

所以，我们可以在 01 背包的基础上加上一重循环去枚举当前物品选多少个，就是这样的：

状态：\((i, j)\) 前 \(i\) 种花，摆了 \(j\) 盆。

转移：\((i, j) \to (i + 1, j + k)\) 并且 \(0 \leq k \leq a_i\)。

分组：\(dp_{i, j}\) 表示前 \(i\) 种花摆了 \(j\) 盆的方案数。

初始：\(dp_{0, 0} = 1\)。

目标：\(dp_{n, m}\)。

转移方程：\(dp_{i, j} = \sum \limits_{k = 0}^{min(a_i, j)}{dp_{i - 1, j - k}}\)。

拓扑序：\(i\) 从小到大。

代码

dp[0][0] = 1;
for (int i = 0; i <= m; i++) {
  for (int j = 1; j <= n; j++) {
    for (int k = 0; k <= a[j] && k <= i; k++) {
      dp[i][j] = (dp[i][j] + dp[i - k][j - 1]) % MOD;
    }
  }
}

时间复杂度为 \(O(m \times n \times \max\{a_i\})\)。

洛谷 P6567

题意

有 \(n\) 种钱币，第 \(i\) 种钱币的面值为 \(k_i\) 元，有 \(a_i\) 张。

手表店内有 \(m\) 款手表，第 \(i\) 款的价格为 \(t_i\)，由于手表店不能找零，所以，你必须凑出恰好的钱。

请求出对于每一款手表，能不能凑出 \(t_i\) 元。

思路

状态： \((i, j)\) 前 \(i\) 种面值凑 \(j\) 元。

转移：\((i, j) \to (i + 1, j + k_i \cdot l)\) 并且 \(0 \leq l \leq a_i\)。

分组（阶段）： \(dp_{i, j}\) 表示前 \(i\) 种面值是否能构成 \(j\) 元。

初始：\(dp_{0, 0} = 1\)。

目标: \(dp_{n, t_i}\)。

转移方程：\(dp_{i, j} \models dp_{i - 1, j - k_i \cdot l}\) 并且 \(1 \leq i \leq n, 0 \leq j \leq t, 0 \leq l \leq a_i\)。

拓扑序：\(i\) 从小到大。

代码

dp[0][0] = 1;
for (int i = 0; i <= t; i++) {
  for (int j = 1; j <= n; j++) {
    dp[i][j] = 0;
    for (int l = 0; l <= a[j] && l * k[j] <= i && !dp[i][j]; l++) {
      dp[i][j] |= dp[i - l * k[j]][j - 1];
    }
  }
}

单次询问时间复杂度为 \(O(t_i \times n \times \max\{a_j\})\)。

总价一下：\(n\) 种物品，背包容量为 \(m\)，每种物品有数量限制。

完全背包

洛谷 P1474

题意

有 \(n\) 种货币，第 \(i\) 中的面值是 \(a_i\)，每种货币都有无限张，请问有多少种凑出 \(m\) 元的方式。

思路

这种和 01 背包的不同在于每种面值都不止一张，但是处理方式却有些相同。

\(dp_{i, j}\) 表示前 \(i\) 种货币凑出 \(j\) 元的方案数。

那么，就有转移：

\[dp_{i, j} = dp_{i - 1, j} + dp_{i, j - a_i} \]

dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
  for (int j = 0; j <= m; j++) {
    dp[i][j] = dp[i - 1][j];
    if (j >= a[i]) dp[i][j] += dp[i][j - a[i]];
  }
}

当然，我们可以发现，状态 \((i, j)\) 是由 \((i, j - a_i)\) 转移而来的，也就是说，我们的 dp 数组是可以自我滚动的。

所以，我们可以把 dp 数组优化到一维。

dp[0] = 1;
for (int i = 1; i <= n; i++) {
  for (int j = 0; j <= m; j++) {
    if (j >= a[i]) dp[j] += dp[j - a[i]];
  }
}

洛谷P1616

题意

有 \(m\) 种草药，第 \(i\) 种草药的价值是 \(b_i\)，采摘一株需要 \(a_i\) 个单位的时间。我们有 \(t\) 个单位的时间，请问我们最多可以摘到多少价值的草药。

思路

状态：\((i, x)\)，在时间 \(i\) 内，采药价值为 \(x\)。

转移：\((i, x) \to (i + a_j, x + b_j)\)。

分组：\(dp_i\) 表示在时间 \(i\) 内采药价值最大值。

转移方程：\(dp_i = max\{dp_{i - a_j} + b_j\}\) 并且 \(1 \leq j \leq m\)。

初始：\(dp_i = 0\)。

目标：\(dp_t\)。

拓扑序：\(i\) 从小到大。

代码

for (int i = 0; i <= t; i++) {
  for (int j = 1; j <= m; j++) {
    if (i >= a[j]) dp[i] = max(dp[i], dp[i - a[j]] + b[j]);
  }
}

总结一下：\(n\) 种物品，背包容量为 \(m\)，每种物品无限个，在不超过背包容量下，求方案数 / 最优值。

最长上升子序列

状态：\((i, x)\)，子序列末尾下标为 \(i\)，子序列长度为 \(x\)。原来状态为子序列本身，对于末尾下标相同的子序列合并状态。

转移：\((j, x - 1) \to (i, x)\)，\(i > j\) 并且 \(a_i > a_j\)。

初始状态：空序列，即 \((0, 0)\)，其中 \(a_0\) 为极小值，或以每个数 \(a_i\)开头构建上升子序列，即 \((i, 1)\)。

分组（阶段）：对于同一末尾下标 \(i\) 的所有上升子序列来说， \(x\) 越大越好。即分组（阶段）为 \(i\)，最优化属性为 \(x\)，每个分组保留最大的 \(x\)。
因此，将最优化属性当做状态附加属性，即 \(f_i\)，表示以 \(a_i\) 结尾的上升子序列长度最大值。

目标状态：每个 \(f_i\)，目标答案是 \(\max \{f_i\}\) 且 \(1 \leq i \leq n\)。

拓扑序：在状态转移过程中，末尾下标 \(i\) 不断增长，因此拓扑序为 \(i\) 从小到大（即 \(1 \sim n\)）。

最优子结构性质：在拓扑序中，靠后的 \(f_i\) 一定由靠前的 \(f_i\) 转移而来。

因此有状态转移方程：\(f_i = \max \{f_j\} + 1\) 并且 \(1 \leq j \leq i, a_i \gt a_j\)。

#include <iostream>
#include <algorithm>

using namespace std;

const int MAXN = 2010;

int n, a[MAXN] = {-1}, ans;
int dp[MAXN];  // dp[i] 表示以 a[i] 结尾的最长上升子序列的长度

int main() {
  cin >> n;
  for (int i = 1; i <= n; i++) {
    cin >> a[i];
  }
  for (int i = 1; i <= n; i++) {   // 枚举拓扑序（无后效性）
    for (int j = 0; j < i; j++) {  // 转移
      if (a[j] < a[i]) {
        dp[i] = max(dp[i], dp[j] + 1);  // 状态转移方程（最优子结构性质）
        ans = max(ans, dp[i]);
      }
    }
  }
  cout << ans;
  return 0;
}

时间复杂度为 \(O(n ^ 2)\)。

但是如果我们的 \(n\) 非常大，是会超时的。所以，我们需要更好的算法。

我们看到上面的转移：\(f_i = \max \{f_j\} + 1 \ (1 \le j \le i, a_j < a_i)\)。

所以，我们可以考虑将 \(a_i\) 对应的 \(f_i\) 存在一个新的数组 \(p_{a_i}\) 上，也就是说，\(p_i = \max\limits_{1 \le j \le n, a_j = i}\{f_j\}\) 。

那么，\(f_i = \max\limits_{1 \le j < a_i}\{p_j\} + 1\)，由于有修改操作，所以，我们可以用线段树或者是树状数组维护。

int n, a[N], tr[4 * N], ans;

void modify(int i, int l, int r, int p, int x) {
  if (l == r) {
    tr[i] = max(tr[i], x);
    return ;
  }
  int mid = (l + r) >> 1;
  p <= mid ? modify(i * 2, l, mid, p, x) : modify(i * 2 + 1, mid + 1, r, p, x);
  tr[i] = max(tr[i * 2], tr[i * 2 + 1]);
}

int query(int i, int l, int r, int ql, int qr) {
  if (l > qr || r < ql) {
    return 0;
  }
  if (ql <= l && r <= qr) {
    return tr[i];
  }
  int mid = (l + r) >> 1;
  return max(query(i * 2, l, mid, ql, qr), query(i * 2 + 1, mid + 1, r, ql, qr));
}

void Solve() {
  for (int i = 1; i <= n; i++) {
    cin >> a[i];
  }
  fill(tr, tr + 4 * N, 0), ans = 0;
  for (int i = 1; i <= n; i++) {
    int t = query(1, 1, 30000, 1, a[i]);
    ans = max(ans, t + 1);
    modify(1, 1, 30000, a[i], t + 1);
  }
  cout << ans << '\n';
}

最长公共子序列

我们令 \(dp_{i, j}\) 表示枚举到 \(s\) 的第 \(i\) 个字符，\(t\) 的第 \(j\) 个字符的最长公共子序列的长度。

首先，不管 \(s_i\) 是否等于 \(t_j\)，我们都可以不匹配这两个字符，也就是说，\(dp_{i, j} = \max(dp_{i - 1, j}, dp_{i, j - 1})\)。

但是，如果 \(s_i = t_j\)，就说明当前字符是可以匹配上的，那么就有转移：\(dp_{i, j} = \max(dp_{i, j}, dp_{i - 1, j - 1} + 1)\)。

for (int i = 1; i <= n; i++) {
  for (int j = 1; j <= m; j++) {
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
    if (s[i] == t[j]) dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
  }
}

时间复杂度为 \(O(nm)\)。

区间 dp

我们先看这样一道题目：

洛谷 P1775

题意

有 \(n\) 堆石头排成一排，第 \(i\) 堆石子的质量为 \(m_i\)，现在我们要将这 \(n\) 堆石子合并成一堆，每次合并只能合并相邻的两堆，代价为这两堆石子的质量之和。请问最小代价是多少。

思路

不难发现，合并完的石子在原序列上对应的是一个区间，而不是一个子序列，而这个区间合并完之后的质量就是这个区间的石子的质量之和。

所以，我们用 \(dp_{i, j}\) 表示 \(i \sim j\) 这些石子合并成一堆的最小代价。

由于每堆合并完的石子都对应一个区间，而这堆石子本身又是由两堆石子合并而来。也就是说，区间 \([i, j]\) 是由区间 \([i, k], [k + 1, j]\) 合并而来。那么，我们只需要枚举这个 \(k\)，求出最小值即可。

有转移：

\[dp_{i, j} = \min\limits_{i \le k < j}\{dp_{i, k} + dp_{k + 1, j}\} \]

时间复杂度为 \(O(n ^ 3)\)。

代码

cin >> n;
for (int i = 1; i <= n; i++) {
  cin >> m[i];
  s[i] = s[i - 1] + m[i];
  if (i >= 2) dp[i - 1][i] = m[i - 1] + m[i];
}
for (int len = 3; len <= n; len++) {
  for (int i = 1, j = len; j <= n; i++, j++) {
    dp[i][j] = INT_MAX;
    for (int k = i; k < j; k++) {
      dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1]);
    }
  }
}
cout << dp[1][n];

所以，区间 dp 就是将小区间的信息合并到大区间上，区间长度就是拓扑序。

洛谷 P1880

题意

有 \(n\) 堆石头排成一个环，第 \(i\) 堆石子的质量为 \(m_i\)，现在我们要将这 \(n\) 堆石子合并成一堆，每次合并只能合并相邻的两堆，代价为这两堆石子的质量之和。请问最小代价和最大代价分别是多少。

思路

不难发现，这道题和上一题的区别只有一个：这个题的 \(n\) 堆石头组成的是一个环，上一题组成的是一个序列。

那么，我们只需要将环变成链就可以了。

我们可以将原本的环断开，然后复制一份到后面，这样，就相当于 \(2n\) 堆石头合并，但是统计答案只需要统计长度为 \(n\) 的区间就可以了。

时间复杂度为 \(O(n ^ 3)\)。

代码

for (int i = 1; i <= n; i++) cin >> a[i], a[n + i] = a[i];
for (int i = 1; i <= 2 * n; i++) s[i] = s[i - 1] + a[i];
for (int len = 1; len <= n; len++) {
  for (int l = 1, r = len; r <= 2 * n; l++, r++) {
    for (int k = l; k < r; k++) {
      dp[l][r] = max(dp[l][r], dp[l][k] + dp[k + 1][r] + s[r] - s[l - 1]);
    }
    if (len == n) {
      ans1 = max(ans1, dp[l][r]);
      }
    }
}
for (int i = 1; i <= 2 * n; i++) {
  for (int j = 1; j <= 2 * n; j++) {
    dp[i][j] = 1e9;
  }
  dp[i][i] = 0;
}
for (int len = 1; len <= n; len++) {
  for (int l = 1, r = len; r <= 2 * n; l++, r++) {
    for (int k = l; k < r; k++) {
      dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] + s[r] - s[l - 1]);
    }
    if (len == n) {
      ans2 = min(ans2, dp[l][r]);
    }
  }
}
cout << ans2 << '\n' << ans1;

洛谷 P1435

题意

给定一个字符串 \(s\)，请你求出最少要插入多少个字符能使 \(s\) 变为回文串。

思路

要使 \(s\) 变为回文串，就是要使 \(s_1 = s_n,s_2 = s_{n - 1} \dots\)

所以每次只要保证最两边的字符相同即可。

令 \(f(l, r)\) 表示使 \(s_l \sim s_r\) 变成回文串需要插入的最少字符数量。

  • 如果 \(s_l = s_r\)，则只需要考虑 \(s_{l + 1} \sim s_{r - 1}\) 是否为回文串即可。\(f(l, r) = f(l + 1, r - 1)\)。

  • 如果 \(s_l \ne s_r\)，则有两种情况：一种是让下一个回文的字符为 \(s_l\)，另一种则是让下一个回文的字符为 \(s_r\)。\(f(l, r) = \max \{f(l + 1, r), f(l, r - 1)\} + 1\)，自己需要插入一次。

拓扑序是区间长度从小到大，所以先枚举区间长度。

时间复杂度为 \(O(n ^ 2)\)。

代码

for (int i = 0; i < n - 1; i++) {
  dp[i][i + 1] = s[i] != s[i + 1];   // 初始状态
}
for (int l = 3; l <= n; l++) {
  for (int i = 0, j = l - 1; j < n; i++, j++) {  // 转移
    if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1];
    else dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;
  }
}

洛谷 P7414

题意

有一个长度为 \(n\) 的序列 \(a\)，你有一个序列 \(b\)，最开始序列 \(b\) 中的所有数字都是 \(0\)，你每次可以选择一段区间 \([l, r]\)，并将这段区间的所有 \(b_i \ (l \le i \le r)\) 都变成某个数字。请问将 \(b\) 变成 \(a\) 的操作次数是多少？

思路

\(dp_{i, j}\) 表示将 \(b_i \sim b_j\) 变成 \(a_i \sim a_j\) 所需要的最少操作次数。

如果 \(a_i = a_j\)，说明我们能先将 \(i, j\) 染成这种颜色，就不用在自己所在的子区间多花费一次操作了。

代码

cin >> n;
for (int i = 1; i <= n; i++) {
  cin >> a[i], dp[i][i] = 1;
  for (int j = i + 1; j <= n; j++) {
    dp[i][j] = n + 1;
  }
}
for (int len = 2; len <= n; len++) {
  for (int l = 1, r = len; r <= n; l++, r++) {
    for (int k = l; k < r; k++) {
      dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] - (a[l] == a[r]));
    }
  }
}
cout << dp[1][n];

树形 dp

我们先看一道题：

洛谷 P1122

题意

给定一颗有 \(n\) 个结点的树，求出这棵树的最大子树和。

思路

令 \(dp_i\) 表示以 \(i\) 为根的子树的最大子树和。

既然要以 \(i\) 为根，那么，最开始，\(dp_i = a_i\)。

对于 \(i\) 的每一个儿子 \(j\)，如果 \(dp_j < 0\)，我们就没必要选择 \(j\) 了。

所以有转移：

\[dp_i = a_i + \sum\limits _{(i, j) \in E} max(0, dp_j) \]

代码

void dfs(int t, int fa) {
  dp[t] = a[t];
  for (int i : g[t]) {
    if (i != fa) {
      dfs(i, t), dp[t] += max(0, dp[i]);
    }
  }
  ans = max(ans, dp[t]);
}

洛谷 P1352

题意

给定一颗有 \(n\) 个结点的树，编号为 \(i\) 的结点有一个价值 \(a_i\)，你可以选择一些结点，使得它们的价值之和最大，但是，如果你选择了 \(i\)，那么你就不能选择点 \(i\) 的所有儿子了。

思路

\(dp_{u, 0 / 1}\) 表示在 \(u\) 的子树内，不选择 / 选择 \(u\) 可以得到的最大价值之和。

那么，如果当前选择 \(u\)，它的所有儿子 \(v\) 都不能选择了，也就是说，\(dp_{u, 1} = a_u + \sum\limits_{(u, v) \in E} dp_{v, 0}\)。

否则，如果不选择 \(u\)，那么它的所有儿子 \(v\) 可选可不选，取两种情况的最优解即可，所以，\(dp_{u, 0} = \sum\limits_{(u, v) \in E} max(dp_{v, 0}, dp_{v, 1})\)。

代码

void dfs(int t, int fa) {
  dp[t][1] = a[t];
  for (int i : g[t]) {
    if (i != fa) {
      dfs(i, t);
      dp[t][1] += dp[i][0];
      dp[t][0] += max(dp[i][0], dp[i][1]);
    }
  }
}

洛谷 P2015

题意

给定一颗有 \(n\) 个结点的二叉树，编号为 \(1 \sim n\)，树根编号一定是 \(1\)。

给定需要保留的树枝数量，求出最多能留住多少苹果。

思路

我们令 \(dp_{i, j}\) 表示在 \(i\) 的子树内保留 \(j\) 根树干可以得到的最多的苹果数量。

由于这是一颗二叉树，所以我们令 \(ls(i)\) 表示 \(i\) 的左儿子的编号，\(lc(i)\) 表示 \(i\) 连向 \(ls(i)\) 的这条边上的苹果数量，\(rs(i)\) 表示 \(i\) 的右儿子的编号，\(rc(i)\) 表示 \(i\) 连向 \(rs(i)\) 的这条边上的苹果数量。

所以就有转移：

\[dp_{i, j} = \max\{dp_{ls(i), j - 1} + lc(i), dp_{rs(i), j - 1} + rc(i), dp_{ls(i), k - 1} + lc(i) + dp_{rs(i), j - k - 1} + rc(i) \ (1 \le k < j)\} \]

代码

void dfs(int x, int fa) {
  int ls = 0, rs = 0, lc = 0, rc = 0;
  for (Edge y : g[x]) {
    if (y.x != fa) {
      dfs(y.x, x);
      if (ls) rs = y.x, rc = y.c;
      else ls = y.x, lc = y.c;
    }
  }
  for (int i = 1; i <= k; i++) {
    dp[x][i] = max(dp[ls][i - 1] + lc, dp[rs][i - 1] + rc);
    for (int j = 1; j < i; j++) {
      dp[x][i] = max(dp[x][i], dp[ls][j - 1] + dp[rs][i - j - 1] + lc + rc);
    }
  }
}

状压 dp

状压 dp 就是将状态压缩成一个整数来优化转移。

先看一道题目：

CSES 1690

题意

\(m\) 条单向航线连接着 \(n\) 座城市。你想要从第一座城市出发，经过每座城市恰好一次后，抵达第 \(n\) 座城市。请问你有几种不同的可选路线？

思路

\(dp_{i, j}\) 表示当前这 \(n\) 座城市被遍历的状态为 \(i\)，最后一个到达的点为 \(j\) 时的可选路径的数量。

所以，就有转移：

dp[i | (1 << (k - 1))][k] = (dp[i | (1 << (k - 1))][k] + dp[i][j] * f[j][k] % mod) % mod;

f[j][k] 表示 \(j\) 到 \(k\) 的路径数量。

dp[1][1] = 1;
for (int i = 0; i < (1 << n) - 1; i++) {
  for (int j = 1; j <= n; j++) {
    if (dp[i][j]) {
      for (int k = 1; k <= n; k++) {
        if (f[j][k] && (i & (1 << (k - 1))) == 0) {
          dp[i | (1 << (k - 1))][k] = (dp[i | (1 << (k - 1))][k] + dp[i][j] * f[j][k] % mod) % mod;
        }
      }
    }
  }
}
cout << dp[(1 << n) - 1][n];

一些 dp 习题

CESE 1130 Tree Matching

题意

给定包含 \(n\) 个结点的树。

匹配是一个边集，并且树上的每个点在这个边集中最多连接 \( 1\) 条边。请你求出匹配中最多有多少条边。

\(1 \le n \le 2 \times 10 ^ 5\)

思路

首先，这个题目每次选取的是一条边，那么这一条边用父亲还是儿子来表示呢？

当然是用 儿子 来表示啦！因为每个结点只有一个父亲。

所以，\(dp _ {i, 0 / 1}\) 表示第 \(i\) 个结点联想父亲的那条边是否选择时，\(i\) 的子树上最多连了多少条边。

那么，我们就分两种情况来处理。

设当前搜索到的点的编号为 \(u\)，则：

\[dp _ {u, 0} = \max \{\sum _ {v \in son _ u} dp _ {v, 0}, \max _ {v \in son _ u} \{\sum _ {v' \in son _ u} dp _ {v', 0} - dp _ {v, 0} + dp _ {v, 1}\}\} \]

\[dp _ {u, 1} = \sum _ {v \in son _ u} dp _ {v, 0} \]

在选择的情况中，因为点 \(u\) 已经连出去了一条边，所以它和它的所有儿子的边都不能连。

如果不选择，那么就只能在儿子中选择一条边连，或者不连。

那么最后的答案是什么呢？

因为 \(1\) 是根节点，没有父亲，所以直接输出 \(dp _ {1, 0}\) 即可。

代码

#include <bits/stdc++.h>

using namespace std;

const int N = 2e5 + 10;

int n, dp[N][2];

vector<int> g[N];

void dfs(int t, int fa) {
  dp[t][1] = 1;
  int s = 0;
  for (int i : g[t]) {
    if (i != fa) {
      dfs(i, t);
      dp[t][1] += dp[i][0], s += dp[i][0];  // 处理选择
    }
  }
  dp[t][0] = s;
  for (int i : g[t]) {
    if (i != fa) {
      dp[t][0] = max(dp[t][0], s - dp[i][0] + dp[i][1]);  // 处理不选择
    }
  }
}

int main() {
  ios::sync_with_stdio(0);
  cin.tie(0), cout.tie(0);
  cin >> n;
  for (int i = 1; i < n; i++) {
    int a, b;
    cin >> a >> b;
    g[a].push_back(b), g[b].push_back(a);  // 建树
  }
  dfs(1, 0);
  cout << dp[1][0];  // 输出答案
  return 0;
}

abc 231 e

题意

有 \(n\) 种硬币，面值分别为 \(A_1, A_2, \dots A_N\) 元，其中 \(1 = A_1 < A_2 < A_3 \dots < A_N\)，并且对于 \(1 \le i \le N - 1\) 的所有 \(i\) 都有 \(A_{i + 1}\) 是 \(A_i\) 的倍数。

现在要用这些硬币支付 \(X\) 元，请你求出支付和找零的硬币数量的和的最小值。

  • \(1 \le N \le 60\)。

  • \(1 = A_1 < \dots < A_N \le 10 ^ {18}\)。

  • \(1 \le X \le 10 ^ {18}\)。

思路

首先，这个题目有一个很明显会超时还有可能会爆空间的做法，完全背包。

\(dp_i\) 表示凑出 \(i\) 元的最少硬币数量。

转移为：

\[dp_i = \min _ {j = 1} ^ n \{dp_{i - a_j} + 1\} \]

因为支付的钱数最多为 \(2 \times X\) 元（如果支付 \(2 \times X\) 元，就需要找零 \(X\) 元，也是凑出 \(X\) 元，还需要额外加上凑出 \(2 \times X\) 元的硬币数量，很明显会比直接凑出 \(X\) 元更差），所以空间复杂度为 \(O(2 \times X)\)。

但是 \(X\) 有 \(10 ^ {18}\) 那么大，根本不能用数组存下来，所以我们可以用 map 来实现。

但是，就算空间的问题解决了，时间也救不回来。

dp 的时间复杂度为 \(O(2 \times X)\)，也就是 \(O(X)\)。

计算答案的时间复杂度为 \(O(X)\)。

总时间复杂度为 \(O(X)\)，完全无法接受。

所以，我们要考虑其他方法。

其实可以发现，题目中几乎所有条件我们都用上了，但还有一句话：对于 \(1 \le i \le N - 1\) 的所有 \(i\) 都有 \(A_{i + 1}\) 是 \(A_i\) 的倍数。 这句话我们一直都没有用上，那么，这又代表了什么呢？

题目里还有一个条件： \(1 = A_1 < A_2 < A_3 \dots < A_N\)
。

这代表着任何一个数都可以被表示出来，而又有 \(A_{i + 1}\) 是 \(A_i\) 的倍数这个条件，所以可以发现，我们可以将 \(X\) 变成一个不知道是什么进制的数，而它对应的硬币数量就是他各位数字之和。

所以我们可以列这样一个表格：

令 \(B_i = A_{i + 1} \div A_i (1 \le i \le N - 1)\)

位号 N \(\dots\) 2 1 0
位权 \(A_N\) \(\dots\) \(A_3\) \(A_2\) \(A_1\)
数值 \(C_N = x \div B_1 \dots \div B_N\) \(\dots\) \(C_3 = x \div B_1 \div B_2 \mod B_3\) \(C_2 = X \div B_1 \mod B_2\) \(C_1 = X \mod B_1\)

所以，对于第 \(i\) 位来说，这意味可以选择用 \(C_i\) 个 \(A_i\)，也可以用 \(1\) 个 \(A_{i + 1}\) 和 \(B_i - C_i\) 个 \(A_i\)。

\(dp_{i, 0 / 1}\) 表示用前 \(i\) 种硬币凑出（不出）前 \(i\) 位所用的硬币的最小数量（描述的很奇怪）

所以有转移：

\[dp_{i, 0} = \min \{dp_{i - 1, 0}, dp_{i - 1, 1}\} + C_i \]

来解释一下吧，就是如果第 \(i\) 位要用 \(C_i\) 个 \(A_i\) 来凑的话，那么就直接取上一位的最小硬币数量，再加上 \(C_i\) 即可。

那么，这里就有一个问题了，如果第 \(i - 1\) 位是用 \(1\) 个 \(A_i\) 和 \(B_{i - 1} - C_{i - 1}\) 个 \(A_{i - 1}\) 凑出来的话，\(dp_{i - 1, 1}\) 不应该在加 \(1\) 吗？

这么想也没问题，主要是写法的不同，我是把这个 \(1\) 放在 \(dp_{i - 1, 1}\) 中加的。

\[dp_{i, 1} = \min \{dp_{i - 1, 0} + 1, dp_{i - 1, 1} - 1\} + B_i - C_i \]

我们先看 \(dp_{i - 1, 0} + 1\)，这里的 \(dp_{i - 1, 0}\) 就是第 \(i - 1\) 位不借位的最少硬币数量，再 \(+ 1\) 则是因为当前这一位要再借一位。

再看 \(dp_{i - 1, 1} - 1\)，这个就有一点点不好懂了。

我们先将这个转移换一种方式写出来：

\[dp_{i, 1} = \min \{dp_{i - 1, 0} + 1 + B_i - C_i, dp_{i - 1, 1} - 1 + B_i - C_i\} \]

其实这个式子应该是 \(dp_{i - 1, 1} - 1 + 1 + (B_i - C_i - 1)\)，第一个 \(- 1\) 是因为在前 \(i - 1\) 位已经借过一次了，而这里又要借，所以要把之前借的那一位先去掉，\(+ 1\) 是因为又要再借一位，\(B_i - C_i - 1\) 是第 \(i\) 种硬币需要找零的数量，因为第 \(i - 1\) 位借了一个，所以第 \(i\) 位所需要的硬币数量就变成 \(C_i + 1\) 了，所以就是 \(B_i - (C_i + 1)\)，也就是 \(B_i - C_i - 1\)。

所以总时间复杂度为 \(O(n)\)，空间复杂度为 \(O(n)\)。

abc 237 f

题意

请你求出满足以下要求的序列数量，答案对 \(998244353\) 取模：

  • 序列长度为 \(N\)。

  • 序列中的每个整数都是 \([1, M]\) 内的一个数。

  • 序列的最长上升子序列的长度恰好为 \(3\)。

\(1 \le N \le 1000\)

\(3 \le M \le 10\)

思路

首先，我们考虑暴力：搜出所有有可能的序列，判断最长上升子序列的长度是否为 \(3\)，总时间复杂度为 \(O(N ^ {M + 2})\)，很显然，是会超时的。

所以，应该怎么优化呢？

其实可以发现，在这道题目中，组成这个长度为 \(3\) 的最长上升子序列的那 \(3\) 个数是很重要的。

所以，我们可以考虑从这三个数入手。

\(dp_{i, a, b, c}\) 表示前 \(i\) 个数中的最长上升子序列的 \(3\) 个数分别为 \(a, b, c\) 的方案数。

那么就有转移（扩散型）：

\[ dp_{i, a, b, c} \rightarrow \left \{ \begin{aligned} dp_{i + 1, x, b, c} (x \le a) \\ dp_{i + 1, a, x, c} (a < x \le b) \\ dp_{i + 1, a, b, x} (b < x \le c) \end{aligned} \right. \]

CF1077F1

题意

给定一个长度为 \(n\) 的序列 \(a\)，你需要选择 \(x\) 个元素，使得连续 \(k\) 个元素都至少有一个被选中。

你需要最大化选出来的数之和，并输出。

\(1 \le k, x \le n \le 200\)

\(1 \le a_i \le 10 ^ 9\)

思路

很明显，这题是 dp。

\(dp_{i, j}\) 表示前 \(i\) 个数中，选择 \(j\) 个的最大和。

所以就有转移：

\[dp_{i, j} = \max \limits _ {\max(0, i - k) \le l < i} \{dp_{l, j - 1} + a_i\} \]

时间复杂度为 \(O(n ^ 3)\)。

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 210, MAXX = 210;
const long long INF = -1e18;

int n, k, x, a[N];
long long dp[N][MAXX], ans;

int main() {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> k >> x;
  for (int i = 1; i <= n; i++) {
    cin >> a[i];
  }
  if (n / k > x) {  // 判断非法情况
    cout << -1;
    return 0;
  }
  for (int i = 0; i <= n; i++) { 
    for (int j = 0; j <= x; j++) {
      dp[i][j] = INF; // 初始化
    }
  }
  dp[0][0] = 0;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= x; j++) {
      for (int l = max(0, i - k); l < i; l++) {
        dp[i][j] = max(dp[i][j], dp[l][j - 1] + a[i]);  // 转移
      }
    }
  }
  for (int i = n - k + 1; i <= n; i++) {  // 统计答案
    ans = max(ans, dp[i][x]);
  }
  cout << ans;
  return 0;
}

abc 248 F

AT 链接

洛谷链接

题意

给定一个大于等于 \(2\) 的整数 \(N\) 和一个质数 \(P\)， 现在有一个有 \(2N\) 个点，\(3N - 2\) 条边的图 \(G\)。

令点的编号分别为 \(1, 2, \dots, 2N\)，令边的编号为 \(1, 2, \dots, 3N - 2\)，则按照以下方式建边得到图 \(G\)：

  • 对于 \(1 \le i \le N - 1\)，边 \(i\) 连接点 \(i\) 和 \(i + 1\)。

  • 对于 \(1 \le i \le N - 1\)，边 \(N + i - 1\) 连接点 \(N + i\) 和 \(N + i + 1\)。

  • 对于 \(1 \le i \le N\)，边 \(2N + i - 2\) 连接点 \(i\) 和 \(N + i\)。

对于 \(i = 1, 2, \dots, N - 1\)，请你求出有多少种删 \(i\) 条边的方案，使得图 \(G\) 仍然是联通的，方案数对 \(P\) 取模。

\(2 \le N \le 3000\)

\(9 \times 10 ^ 8 \le P \le 10 ^ 9\)

Sample 1

Input
3 998244353
Output
7 15

Sample 2

Input
16 999999937
Output
46 1016 14288 143044 1079816 6349672 29622112 110569766 330377828 784245480 453609503 38603306 44981526 314279703 408855776

思路

首先，我们先将 Sample 1 的图 \(G\) 建立出来。

也就是长这样的：

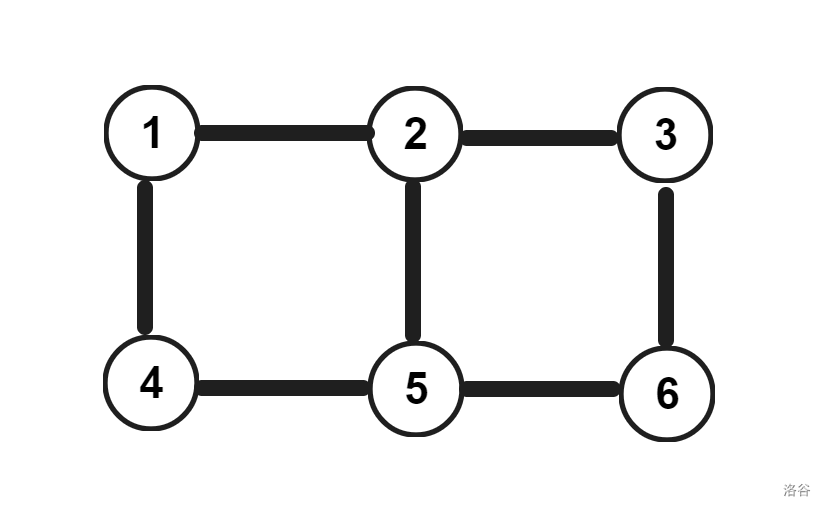
我们可以发现，这就是由很多个正方形拼成的图，每一列的两个点就是 \(i\) 和 \(i + N\)。

那么，我们先考虑一个问题，如果我们不要求删去 \(i\) 条边，而是只要满足删边使得图连通，应该怎么做呢？

我们将每一列看作成一个整体，所以对于前 \(i\) 列来说，没有连通的肯定是它的一段后缀，因为只有一段后缀是有可能通过后来加边而连通的。

所以，\(dp_{i, 0 / 1}\) 表示前 \(i\) 列是否连通的删边方案数。

那么，我们考虑转移：

如果前 \(i\) 列连通，那么：

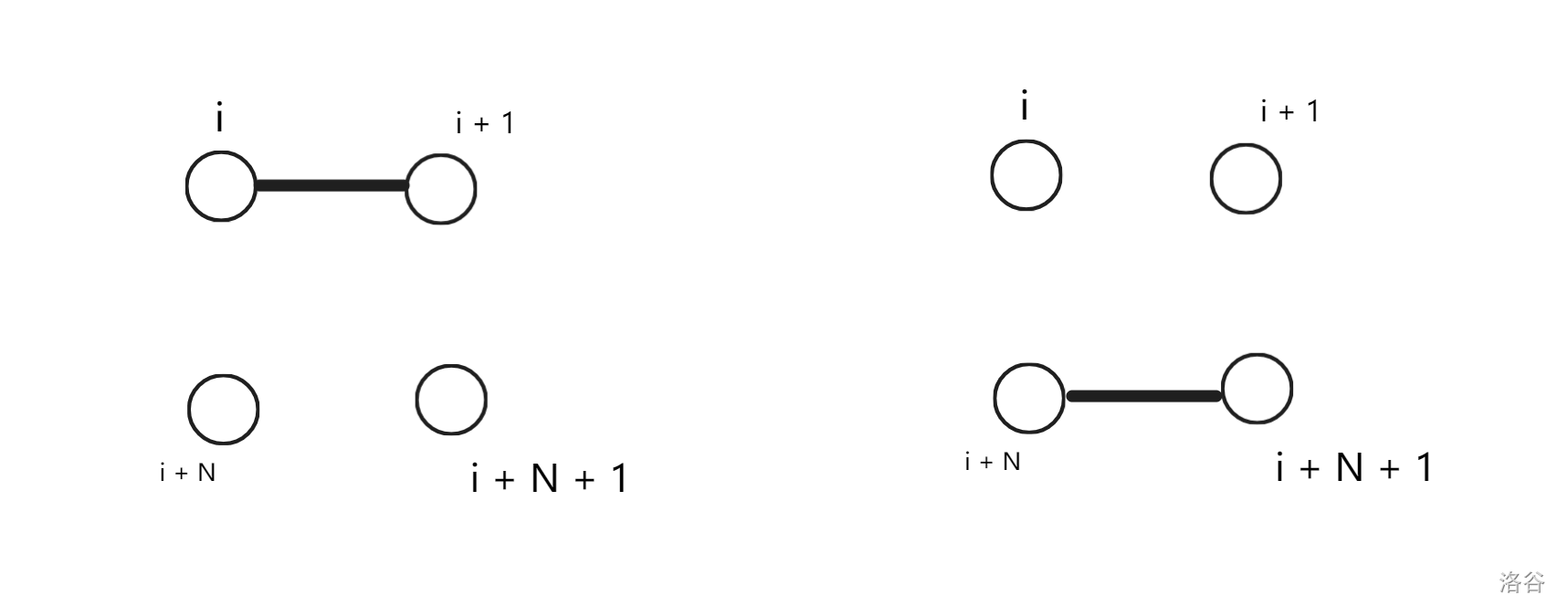
可以看出，这两种转移会使得第 \(i + 1\) 列不连通，也就是从 \(dp_{i, 1}\) 转移到 \(dp_{i + 1, 0}\)。

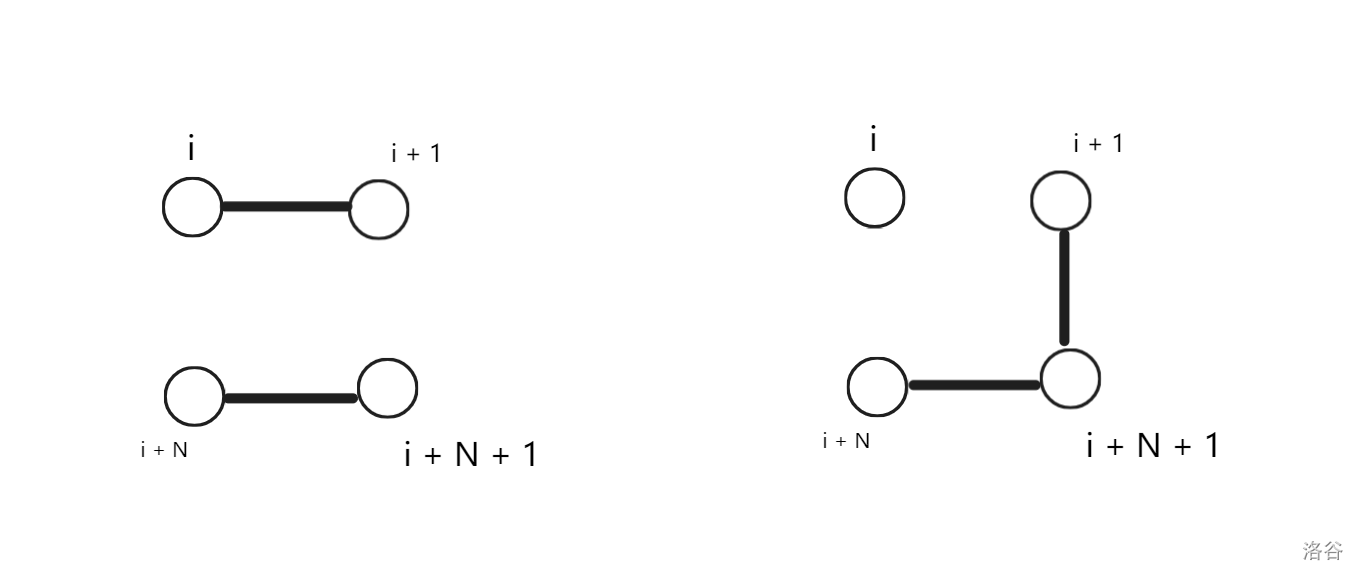
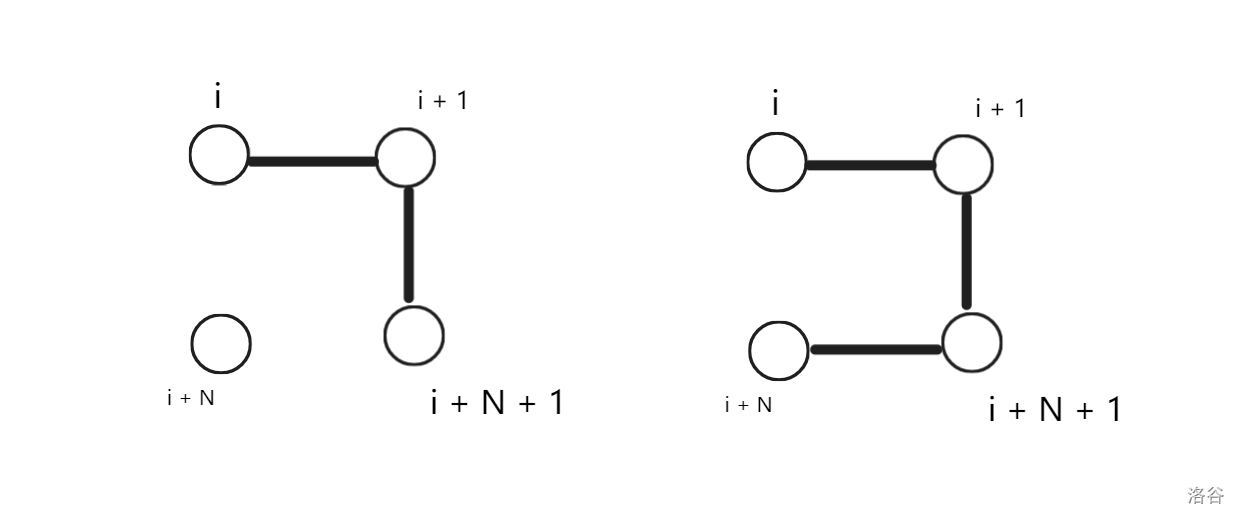
而这四种转移会使得第 \(i + 1\) 列连通，也就是从 \(dp_{i, 1}\) 转移到 \(dp_{i + 1, 1}\)。

我们再考虑第 \(i\) 列不连通：

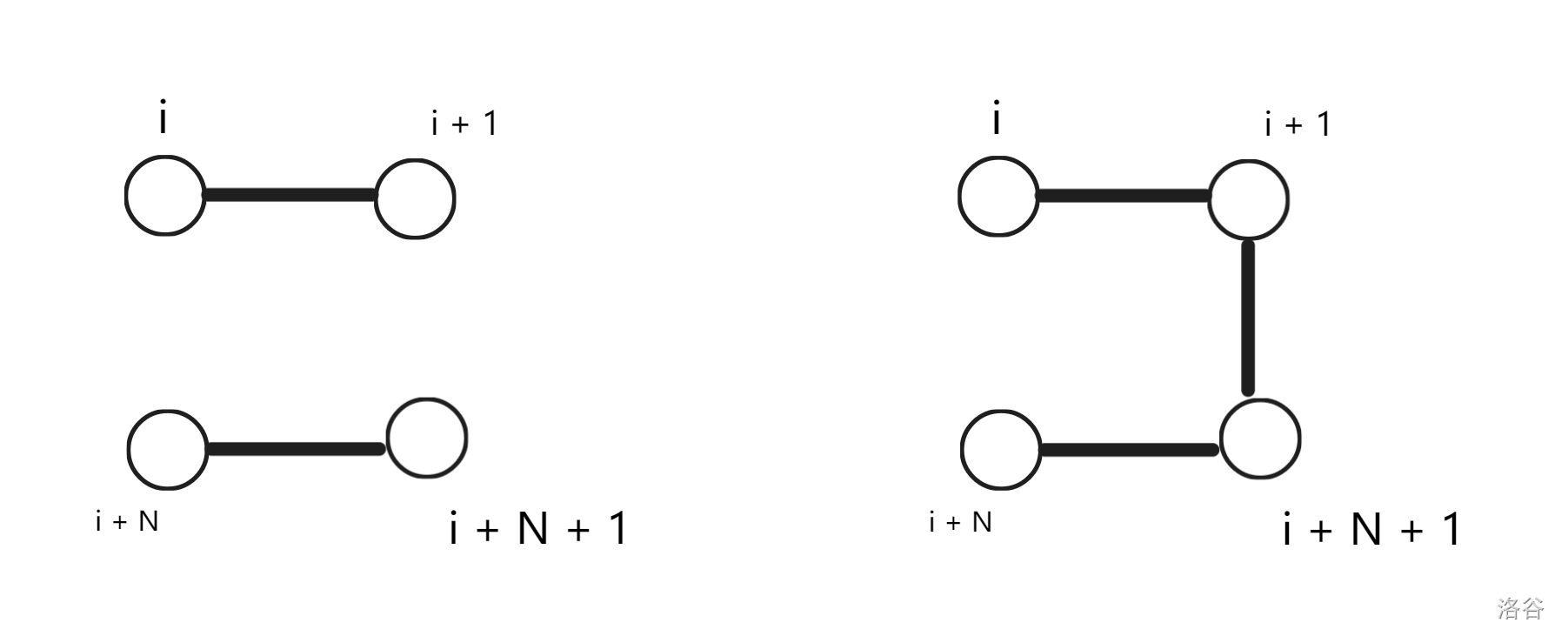
这两种转移分别会使得第 \(i + 1\) 列不连通和联通，也就是从 \(dp_{i, 0}\) 分别转移到 \(dp_{i + 1, 0}\) 和 \(dp_{i + 1, 1}\)。

那么，要求了删去的边的数量也是一样的。

\(dp_{i, j, 0 / 1}\) 表示前 \(i\) 列删去 \(j\) 条边是否连通的方案数。

那么转移就是：

\[2 \times dp_{i, j, 1} \rightarrow dp_{i + 1, j + 2, 0} \]

\[3 \times dp_{i, j, 1} \rightarrow dp_{i + 1, j + 1, 1} \]

\[dp_{i, j, 1} \rightarrow dp_{i + 1, j, 1} \]

\[dp_{i, j, 0} \rightarrow dp_{i + 1, j + 1, 0} \]

\[dp_{i, j, 0} \rightarrow dp_{i + 1, j, 1} \]

代码

#include <bits/stdc++.h>

using namespace std;

const int N = 3010;

int n, p;
long long dp[N][N][2];

int main() {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> p;
  dp[1][0][1] = dp[1][1][0] = 1;  // 初始状态
  for (int i = 1; i <= n; i++) {
    for (int j = 0; j < n; j++) {
      dp[i + 1][j + 2][0] = (dp[i + 1][j + 2][0] + 2 * dp[i][j][1]) % p;
      dp[i + 1][j + 1][1] = (dp[i + 1][j + 1][1] + 3 * dp[i][j][1]) % p;
      dp[i + 1][j][1] = (dp[i + 1][j][1] + dp[i][j][1]) % p;
      dp[i + 1][j + 1][0] = (dp[i + 1][j + 1][0] + dp[i][j][0]) % p;
      dp[i + 1][j][1] = (dp[i + 1][j][1] + dp[i][j][0]) % p;
    }
  }
  for (int i = 1; i < n; i++) {
    cout << dp[n][i][1] << ' ';
  }
  return 0;
}

abc 232 e

题意

有一个 \(n \times m\) 的矩阵，一开始有个物品放在 \((x_1, y_1)\) 上。

有 \(k\) 次操作，每次操作可以将这个物品移动到同一行或者同一列的另一个格子上。

请你求出在 \(k\) 次操作后，使得这个物品到达 \((x_2, y_2)\) 的方法有多少种，对 998244353 取模。

思路

首先，这道题我们先考虑暴力。

\(dp_{x, y, k}\) 表示走 \(k\) 步到格子 \((x, y)\) 的方案数。

那么就有转移：

\[dp_{x, y, k} = \sum _ {x' = x, y' \ne y} dp_{x', y', k - 1} + \sum _ {x' \ne x, y' = y} dp_{x', y', k - 1} \]

所以，状态总数为 \(n \times m \times k\)，每次有 \(n + m\) 种转移，总时间复杂度为 \(O(n \times m \times k \times (n + m))\)，也就是 \(10 ^ {33}\)，很明显会超时。

通过打表输出 dp 数组，我们可以发现，整个矩阵最后的结果一共可以分为四种：

  1. 起点

  2. 和起点同行的点

  3. 和起点同列的点

  4. 和起点不同行也不同列的点

所以，\(dp_{k, 0}\) 表示用 \(k\) 步走到起点的方案数，\(dp_{k, 1}\) 表示用 \(k\) 步走到与起点同行的其他的点的方案数，\(dp_{k, 2}\) 表示用 \(k\) 步走到与起点同列的其他的点的方案数，\(dp_{k, 3}\) 表述用 \(k\) 步走到和起点不同行也不同列的点的方案数。

那么，转移是什么呢？

我们可以画一个图来看一看。

\[dp_{k, 0} = dp_{k - 1, 1} \times (m - 1) + dp_{k - 1, 2} \times (n - 1) \]

\[dp_{k, 1} = dp_{k - 1, 0} + dp_{k - 1, 1} \times (m - 2) + dp_{k - 1, 3} \times (n - 1) \]

\[dp_{k, 2} = dp_{k - 1, 0} + dp_{k - 1, 2} \times (n - 2) + dp_{k - 1, 3} \times (m - 1) \]

\[dp_{k, 3} = dp_{k - 1, 1} + dp_{k - 1, 2} + dp_{k - 1, 3} \times (n + m - 4) \]

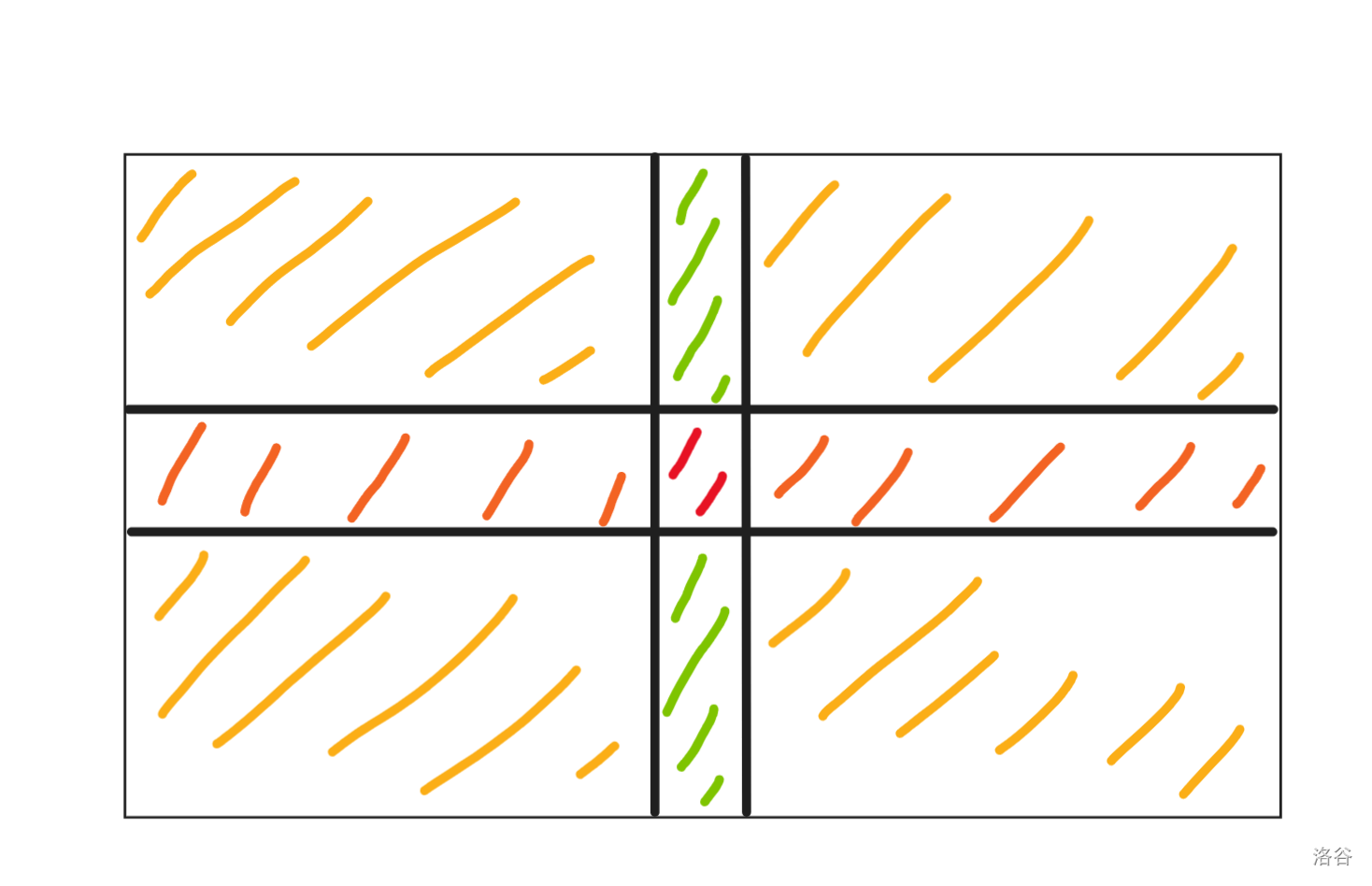
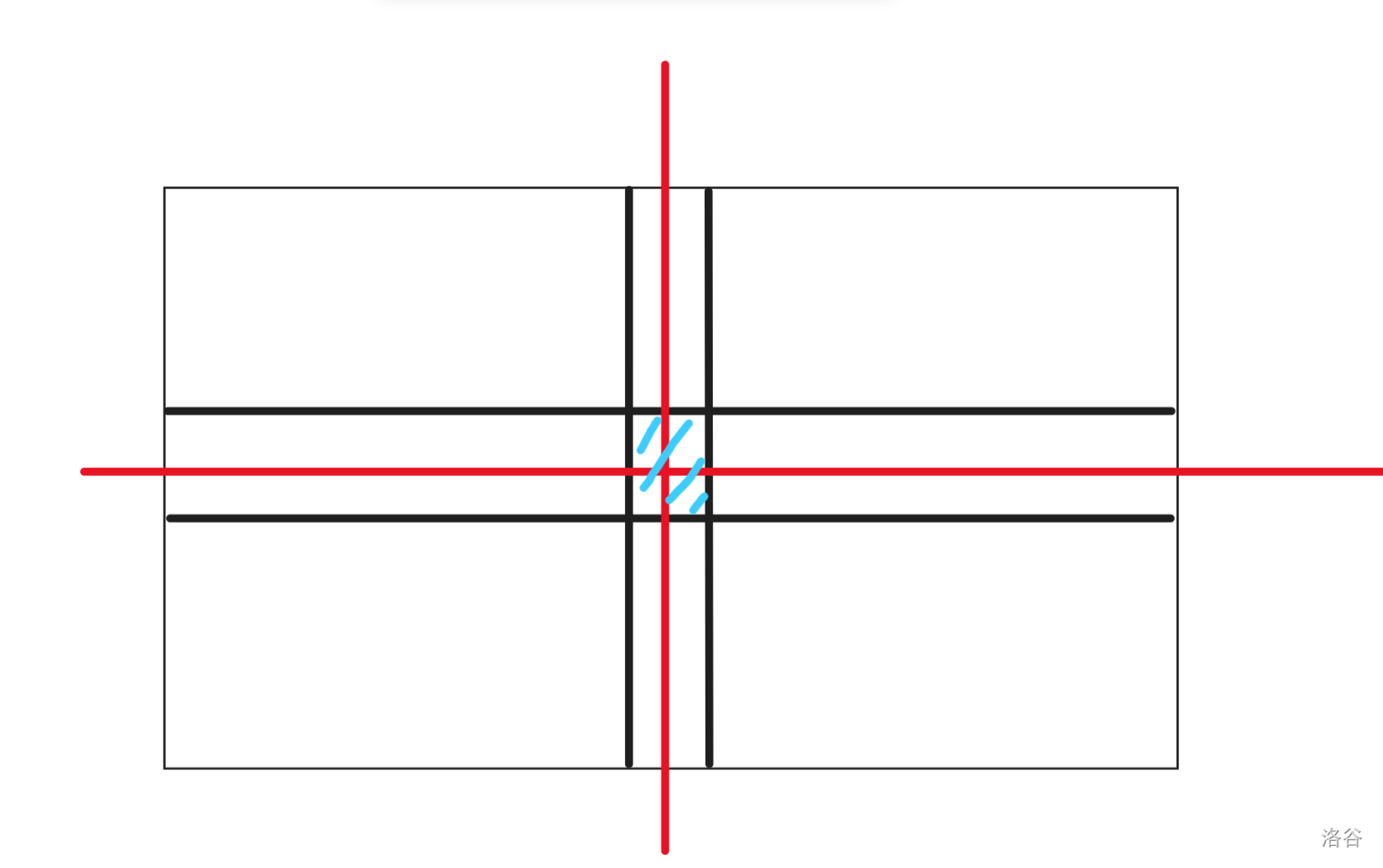
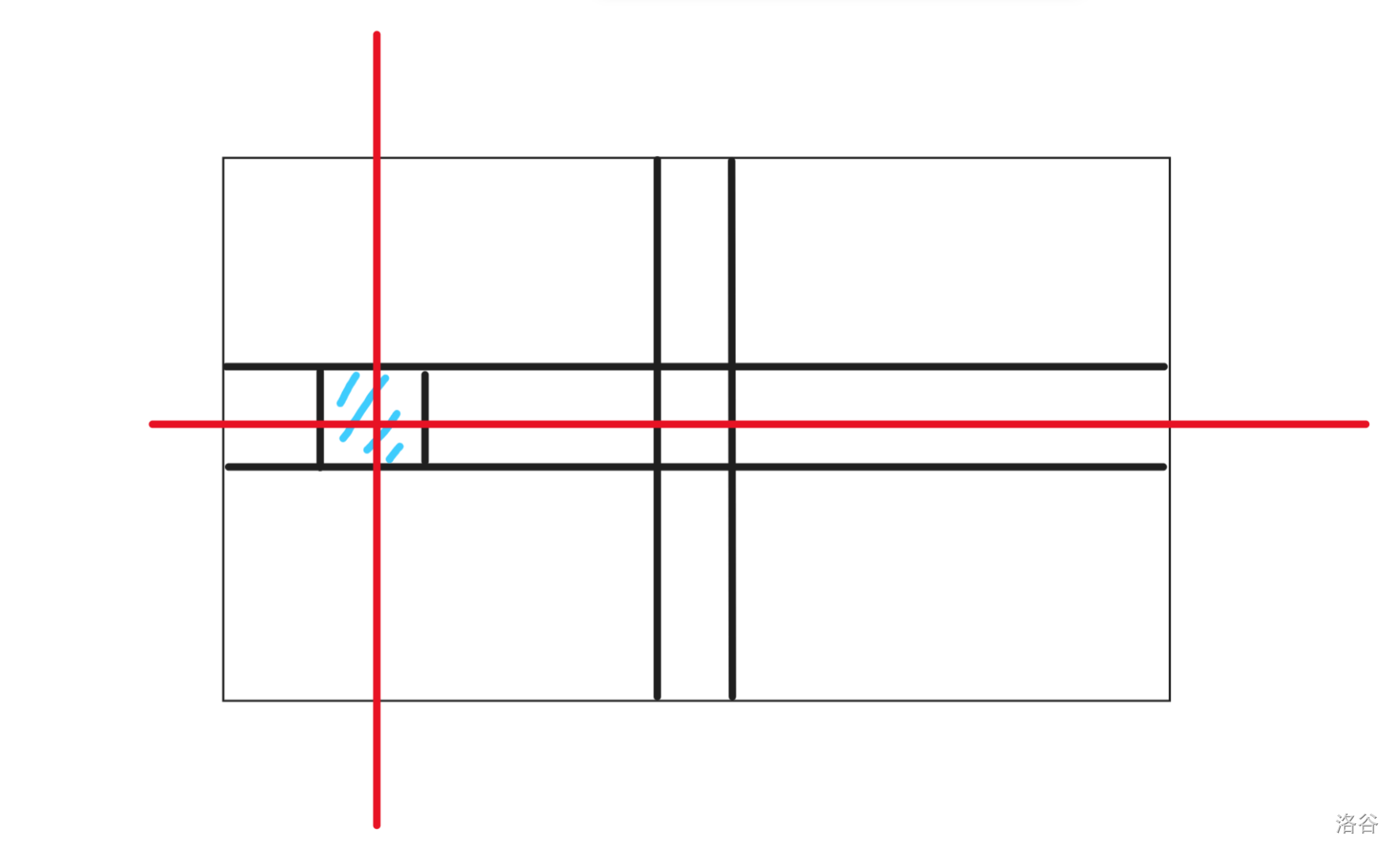
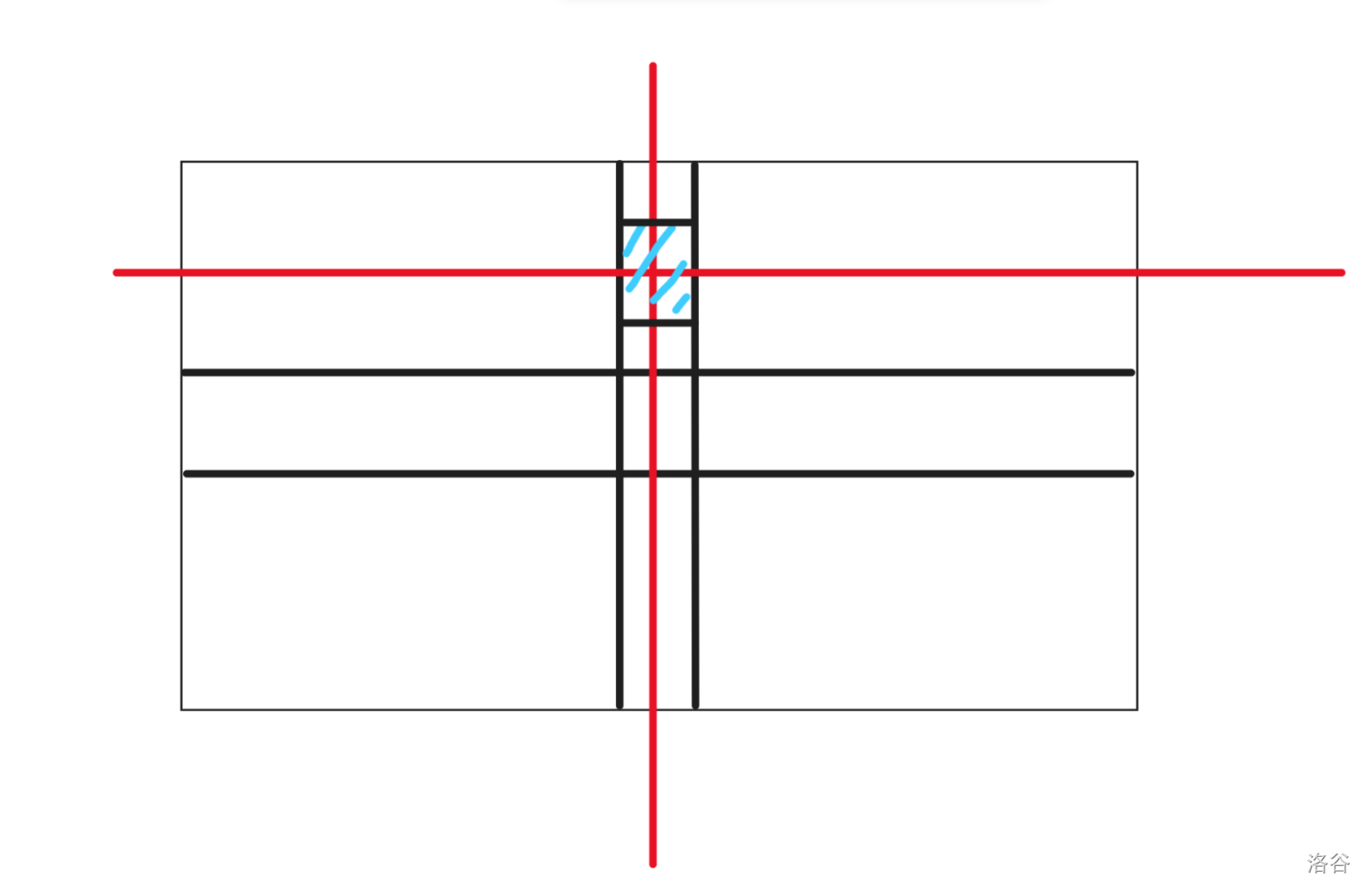
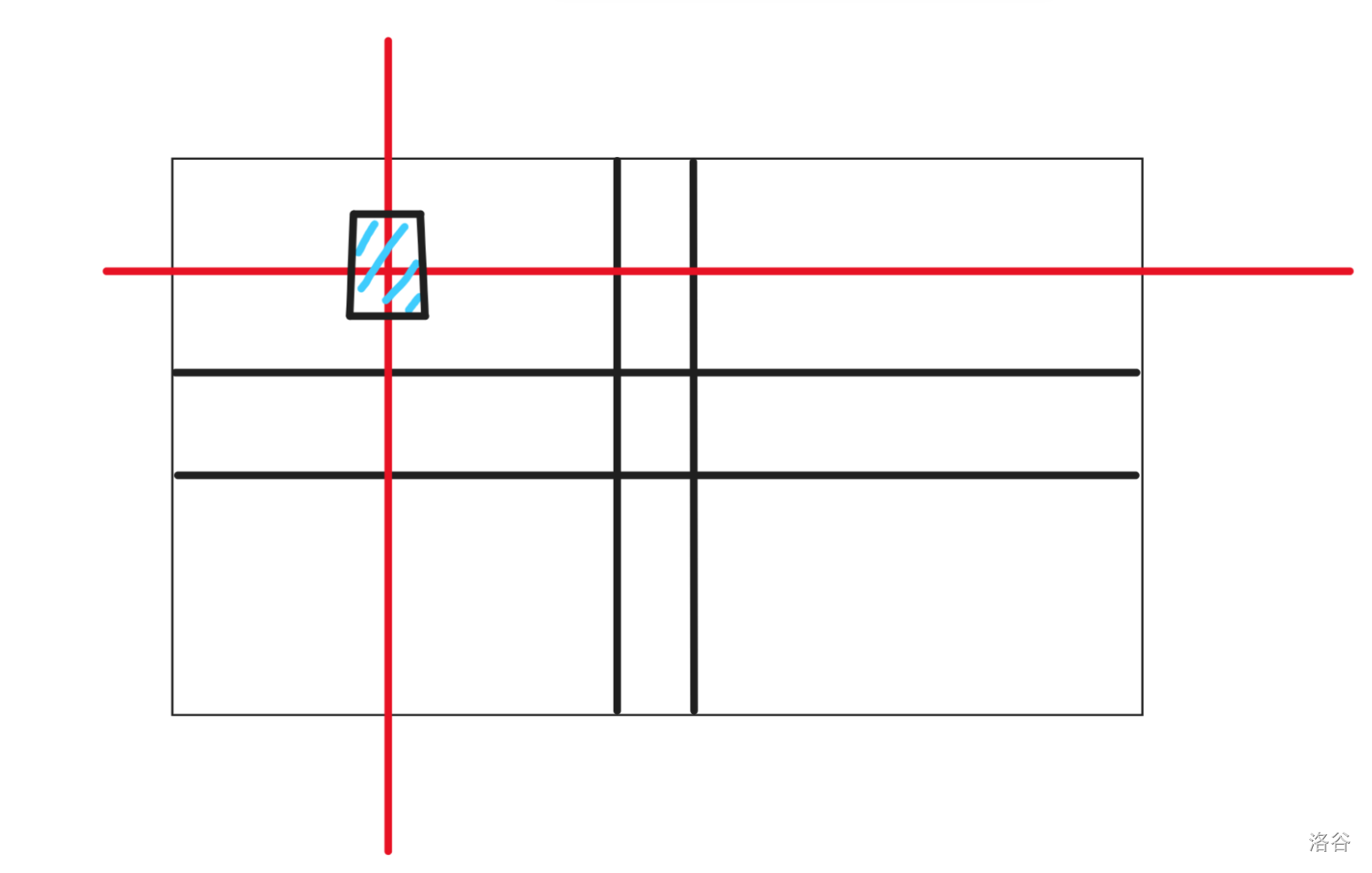
所以，时间复杂度为 \(O(k)\)。

abc 283 e

abc 283 e

题意

给定一个 \(h \times w\) 的矩阵 A，每个元素要么是 0，要么是 1。\(a_{i, j}\) 表示第 \(i\) 行第 \(j\) 列的数。

你可以做很多次操作：选择一个 \(i\) \((1 \le i \le h)\)，将第 \(i\) 行的所有 \(a_{i, j}\) \((1 \le j \le w)\) 都翻转（0 变为 1，1 变为 0）。

当 \(a_{i, j}\) 的所有相邻格子都和它不同时，称 \(a_{i, j}\) 为孤立的。

请你求出最少需要多少次操作能使得 A 中没有孤立的点，如果不能，输出 -1。

思路

首先，有一个很简单的做法，就是枚举每一行是翻还是不翻，总时间复杂度为 \({2 ^ h} \times w\)，当然，这样时间复杂度过大，所以不考虑搜索。

那既然想到搜索，就不难看出，这是个子集搜索。

既然是子集搜索，那是不是可以考虑用 dp 来实现呢？（01 背包）

dp[i][0/1][0/1] 表示第 \(i\) 行翻还是不翻，第 \(i - 1\) 行翻还是不翻，并且前 \(i - 1\) 行没有孤立点的最小翻转次数。

所以就可以得到转移方程为 dp[i][j][k] = min(dp[i - 1][k][0], dp[i - 1][k][1]) + j。

当然，在每次取最小值的时候，需要判断是否满足没有孤立点这个条件。

时间复杂度

枚举每一行，\(O(h)\)。

检查是否存在孤立点，\(O(w)\)。

总时间复杂度为 \(O(h \times w)\)。

代码

#include <bits/stdc++.h>

using namespace std;

const int H = 1010, W = 1010;

const int dx[] = {0, 1, 0, -1};
const int dy[] = {1, 0, -1, 0};

int h, w, dp[H][2][2];
bool a[H][W];

bool P(int i, int j) {  // 检查是否为孤立点
  bool flag = 0;
  for (int f = 0; f < 4; f++) {
    int nx = i + dx[f], ny = j + dy[f];
    if (1 <= nx && nx <= h && 1 <= ny && ny <= w && a[i][j] == a[nx][ny]) {
      flag = 1;
      break;
    }
  }
  return flag;
}

bool F(int i, int j, int k, int l) {  // 检查是否不存在孤立点
  for (int f = 1; f <= w; f++) {
    a[i][f] ^= j, a[i - 1][f] ^= k, a[i - 2][f] ^= l;
  }
  bool flag = 1;
  for (int f = 1; f <= w; f++) {
    flag &= P(i - 1, f);
  }
  for (int f = 1; f <= w; f++) {
    a[i][f] ^= j, a[i - 1][f] ^= k, a[i - 2][f] ^= l;
  }
  return flag;
}

int main() {
  cin >> h >> w;
  for (int i = 1; i <= h; i++) {
    for (int j = 1; j <= w; j++) {
      cin >> a[i][j];
    }
  }
  // 初始化
  for (int i = 1; i <= h; i++) {
    for (int j = 0; j < 2; j++) {
      for (int k = 0; k < 2; k++) {
        dp[i][j][k] = h + 1;
      }
    }
  }
  dp[1][0][0] = 0, dp[1][1][0] = 1;
  for (int i = 2; i <= h; i++) {
    for (int j = 0; j < 2; j++) {
      for (int k = 0; k < 2; k++) {
        for (int l = 0; l < 2; l++) {
          if (dp[i - 1][k][l] != h + 1 && F(i, j, k, l)) {
            dp[i][j][k] = min(dp[i][j][k], dp[i - 1][k][l] + j);
          }
        }
      }
    }
  }
  // 求答案
  int ans = h + 1;
  for (int i = 0; i < 2; i++) {
    for (int j = 0; j < 2; j++) {
      if (dp[h][i][j] != h + 1 && F(h + 1, 0, i, j)) {
        ans = min(ans, dp[h][i][j]);
      }
    }
  }
  cout << (ans == h + 1 ? -1 : ans);
  return 0;
}

abs 265 e

题意

Takahashi 在二维平面的原点处。有 \(N\) 次传送，每次可以选择下面三种中的一种：

  1. 从 \((x, y)\) 传送到 \((x + a, y + b)\)。

  2. 从 \((x, y)\) 传送到 \((x + c, y + d)\)。

  3. 从 \((x, y)\) 传送到 \((x + e, y + f)\)。

平面上有 \(M\) 个障碍点，不能传送到障碍点上。

请问有多少种可能的传送路径，答案对 \(998244353\) 取模。

思路

首先，我们可以想到这样一个状态，\(dp_{i, x, y}\) 表示在第 \(i\) 次操作后走到 \((x, y)\) 的方案数，再在转移的时候判断是否为障碍点。

但是，很明显，这个是不行的，因为 \((x, y)\) 太大了，存不下来。

那么，我们可以考虑另外一种角度。假设当前做了 \(i\) 次操作 \(1\)，\(j\) 次操作 \(2\)，\(k\) 次操作 \(3\)。

那么，当前所处的坐标就是 \((i \times a + j \times c + k \times e, i \times b + j \times d + k \times f)\)。

所以，我们可以枚举 \(i, j, k\)，得到当前所处的坐标，再分别进行三种转移。（也可以枚举三种操作的总次数与 \(i, j\)）

总时间复杂度为 \(O(N ^ 3)\)。

代码

#include <bits/stdc++.h>

using namespace std;

const int N = 310, mod = 998244353;

int n, m, a, b, c, d, e, f, cnt;
long long ans, dp[N][N][N];
map<pair<long long, long long>, bool> mp;

int main() {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m >> a >> b >> c >> d >> e >> f;
  while (m--) {
    int x, y;
    cin >> x >> y, mp[{x, y}] = 1;
  }
  dp[0][0][0] = 1;
  for (int i = 1; i <= n; i++) {
    for (int u = 0; u <= i; u++) {
      for (int v = 0; u + v <= i; v++) {
        int w = i - u - v;
        long long x = 1ll * u * a + 1ll * v * c + 1ll * w * e;
        long long y = 1ll * u * b + 1ll * v * d + 1ll * w * f;
        if (mp.find({x, y}) == mp.end()) {
          dp[i][u][v] = dp[i - 1][u][v];
          if (u) {
            dp[i][u][v] = (dp[i][u][v] + dp[i - 1][u - 1][v]) % mod;
          }
          if (v) {
            dp[i][u][v] = (dp[i][u][v] + dp[i - 1][u][v - 1]) % mod;
          }
          if (i == n) {
            ans = (ans + dp[i][u][v]) % mod;
          }
        }
      }
    }
  }
  cout << ans;
  return 0;
}

abc 261 e

题意

给定变量 \(X\)，有 \(N\) 种操作，第 \(i\) 次操作用一个数对 \((T_i, A_i)\) 描述：

  • \(T_i = 1, 2, 3\) 分别表示将 \(X\) 替换为 \(X \ and \ A_i, X \ or \ A_i\) 和 \(X \ xor \ A_i\)。

将 \(X\) 初始化为 \(C\)，并做以下事情：

  • 对 \(X\) 做操作 \(1\)，并输出。

  • 对 \(X\) 做操作 \(1, 2\)，并输出。

  • \(\dots\)

  • 对 \(X\) 做操作 \(1, 2, \dots, N\)，并输出。

思路

如果我们每次都从头开始做，时间复杂度会达到 \(O(N ^ 2)\)，会超时，那么我们应该怎么优化呢？

因为这里是位运算，所以我们可以考虑从每一位入手。

令 \(f_{0 / 1, i, j}\) 表示 \(X\) 的第 \(i\) 位为 \(0 / 1\)，做到第 \(j\) 次操作时的答案。

那么，每次询问只要枚举当前的 \(X\) 的每一位，将答案合并起来即可。

代码

#include <iostream>

using namespace std;

const int N = 2e5 + 10;

int n, c, t[N], a[N], f[2][35][N], l;

int main() {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> c;
  for (int i = 1; i <= n; i++) {
    cin >> t[i] >> a[i];
  }
  for (int i = 0; i < 2; i++) {
    for (int j = 0; j < 30; j++) {
      f[i][j][0] = i;
      for (int k = 1; k <= n; k++) {
        int v = (a[k] >> j) & 1;
        if (t[k] == 1) {
          f[i][j][k] = f[i][j][k - 1] & v;
        } else if (t[k] == 2) {
          f[i][j][k] = f[i][j][k - 1] | v;
        } else {
          f[i][j][k] = f[i][j][k - 1] ^ v;
        }
      }
    }
  }
  for (int i = 1; i <= n; i++) {
    int ans = 0;
    for (int j = 0, k = c; j < 30; j++, k >>= 1) {
      ans += f[k & 1][j][i] * (1 << j);
    }
    cout << ans << '\n';
    c = ans;
  }
  return 0;
}

洛谷 P5017

题意

有一辆摆渡车，它从 \(A\) 点出发，前往 \(B\) 点，每走一个来回需要 \(m\) 分钟。

有 \(n\) 个人， 第 \(i\) 个人会在时刻 \(t_i\) 到达 \(A\) 点，摆渡车需要将他们全部送到 \(B\) 点。

现在可以任意安排摆渡车的出发时间，请问这些人的等车时间的和最小是多少。

思路

30 分

枚举发车时间，记录等待时间最小值。

时间复杂度

枚举时间，\(O(\max \{ t_i\} + m)\)。

记录最小值，\(O(n ^ 2)\)。

总时间复杂度为 \(O(T \times n ^ 2)\)。

空间复杂度

一维 \(dp\) 数组记录最小值，\(O(T)\)。

代码
#include <bits/stdc++.h>

using namespace std;

const int N = 510, T = 4e6 + 10;

int n, m, t[N];
long long dp[T], sum = LLONG_MAX;

long long C(int x, int y){  // 枚举区间内的时间
  long long ans = 0;
  for (int i = 1; i <= n; i++) {
    if (x <= t[i] && t[i] <= y) {
      ans += y - t[i];
    }
  }
  return ans;
}

int main(){
  cin >> n >> m;
  for (int i = 1; i <= n; i++) {
    cin >> t[i];
  }
  sort(t + 1, t + n + 1);  // 按时间先后排序
  for (int i = 0; i < t[n] + m; i++) {
    dp[i] = C(0, i);
    if (i >= m) {
      for (int j = 0; j <= i - m; j++) {
        dp[i] = min(dp[i], dp[j] + C(j + 1, i));  // 取最小值
      }
    }
    if (i >= t[n]) {
      sum = min(sum, dp[i]);
    }
  }
  cout << sum;
  return 0;
}

50 分

和 30 分想法一样，但是 \(C\) 函数时间复杂度过大，可以考虑用前缀和进行优化。

\(C(x, y) = \sum \limits _ {x \le a_i \le y} ^ {n} {(y - a_i)} = \sum \limits _ {x \le a_i \le y} ^ {n} {y} - \sum \limits _ {x \le a_i \le y} ^ {n} {a_i}\)

所以我们需要两个数组，分别记录在时刻 \(i\) 时来的人数和前 \(i\) 个 \(t_i\) 的和。

时间复杂度

枚举时间，\(O(\max \{ t_i\} + m)\)。

记录最小值，\(O(n)\)。

总时间复杂度为 \(O(T \times n)\)。

空间复杂度

一维 \(dp\) 数组记录最小值，\(O(T)\)。

代码
#include <bits/stdc++.h>

using namespace std;

const int N = 510, T = 4e6 + 10;

int n, m, t[N];
long long dp[T], sum = LLONG_MAX, s[T], cnt[T];

long long C(int x, int y){  // O(1) 查询
  if (!x) {
    return cnt[y] * y - s[y];
  } else {
    return (cnt[y] - cnt[x - 1]) * y - (s[y] - s[x - 1]);
  }
}

int main(){
  cin >> n >> m;
  for (int i = 1; i <= n; i++) {
    cin >> t[i];
    cnt[t[i]]++, s[t[i]] += t[i];
  }
  sort(t + 1, t + n + 1);
  for (int i = 1; i < t[n] + m; i++) {  // 记录前缀和
    cnt[i] += cnt[i - 1], s[i] += s[i - 1];
  }
  for (int i = 0; i < t[n] + m; i++) {
    dp[i] = C(0, i);
    if (i >= m) {
      for (int j = 0; j <= i - m; j++) {
        dp[i] = min(dp[i], dp[j] + C(j + 1, i));
      }
    }
    if (i >= t[n]) {
      sum = min(sum, dp[i]);
    }
  }
  cout << sum;
  return 0;
}

70 分

保留 50 分的优化，并添加一个新的优化。

如果时刻 \(i\) 发车，那么上一次发车一定是在 \([i - 2 \times m + 1, i - m]\) 之间。

如果上次发车在 \(i - 2 \times m\) 时，那么 \(i - m\) 时还可以发一次车，很明显，发车越频繁，等待时间越小，所以上次发车时间一定在 \([i - 2 \times m + 1, i - m]\) 之间。

时间复杂度

枚举时刻，\(O(T)\)。

枚举上次发车时间，\(O(m)\)。

总时间复杂度为 \(O(T \times m)\)。

空间复杂度

一维 \(dp\) 数组记录最小值，\(O(T)\)。

代码
#include <bits/stdc++.h>

using namespace std;

const int N = 510, T = 4e6 + 10;

int n, m, t[N];
long long dp[T], sum = LLONG_MAX, s[T], cnt[T];

long long C(int x, int y){
  if (!x) {
    return cnt[y] * y - s[y];
  } else {
    return (cnt[y] - cnt[x - 1]) * y - (s[y] - s[x - 1]);
  }
}

int main(){
  cin >> n >> m;
  for (int i = 1; i <= n; i++) {
    cin >> t[i];
    cnt[t[i]]++, s[t[i]] += t[i];
  }
  sort(t + 1, t + n + 1);
  for (int i = 1; i < t[n] + m; i++) {
    cnt[i] += cnt[i - 1], s[i] += s[i - 1];
  }
  for (int i = 0; i < t[n] + m; i++) {
    dp[i] = C(0, i);
    if (i >= m) {
      for (int j = max(0, i - 2 * m + 1); j <= i - m; j++) {  // 枚举上次发车时间
        dp[i] = min(dp[i], dp[j] + C(j + 1, i));
      }
    }
    if (i >= t[n]) {
      sum = min(sum, dp[i]);
    }
  }
  cout << sum;
  return 0;
}

加 \(O2\) 优化可以 AC

posted @ 2023-09-27 21:33  Yan719  阅读(127)  评论(0)    收藏  举报