数论
-
两个不全为零的整数a,b的最大公因子是a,b线性组合中最小的正整数.
-
如果整数a,b互素,那么存在整数m,n使得ma+nb=1.
- 令a, b, c是整数,那么(a+cb,b) =(a, b).
- 如果a, b是正整数,那么所有a, b线性组合与所有(a, b)倍数构成的集合相同.
- 如果a, az,.. a.是不全为零整数,那么(a, az,,.,a._n, a.) =(a,a2, "", an-2,(a._,a.)).
- (拉梅定理):用欧几里得算法计算两个正整数的最大公因子时, 所需的除法次数不会超过两个整数中较小的那个十进制数的位数的5倍.
- 求两个正整数a,b,a>b的最大公因子需要0((log za)')次的位运算。
![]()
- (算术基本定理)每个大于 1的正整数都可以被唯一地写成素数的乘积,在乘积中的素因子按照非降序排列.
![]()
![]()
- 如果a和b是正整数,则[a,b]=ab/(a,b)
![]()
整数Fn=2^2n+1被称为费马数.
- 费马数F。=2*+1的每个素因子都形如2^(n+2)*k+1.
![]()
![]()


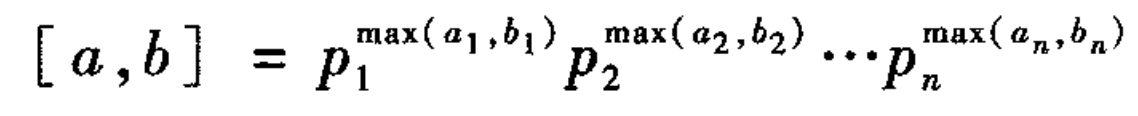




 浙公网安备 33010602011771号
浙公网安备 33010602011771号