网络流
模拟赛考了三道网络流,场上只看出来一道网络流……一点板子都不会写了,遂复习重学+补博客的坑
upd:2025.3.22 突然发现我的当前弧优化写的不对,必须写在判断条件的下面,否则有可能在回溯的时候往回跳
前置
网络流是一个有源点s和汇点t的有向图
容量限制: 对于每条边,都有一个 \(f(u,v)\) 表示它上的流,同有一个 \(c(u,v)\) 表示它的容量。\(f(u,v)\leq c(u,v)\) ,一条边的流不能超过它的容量。
斜对称性: \(w(u,v)=-w(v,u)\)
流守恒: 除非是源点或汇点,剩下所有节点流入和流出的流量相等。源点是产生流量的地方,汇点是流量流至的地方。
剩余流量: 边的剩余流量是 \(c_f(u,v)=c(u,v)-f(u,v)\) ,这定义了剩余网络,它显示可用的容量的多少。注意,即使元网络中 u->v 没有边,在剩余网络中仍可能有 u->v 的边。因为相反方向的流抵消,减少由 v->u 的流等于增加 u->v 的流。
增广路: 就是一条路径,它的起点是s,终点是t,且它经过的边的剩余流量均大于0,表示沿这条路径发送更多流是可能的。当且仅当剩余网络没有增广路时,达到最大流。
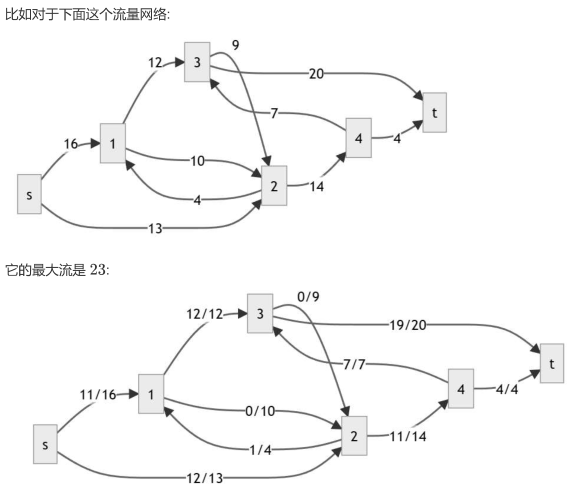
最大流
非常顾名思义,就是求s到t的最大可行流
首先,引入反向边。如果我们没有反向边,那么如果直接给流量,可能不会是整体最优决策。那么我们在给流量的时候,给当前边容量减掉流量,反向边加上流量,这样就可以在之后的操作中,通过走反向边,给程序“反悔”的机会。
dinic
dinic又称为“Dinic阻塞流算法”,该算法的关键就在于“阻塞流”
这里我们说的最短路是01最短路,即路径上的边数。我们考虑每次增广最短路上的边(这个跟时间复杂度证明有关)
这里我们引入“分层图”,大概就是对于每个点,按照s到它的最短路长度分组,最短路长度相等的为“一组”或“一层”。这个分层也可以理解为深度。
建图后我们发现,所有存在于分层图上的残余边都在一条残量网络的最短路上。因为不用担心在处理分层图时流被反向退回,我们放心地只用一遍dfs来增广就好了。(增广就是找到一条增广路,并让它流它上面能流的最大流量)
但这并不意味我们在边上处理流量的时候不用管反向边,反向边的残量变更还是要计算的。因为以后的dfs可能会把流再推回去。
我们发现,当把分层图上的最大流完全增广后,s和t在分层图上一定不连通,我们称其为阻塞增广,这样增广出来的流就是阻塞流。
dinic主要由一个bfs和一个dfs组成,其中bfs用于寻找最短路;dfs用于在可行增广路中寻找最小容量,即寻找增广路最多能流的流量。
当前弧优化
保证复杂度的一个东西
我们定义一个now数组,它最初就是h数组,即邻接表存图的头指针。我们在dfs时,从x到了第i条边,就说明前i-1条边已经被榨干了,那么不妨直接改now[x]=i,下次访问从x出发的节点时就可以直接到这里。
这个就是因为,前面所说的“阻塞流”。因为每次跑阻塞流都会把当前路径断开,即,不再能从s到达t,所以这些跑过的边是没用的。
\(O(n^2m)\) 但玄学上界,指复杂度很松,一般都能跑。。
还是贴一下时间复杂度证明吧:

void add(int u,int v,int val){
nxt[++cnt]=h[u],to[cnt]=v,h[u]=cnt,w[cnt]=val;
nxt[++cnt]=h[v],to[cnt]=u,h[v]=cnt,w[cnt]=0; //有向图!
}
int bfs(){
memset(dep,0,sizeof(dep));
queue<int>q;
q.push(s);
dep[s]=1;
now[s]=h[s];
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=h[x];i;i=nxt[i]){
int y=to[i];
if(w[i]>0&&dep[y]==0){//直接考虑能走的边
q.push(y);
now[y]=h[y];//当前弧优化
dep[y]=dep[x]+1;//分层图
if(y==t) return 1;
}
}
}
return 0;
}
int dfs(int x,int sum){//这里,sum:整条路的最大贡献流量
if(x==t) return sum;
int k,res=0;
for(int i=now[x];i&∑i=nxt[i]){
int y=to[i];
if(w[i]>0&&(dep[y]==dep[x]+1)){//保证是最短路+能走
now[x]=i;//当前弧优化,走过的
k=dfs(y,min(sum,w[i]));//k流过的流量
if(k==0) dep[y]=0;//剪枝,增广完毕
w[i]-=k,w[i^1]+=k;//正反向边
res+=k;//经过该点的流量和
sum-=k;//经过该点当前剩余流量
}
}
return res;
}
void dinic(){
while(bfs()){
ans+=dfs(s,inf);
}
}
费用流
也叫最小费用最大流。保证解是最大流的情况下,费用最大/小。
怎么说,就是把bfs动点手脚,改成spfa,支持最长路最短路就行。
对EK或dinic的最短路改成spfa都行。dinic更快一点,而且和最大流差别不大,就是bfs的按01最短路分层改成了按SPFA最短/长路分层。然后后面为了处理0费用边必须写一个vis,否则会寄。
\(O(n^2m^2)\)
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e3+5,maxm=5e4+5,inf=0x3f3f3f3f;
int n,m,h[maxn],to[maxm<<1],nxt[maxm<<1],cnt=1,w[maxm<<1],f[maxm<<1];
int dis[maxn],vis[maxn],now[maxn],mcost,mflow,s,t;
void add(int u,int v,int val,int flow){
nxt[++cnt]=h[u],to[cnt]=v,h[u]=cnt,w[cnt]=val,f[cnt]=flow;
nxt[++cnt]=h[v],to[cnt]=u,h[v]=cnt,w[cnt]=-val,f[cnt]=0;
}
bool SPFA(){
memset(dis,0x3f,sizeof(dis));
queue<int>q; q.push(s);
dis[s]=0,vis[s]=1;
while(q.size()){
int x=q.front(); q.pop();
vis[x]=0,now[x]=h[x];
for(int i=h[x];i;i=nxt[i]){
int y=to[i];
if(f[i]>0&&dis[x]+w[i]<dis[y]){
dis[y]=dis[x]+w[i];
if(!vis[y]) q.push(y),vis[y]=1;
}
}
}
return dis[t]!=inf;
}
int dfs(int x,int sum){
if(x==t) return sum;
int k,res=0; vis[x]=1;//处理0费用边,因为后面有一个dis[y]==dis[x]+w[i]否则会来回跑
for(int i=now[x];i&∑i=nxt[i]){
int y=to[i];
if(!vis[y]&&f[i]>0&&dis[y]==dis[x]+w[i]){
now[x]=i;
k=dfs(y,min(sum,f[i]));
if(!k) dis[y]=0;
mcost+=k*w[i];
f[i]-=k,f[i^1]+=k;
sum-=k,res+=k;
}
}
vis[x]=0;
return res;
}
void dinic(){
while(SPFA()){
mflow+=dfs(s,inf);
}
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1,u,v,val,flow;i<=m;i++){
scanf("%d%d%d%d",&u,&v,&flow,&val);
add(u,v,val,flow);
}
dinic();
printf("%d %d",mflow,mcost);
return 0;
}
最小割
割: 将所有节点划分成S,T两个集合,源点属于S,汇点属于T。相当于一刀切。
割的径流量: 集合S和T间连接的边中,从S到T边的容量之和。最小割为容量最小的割。
定理:最大流=最小割
感性理解就行(
闲话:
第一眼看题,不一定能看出来是网络流,甚至可能是把一个数据类的抽象到图论上。总之很巧妙,像dp。就先看限制约束条件,可以先思考连边,然后考虑是最大流、最小割还是什么总体-局部的转换,最后建图。
有一个最大权闭合子图,套路性的正边-源点,负边-汇点,答案为正边权和-最小割。
求解一条边能否在最小割和是否一定在最小割中的问题时,考虑在最终的残量网络上用 tarjan 求解。
上下界网络流(可行、最大、最小、费用流)
主要思想就是先让它直接流下界的流量,然后如果是有源汇的就连汇点t到源点s(因为流量应该相等),多余或不足的流量从新的源点汇点S、T补(这里直接理解为“令”它的出/入流量为什么),然后跑最大流,如果把新源点汇点的边跑满,则可行。
最大流就是在残量网络上s-t跑最大流+可行流。
最小流就是删去和S、T连边以及t-s后跑最大流,w(t-s)-最大流。
费用流基本是可行费用流,套板子即可。
这个算法真的,不太用动脑(?只要能用的,按题意模拟即可。(算是网络流中最好想的吧。。)
一些tips:
-
如果求类似最大值最小,考虑和二分答案相结合,用最大流、可行流check等等
-
与源汇点、二分图有关三大套路:格子染色(用于仅与相邻有关的)、数学分奇偶性(包括二进制分组)、矩阵分横纵以点连线
-
拆点,每个状态为一个点或入边->出边,中间是限制条件。点数太大了考虑动态加点。
-
任意两边的交点都在顶点上的图称为平面图,如果我们把面作为点,相邻的边连线,可以得到对偶图,对于数据点过大的,平面图最小割=对偶图最短路。
-
分数规划,其实就是把分母乘过去,然后二分验证。
-
对于平方的处理:拆边,假设全一种情况,考虑增量;或根据2k+1来连。
-
对于:最多x个满足什么条件,可转化为至少总数-x个满足非这个条件
-
二分图上跑最大流的复杂度是 \(O(m\sqrt{n})\)
·如果不刻意卡,6e3-1e5的点数甚至都能过去!网络流就是要敢写!!!
模拟费用流
神秘算法,本质是贪心。大概就是如果数据范围比较大网络流跑不过去,且有一定特殊性质时可以使用。
如 [NOI2019] 序列
我们先考虑“自由流”,即这么流一定不会使答案更劣的流,流满它。然后考虑流其他流,注意模拟退流等等。用优先队列维护。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号