P11363 [NOIP2024] 树的遍历 解题报告

P11363 [NOIP2024] 树的遍历解题报告

前言：

我以前没写过容斥的题，更别说树上容斥了。此处通过阅读题解学会的，特此记录。

理解题目:

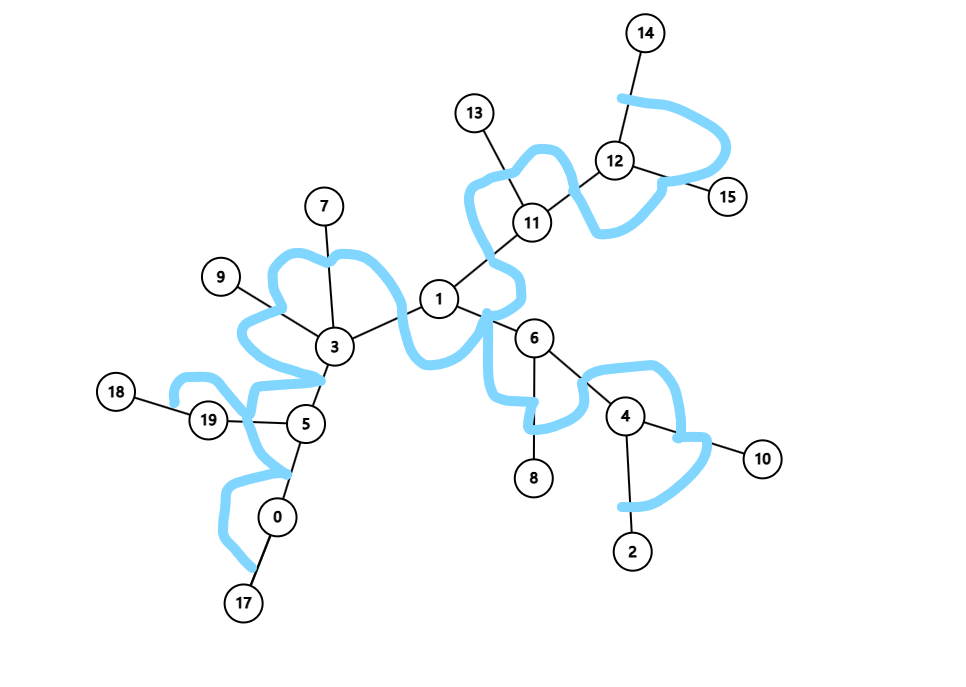
那些蓝色的就是树的遍历，我们可以观察到，树的遍历后是一个树，（重要性质）并且对于一个节点，环绕在他与他子节点之间边上的遍历方法决定了这种环绕是一条链，然后链有两个端点。

思路：

首先有部分分，\(k=1\)，链，菊花啥的，此文不管。

书接上回，我们发现每个节点（单独考察节点 \(u\)）与子节点的边上的图是环绕链，链上的每个边节点（乱讲的，这里表示遍历到的边当作节点看待，并加以区分）有以下的连接特征：

1. 环绕链的两个端点受要向外连出 这个条件控制，因而当确定两端之后，\(u\) 做出了贡献 \((degree[u]-2)!=(degree[u]-1)!\times(degree[u]-1)^{-1}\)
2. 考察\(u\) 下的边节点，不能同时有超过 \(2\) 条钦定的边节点（或可能的做为根的边节点）（自然做为端点，因而确定了环绕链）
3. 若 \(u\) 下没有钦定的边节点，他的贡献为 \((degree[u]-1)!\)
4. 综合一下，若是一棵边节点构成的树确定，其上可能的根节点（里面可以包含钦定的和不钦定的，但一定可能做为根节点）连起来必然构成一条全树上的链。

我们可以通过计算同一条根组成的链上的树的数，我们对每个节点进行贡献的清算，此处把 \(\sum (degree-1)!\) 提出，后面乘的东西做为贡献/权值。清算涉及此处的点下是否有钦定，以及是否算重复的问题。此处用容斥：

​ 设钦定的变集为 \(S\)，g[S] 为同时能以他们为根边节点的方案数，则方案总数为 \(\sum_{S}(-1)^{|s|+1}g(S)\)。此处注意非钦定边影响答案的清算（但是不影响非钦定边的数量）。

我们树上计数，设计状态 f[u] 为 \(u\) 子树恰好存在一个环绕链的端点 的贡献，记 \(c_u\) 为当前节点贡献后面乘的东西。

当当前点 \(u\) 下有钦定边（可以作为某一个端点）时：

​ 只选 \(u\)；只选子树中的链；两个都选。注意只选一个时贡献负的，多选一个多带一个负号。

\[f_u=-1+c_u\sum_{v\in son(u)}f_v-c_u\sum_{v\in son(u)}f_v=-1 \]

当当前点下无钦定边（不可以做为某个端点）时：

​ 只能选子树的链；

\[f_u=c_u\sum_{v\in son(u)}f_v \]

如何计算答案？

考察每一个节点 \(u\)，若可以做为一个端点，可以向下连，先贡献 \(1\)（只选自己），当前链贡献和为 \(-1\)（还没乘-1，即次数上的+1未处理），他下的环绕链必然有两个端点，我们考虑枚举这两个端点（记作 \(a,b\)），但是复杂度不对，我们前缀和:

​ 要计算 \(-c_u\sum_{a\ before\ b}f_a\times f_b\)，枚举 \(v\)，令 \(s=\sum_{a\ before\ b}f_a\)。

然后就好了，我大概知道到这种程度。

注意逆元，别似那了。P3811 【模板】模意义下的乘法逆元 - 洛谷

code:

#include<bits/stdc++.h>
using namespace std;
#define _int __int128
#define pii pair<int,int>
#define fi first
#define se second
#define ll long long
const int mod=1e9+7,maxn=1e5;
int n,k,vs[maxn+10];
_int fac[maxn+10],inv[maxn+10],ans=0,f[maxn+10];
vector<pii>g[maxn+10];
void init(){
	fac[0]=inv[0]=fac[1]=inv[1]=1;
	for(int i=2;i<=maxn;++i)fac[i]=fac[i-1]*i%mod,inv[i] = (mod-mod/i)*inv[mod % i]%mod;
}
_int M(_int x){
	return (x%mod+mod)%mod;
}
void dfs(int u,int fa,int op){
	_int s=-op,cu=inv[g[u].size()-1];
	ans+=op,f[u]=-op;
	for(auto o:g[u]){
		int v=o.fi,i=o.se;
		if(v==fa)continue;
		dfs(v,u,vs[i]);
		ans-=cu*s%mod*f[v]%mod;
		f[u]+=(op?0:f[v])*cu%mod;
		s+=f[v];
		s=M(s);
		f[u]=M(f[u]);
		ans=M(ans);
	}
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0);
//	freopen("traverse.in", "r", stdin);
//	freopen("traverse.out", "w", stdout);
	int c,t;cin>>c>>t;
	init();
	while(t--){ 
		cin>>n>>k;
		for(ll i=1,u,v;i<n;++i){
			cin>>u>>v;
			g[u].push_back({v,i});
			g[v].push_back({u,i});
		}
		for(int i=1,e;i<=k;++i){
			cin>>e;
			vs[e]=1;
		}
		dfs(1,0,0);
		for(int i=1;i<=n;++i)ans=M(ans*fac[g[i].size()-1]%mod);
		cout<<(ll)ans<<"\n";
		ans=0;
		for(int i=1;i<=n;++i){
			vs[i]=0;
			g[i].clear();
		}
	}
	return 0;
}