数据预处理--噪声数据处理、数据不一致处理、数据合并

1  噪声数据处理

噪声时一个测量变量中的随机错误或偏差，包括错误值或偏离期望的孤立点值，在R中可以调用outliers软件包中的outlier（）函数寻找噪声点，该函数通过寻找数据集中于其他观测值及均值擦话剧很大的点作为异常值，函数的格式为：

 

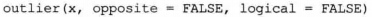
其中x表示一个数据，通常是一个向量，如果x是一个数据框或矩阵，则将逐列计算，opposit为T或F，若为T，给出相反值（如果最大值于均值差异最大，则给出最小值），logical为T或F，若为T，则给出逻辑值，把可能出现噪声的位置用TRUE表示。

#install.packages("outliers")

library(outliers)

set.seed(1234)

y<-rnorm(100)    #随机生成100个标准正太随机数

outlier(y)   #找出其中利群最远的值

 

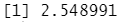
outlier(y,opposite = T)   #找出最远离群值相反的值

 

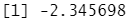
dotchart(y)     #绘制点图

 

dim(y)<-c(20,5)    #将y中的数据重新划分呈20行5列

outlier(y)   #求矩阵中每列的离群值  

 

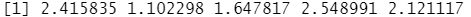
outlier(y,opposite = T)     #求矩阵中每列的离群值的相反值

 

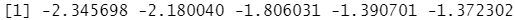
set.seed(1234)

y=rnorm(10)   #随机生成10个标准正态随机数

outlier(y,logical = T)   #返回相应逻辑值，离群点用TRUE标记

 

plot(y)   #绘制散点图

 

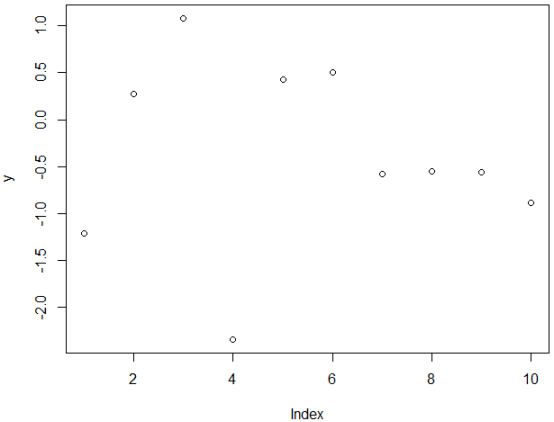
离群点话还可以通过聚类的方法进行检测，落在“簇”集合之外的值被视为离群点。

在进行噪声见检查后，操作实际中常用分箱、回归、计算检查和人工检查结合等方法光滑数据，去掉数据中的噪声。

分箱方法是通过对数据进行排序，利用数据“近邻”来光滑有序数据值的一种局部光滑方法。在分箱方法中，可以使用箱均值、箱中位数或箱边界等进行光滑。箱均值光滑、箱中位数光滑分别为对于每个“箱”，使用其均值或中位数来代替箱中的值；而箱边界光滑则是指将给定箱中的最大值和最小值被视为箱边界，箱中每一个值都被替换为最近边界。一般而言，宽度越大，光滑效果越明显。箱可以是等宽的，即每个箱的区间范围是常量。

下面以等宽均值光滑方法为例：

set.seed(1234)

x<-rnorm(12)

x<-sort(x)  #对x排序

dim(x)<-c(3,4)  #将数据形式转换成3行4列的矩阵，每行代表一个箱

x[1,]<-apply(x,1,mean)[1]   #用第1行的均值代替第1行中的数据

x[2,]<-apply(x,1,mean)[2]   #用第1行的均值代替第1行中的数据

x[3,]<-apply(x,1,mean)[3]   #用第1行的均值代替第1行中的数据

#apply()函数是通过对数组或矩阵的边际应用一个函数而获得的数值列表。x是一个向量或数组，MARGIN取值1表示行，2表示列。

 

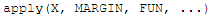
x

 

回归是指通过一个函数拟合来对数据进行光滑处理。线性回归涉及找出拟合两个变量的“最佳”直线，使得一个属性可以用来预测另一个;多元线性回归是线性回归的扩充，其中涉及的属性多于两个，并且数据拟合到一个多维曲面。

2 数据不一致的处理

当对数据进行批量操作时，可以通过对函数返回值进行约束，根据是否提示错误判断、是否存在数据不一致问题，如vapply函数。

vapply函数的作用是对一个列表或向量进行指定的函数操作，其常用格式如下:

 

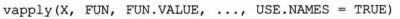
其中X是作为输入变量的列表或向量， FUN是指定函数， FUN.VALUE是函数要求的返回值,当USE.NAMES赋值为TRUE且X是字符型时，若返回值没有变量名则用X作为变量名。

x<-list(a=1:10,beta=exp(-3:3),logic=c(T,F,F,T))  #生成一个列表

x

 

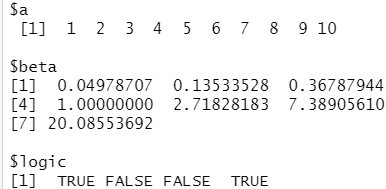
probs<-c(1:3/4)   #设置返回3个数

rt.value<-c(0,0,0)   #设置返回值为3个数字

vapply(x,quantile,FUN.VALUE = rt.value,probs=probs)

 

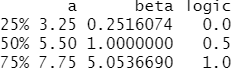
probs<-c(1:4/4)    #设置返回4个数

rt.value<-c(0,0,0,"")    #设置返回3个数和1个字符串

vapply(x,quantile,FUN.VALUE = rt.value,probs=probs)

由于要求返回值的种类必须是'character'，但 FUN(X[[1]I)结果的种类却是'double'，导致产生错误提示。

因此可以根据vapply函数的这一功能，使用FUN.VALUE参数对数据进行批量检测。

3 数据合并（集成）

 

数据集成是指将多个数据源中的数据合并，并存放到一个一致的数据存储(如数据仓库)中。这些数据源可能包括多个数据库、数据立方体或一般文件。

 

冗余是数据集成的另一个重要问题。两个数据集有两个命名不同但实际数据相同的属性，那么其中一个属性就是冗余的。另外，一个属性若可以通过另一个属性的一定变换得出，那么其中一个属性就可能是冗余的。

 

可以用相关分析对数据集冗余进行检测。给定两个属性，这种分析可以根据可用的数据，度量一个属性能在多大程度上包含另一个。对于定性数据，可以使用卡方检验。对于定量数据，我们使用相关系数和协方差，它们都能评估一个属性的值如何随另一个变化。若两个属性之间存在较大的相关系数，则其中一个可以被视作冗余而删除。

 

x<-cbind(sample(c(1:50),10),sample(c(1:50),10))  #生成有两列不相关的定性数据组成的矩阵

 

 

chisq.test(x)  #对矩阵x进行卡方检验，检验两列是否相关

 

 

 

结果分析：上述定性数据卡方检验结果显示，p-value<0.05，即在0.05显著性水平下拒绝相关的原假设，即变量不相关。

 

协方差为正，表示两个属性趋向于一起改变，即一个属性的某个观测值如果大于期望，则另一个属性的对应观测值很可能大于其期望。协方差为负，则表示两个属性趋向于相反方向改变。

 

x<-cbind(rnorm(10),rnorm(10))

 

cor(x)  #计算两列数据的相关系数

 

 

 

cov(x)   #计算两列数据的协方差

 

 

 

结果分析：由上述结果可以看出，两列数据的相关系数为0.4.23806，可以认为相关系数较小，两列之间的相关性不足以将两列数据视为冗余数据，无须删除。从协方差结果可以看出，两列协方差为正，两列趋于一同改变。

 

除了检测属性间的冗余外，还应该检测观测值是否存在重复。

 

x<-cbind(sample(c(1:10),10,replace = F),rnorm(10),rnorm(10))

 

#随机生成数据集，其中第1列为样本编号，若样本编号相同则认为存在重复  

 

head(x)   #去掉重复值前的若干观测值

 

 

 

y<-unique(x[,1])    #去掉重读样本编号

 

sub<-rep(0,length(y))    #生成列向量备用

 

for(i in 1:length(y)){        #循环根据样本编号筛选数据集，去掉重复观测值

 

  sub[i]<-which(x[,1]==y[i])[1]

 

}

 

x<-x[sub,]   

 

head(x)   #去掉重复观测值后的数据集