Padding、卷积步长（Strided convolutions）

 1 Padding

为了构建深度神经网络，需要学会使用的一个基本的卷积操作就是 padding，那么它是如何工作的呢？

上一节的例题可以看到，如果你用一个 3×3 的过滤器卷积一个 6×6 的图像，你最后会得到一个 4×4 的输出，也就是一个 4×4 矩阵。那是因为你的 3×3 过滤器在 6×6 矩阵中，只可能有 4×4 种可能的位置。这背后的数学解释是，如果我们有一个n × n的图像，用f × f的过滤器做卷积，那么输出的维度就是(n − f + 1) × (n − f + 1)。在这个例子里是6 − 3 + 1 = 4，因此得到了一个 4×4 的输出。这样的话会有两个缺点，第一个缺点是每次做卷积操作，你的图像就会缩小，从 6×6 缩小到 4×4，你可能做了几次之后，你的图像就会变得很小了，可能会缩小到只有 1×1 的大小，你可不想让你的图像在每次识别边缘或其他特征时都缩小，这就是第一个缺点，第二个缺点时，如果你注意角落边缘的像素，这些像素点只被一个输出所触碰或者使用，因为它位于这个 3×3 的区域的一角，如果是在中间的像素点，就会有许多 3×3 的区域与之重叠，所以那些在角落或者边缘区域的像素点在输出中采用较少，意味着你丢掉了图像边缘位置的许多信息。

为了解决这些问题，你可以在卷积操作之前填充这幅图像。在这个案例中，你可以沿着图像边缘再填充一层像素。如果你这样操作了，那么 6×6 的图像就被你填充成了一个 8×8 的图像。如果你用 3×3 的图像对这个 8×8 的图像卷积，你得到的输出就不是 4×4 的，而是 6×6的图像。习惯上，你可以用 0 去填充，如果p是填充的数量，在这个案例中，p = 1，因为我们在周围都填充了一个像素点，输出也就变成了(n + 2p − f + 1) × (n + 2p − f + 1)，所以就变成了(6 + 2 × 1 − 3 + 1) × (6 + 2 × 1 −3 + 1) = 6 × 6，和输入的图像一样大，这样一来，丢失信息或者更准确来说角落或图像边缘的信息发挥的作用较小的这一缺点就被削弱了。

至于选择填充多少像素，通常有两个选择，分别叫做 Valid 卷积和 Same 卷积，Valid 卷积意味着不填充，这样的话，如果你有一个n × n的图像，用一个f × f的过滤器卷积，它将会给你一个(n − f + 1) × (n − f + 1)维的输出。这类似于我们在前面的视频中展示的例子，有一个 6×6 的图像，通过一个 3×3 的过滤器，得到一个 4×4 的输出。另一个经常被用到的填充方法叫做 Same 卷积，那意味你填充后，你的输出大小和输入大小是一样的。根据这个公式n − f + 1，当你填充p个像素点，n就变成了n + 2p，最后公式变为n + 2p − f + 1。因此如果你有一个n × n的图像，用p个像素填充边缘，输出的大小就是这样的(n + 2p − f + 1) × (n + 2p − f + 1)。如果你想让n + 2p − f + 1 = n的话，使得输出和输入大小相等，如果你用这个等式求解p，那么p = (f − 1)/2。所以当f是一个奇数的时候，只要选择相应的填充尺寸，你就能确保得到和输入相同尺寸的输出，只有f是奇数的情况下，Same 卷积才会有自然的填充。以上就是如何使用padding卷积。

 2  卷积步长（Strided convolutions）

卷积中的步幅是另一个构建卷积神经网络的基本操作，下面是一个例子。和之前不同的是，我们把步幅设置成了2，你还和之前一样取左上方的 3×3 区域的元素的乘积，再加起来，以下这张图片很好好的说明了步长为2是如何进行卷积操作：

 

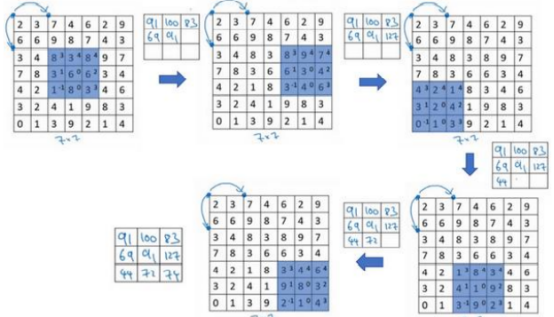
所以在这个例子中，我们用 3×3 的矩阵卷积一个 7×7 的矩阵，得到一个 3×3 的输出。如果你用一个f × f的过滤器卷积一个n × n的图像，你的 padding 为p，步幅为s，在这个例子中s = 2，你会得到一个输出，因为现在你不是一次移动一个步子，而是一次移动s个步子，输出于是变为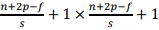：。如果商不是一个整数怎么办？在这种情况下，我们向下取整。⌊ ⌋这是向下取整的符号，这也叫做对z进行地板除(floor)，这意味着z向下取整到最近的整数，这个原则实现的方式是，你只在蓝框完全包括在图像或填充完的图像内部时，才对它进行运算，如果有任意一个蓝框移动到了外面，那你就不要进行相乘操作，这是一个惯例。

在进行卷积计算之前，会把将 3×3 的过滤器沿水平和垂直轴翻转，这相当于将 3×3 的过滤器做了个镜像，然后进行卷积运算，我们在定义卷积运算时，跳过了这个镜像操作。从技术上讲，我们实际上做的，我们在前面视频中使用的操作，有时被称为互相关（cross-correlation）而不是卷积（convolution）。但在深度学习文献中，按照惯例，我们将这（不进行翻转操作）叫做卷积操作。