重链剖分
阅读这篇文章前,你必须要十分熟悉线段树的各种操作。
我不会做ppt/ll
先来看一棵树:
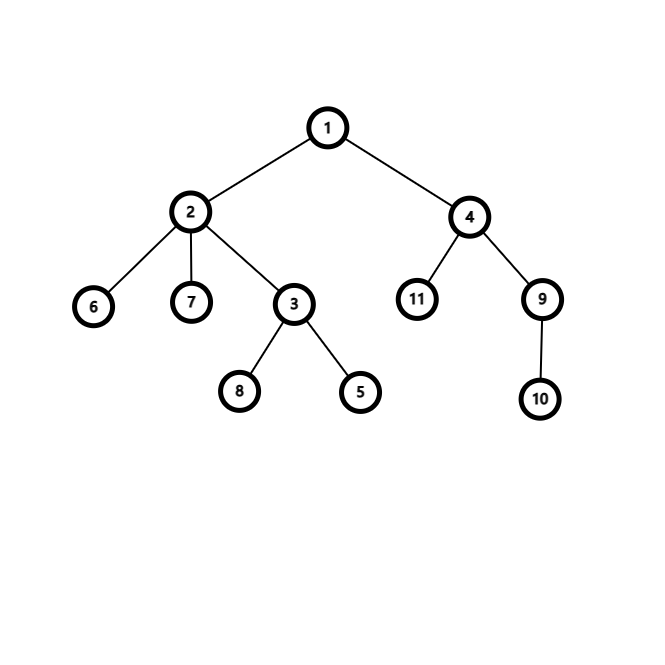
树剖的经典问题:
两种操作,一种是将点 \(u\) 到点 \(v\) 路径上所有点加上一个值;第二种是查询路径 \(u\) 到路径 \(v\) 的点权之和。
显然,普通的树上差分已经无法解决这种问题了。
于是我们需要一种预处理来降低复杂度。
区间修改,这肯定用到线段树,但是这是一棵树,我们如何把他变成连续区间呢。
于是树剖诞生了:我们将整棵树按照重儿子(一个节点的儿子中,以其为根的子树大小是所有儿子中最大的,他就是重儿子)优先遍历,按遍历顺序将每个点打上一个序号(这就是 dfn 序)(不是重儿子的结点遍历顺序随便,如果有子树大小相同的儿子,任选一点作为重儿子),于是整棵树变成了:
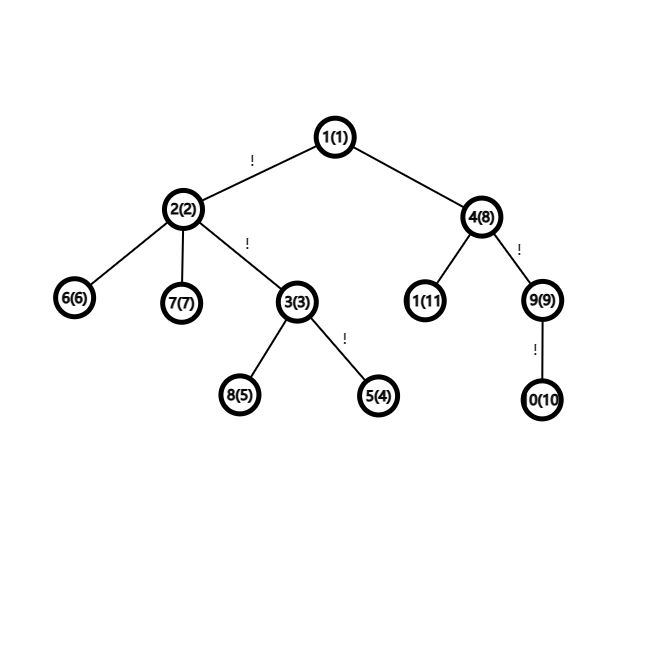
所有点旁边括号内就是我给这个点标上的 dfn 序,所有与重子的连边我都打上了感叹号。
你会发现,感叹号形成了一个个链(我们称之为重链),这棵树就可以抽象成:
是挺抽象的
有意思的是一条重链上所有点的 dfn 序是连续的,于是我们就可以把这一整棵树改成一个个区间了!
然后就可以用线段树维护重链了,每次查询完,就跳一次父亲进入另一条重链。
至于复杂度证明,我们发现每查询一次重链,是 \(\log{n}\) 的,复杂度就在于我们会跳父亲,但是每跳一次父亲,子树大小就会至少翻倍,所以最多跳 \(\log{n}\) 次父亲,于是复杂度最多就是 \(\log^2{n}\)。
至于查询一个点以其为根的子树中所有点的点权的和(或者最值)这种问题,你会发现,子树中的 dfn 序是连续的,所以只用在线段树上求该点的 dfn 序到该点 dfn 序加上该子树大小再减一的区间即可。
具体讲一下实现:
先进行一次 DFS 处理出重子,深度,子树大小,每个点的父亲。
然后再进行一次 DFS 求出该点表上的序号、所在的重链的链首(就是深度最小的那个,也是序号最小的那个)即可(记得要先遍历重子,再遍历轻儿子)。
修改和查询时,两边的两个点优先跳深度大的那个,如果发现两点在同一条链上,就结束,然后修改这两个点之间的点即可(区间修改嘛,都会吧)。
线段树的实现我还讲吗……
很简单,是吧
然后上好题:
送的。
还是送的。
相信简单的边权转点权都会吧。
由于每个点只有一个父亲(【数据删除】?),所以我们把每个点到他父亲的边的边权存在这个点上就可以了(根节点为点权零哦)。
相信简单的边权转点权都会吧。
好极了,又是一道边权转点权。
只能我无语了。
好啊好啊,妙极了
再来。
啥呀这,蚌。
应该,没了?(?)
上点硬菜:
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
我们每次将修改的路径上的每一个点都染上一个不相同的颜色,如果一条边所连接的两个点同色,这条边就是重边,否则就是轻边。
然后线段树可以维护这个东西,一个区间只需记录左端的颜色,右端的颜色以及区间内的重边数量(我把区间包装成了结构体)。合并的时候就是如果左区间右端点和右区间左端点颜色相同,则答案还需要加一。
注意询问的时候往上跳的时候两边要维护两个结构体,跳哪边就往哪边合并,最后再一起合并。
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
和上题一样,记录一个左端点颜色、右端点颜色、区间内颜色段个数。
每次合并的时候如果左半边右端点颜色如果等于右半边左端点颜色,颜色段数量就减一。
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
常用套路:删可以离线下来改为加。
先把删完的图整出来,然后从这个图中整一棵树出来(你直接 DFS 找或者什么别的都行,我是 DFS 记录了每个点的父亲整出这棵树)。
可以发现,我们可以把一开始整棵树所有边全都标上 1 表示关键边。
然后我们把多余的边加进去,就把这条边所连的两个点之间的路径设为 0 即可。
剩下的树剖裸题。
P5838 [USACO19DEC]Milk Visits G
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
树剖+经典的区间颜色查询。
vector记录每个颜色所在位置,排好序,找到对应区间直接二分找有没有就行了。
鬼畜可爱萌萌题欸。
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
\(\textcolor{white}{ }\)
染的色互不相同,于是我们可以计算颜色段数量,但发现不好维护询问 \(1\)。
转换思路,我们线段树直接维护最大值(从这个点到根节点上的颜色数量),在每次修改的时候直接区间修改最大值
容易发现这东西有可加减性,所以链的询问就变成了 \(val_u+val_v-2 \times val_{lca(u,v)}+1\)
考虑每次修改一条链后会发生什么。
我们发现修改对于不同颜色在这条路径上的链上的点的效果是不一样的。
所以我们可以暴力的维护颜色段的起始段和终止段,然后就可以暴力计算出该颜色在修改路径上的链的起始点和终止点,暴力修改。对于这个颜色链的链首,我们求算出链首到根的颜色段数量,将以链首为根的整棵子树减去这个值再加一,然后再给上一个修改过的颜色链加回来。考虑到每个点被修改过这个点到根的颜色会被覆盖成一种颜色,于是可以发现时间复杂度是正确的(感性理解吧,不是很容易说清楚,如果有人有严格证明,可以私信我)。
last update at:2023-05-30 22:40:40 星期二


 浙公网安备 33010602011771号
浙公网安备 33010602011771号