平衡树好题

前言

基础实现我是真的不想讲了，都讲烂了，如果不会团队文件下载某人的平衡树ppt自学吧挺清楚的。

这里主要讲题。

需要学的就只有 splay 和 fhq_treap。

splay 狗都不学，fhq_treap yyds！ --xeqwq

我觉得我也不会写的比神仙ty更好了，所以就用他的吧。

有些题都讲烂了（例如NOI2005的某道题），这里换了一堆我新发现的题。

好题

~~好题太多了，把基础实现给挤掉了。~~

我们是北京人，就要用北京人发明的东西，所以今天所有题目都是可以用 fhq_treap 做的，splay弃掉，常数大还难写的东西！

范浩强是神！

文艺平衡树

你只需要反转时把他分裂出来打上标记即可。

splay是什么，有 fhq_treap 好写吗？

P4036 [JSOI2008]火星人

第一行给出初始的字符串。第二行是一个非负整数 \(M\) ，表示操作的个数。接下来的M行，每行描述一个操作。操作有 \(3\) 种，如下所示

询问。语法：\(Q\) \(x\) \(y\) ，\(x\) ,\(y\) 均为正整数。功能：计算 \(LCQ(x,y)\) 限制：\(1\) \(\leq\) \(x\) , \(y\) \(\leq\) 当前字符串长度。
修改。语法：\(R\) \(x\) \(d\)，\(x\) 是正整数，\(d\) 是字符。功能：将字符串中第 \(x\) 个数修改为字符 \(d\) 。限制：\(x\) 不超过当前字符串长度。
插入：语法：\(I\) \(x\) \(d\) ，\(x\) 是非负整数，\(d\) 是字符。功能：在字符串第 \(x\) 个字符之后插入字符 \(d\) ，如果 \(x=0\)，则在字符串开头插入。限制：\(x\) 不超过当前字符串长度

LCQ：后缀之间的最长公共前缀

蛤，后缀之间的最长公共前缀

蛤，这不后缀数组吗？

蛤？还有修改？？？？

\(\text{ }\)

TIP 1:

哈希二分比较

\(\text{ }\)

TIP 2:

既然带有插入，带有插入+修改，能不能用平衡树捏？

\(\text{ }\)

TIP 3 区间hash的求法：

设 \(\text{hash}\) 值为 \(p\)。

来自 P3167 [CQOI2014]通配符匹配的方法：

对于 \(l\) 到 \(r\) 的字串，其哈希值为：\(hash_r-hash_l\times p^{r-l}\)

对于 \(p\) 的幂，我们可以预处理，于是可以做到 \(O(1)\) 求。

\(\text{ }\)

解法

显然有模数不好处理，所以我自然溢出了。

正常的 fhq_hteap 处理序列的区间查询等问题就行了。

然后放一个 pushup 的代码：

void pushup(int i)
{ 
    t[i].sz=t[lson].sz+t[rson].sz+1;
    t[i].hs=t[rson].hs+t[lson].hs*power[t[rson].sz+1]+t[i].val*power[t[rson].sz];
}

应该很容易明白吧。

P2161[SHOI2009]会场预约

你需要维护一个在数轴上的线段的集合 \(S\)，支持两种操作：

A l r 表示将 \(S\) 中所有与线段 \([l,r]\) 相交的线段删去，并将 \([l,r]\) 加入 \(S\) 中。

B 查询 \(S\) 中的元素数量。

对于 A 操作，每次还需输出删掉的元素个数。

\(\text{ }\)

解法

struct sg
{
	int l,r;
	bool operator < (const sg x) const
	{
		return r<x.l;
	}
};

是不是一看就懂了？

这样的话可以保证如果两个线段相交必然在 set 中是相等的。

然后再用 set 暴力删除就行了。

复杂度易证是正确的。

P3165 [CQOI2014]排序机械臂

为了把工厂中高低不等的物品按从低到高排好序，工程师发明了一种排序机械臂。它遵循一个简单的排序规则，第一次操作找到高度最低的物品的位置 \(P_1\) ，并把左起第一个物品至 \(P_1\) 间的物品 (即区间 \([1,P_1]\) 间的物品) 反序；第二次找到第二低的物品的位置 \(P_2\) ，并把左起第二个至 \(P_2\) 间的物品 (即区间 \([2,P_2]\) 间的物品) 反序……最终所有的物品都会被排好序。

样例说明

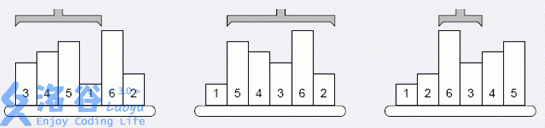
上图给出有六个物品的示例，第一次操作前，高度最低的物品在位置 \(4\) ，于是把第一至第四的物品反序；第二次操作前，第二低的物品在位罝六，于是把第二至六的物品反序……

你的任务便是编写一个程序，确定一个操作序列，即每次操作前第 \(i\) 低的物品所在位置 \(P_i\) ，以便机械臂工作。需要注意的是，如果有高度相同的物品，必须保证排序后它们的相对位置关系与初始时相同。

\(\text{ }\)

由于都是在同一个序列中处理，所以我们可以预先存下每个数的编号，然后便特别好写了。

然后按照题目说的用 fhq_treap 反转就行了。

P1110 [ZJOI2007] 报表统计

在最开始的时候，有一个长度为 \(n\) 的整数序列 \(a\)，并且有以下三种操作：

INSERT i k：在原数列的第 \(i\) 个元素后面添加一个新元素 \(k\)；如果原数列的第 \(i\) 个元素已经添加了若干元素，则添加在这些元素的最后。
MIN_GAP：查询相邻两个元素的之间差值（绝对值）的最小值。
MIN_SORT_GAP：查询所有元素中最接近的两个元素的差值（绝对值）。

\(\text{ }\)

TIP：

发现每个原数组中的元素都可以看作为一个序列，然后我们在记录一下相邻两个序列的首元素与尾元素只差即可。

\(\text{ }\)

正解

想必都会了。

我们两个序列之间可以用一个 multiset 维护差值，每次更新删除原来的插入新的就行了。

总体差值最小只需要用一个 multiset 维护就行了，每次找到大于等于它最小的和小于他最大的就行了。

CF675D Tree Construction

给定一个有 \(n\) 个数组成的序列，在此基础上构建一棵二叉排序树，求每个节点（根节点除外）的父节点的编号是多少。

\(\text{ }\)

正解

每个点的父亲节点只能是他的前驱或者后继。

我们模拟一下插入的过程可以发现是较后插入的是父亲节点。

然后 set 维护即可。

P8099 [USACO22JAN] Minimizing Haybales P

Bessie 感到无聊，于是又在 Farmer John 的牛棚里制造麻烦。FJ 有 \(N\)（\(1 \le N \le 10^5\)) 堆草堆。对于每个 \(i \in [1,N]\)，第 \(i\) 堆草堆有 \(h_i\)（\(1 \le h_i \le 10^9\)）的草。Bessie 不想让任何的草倒下来，所以她唯一可以执行的操作为：

如果两个相邻的草堆的高度相差不超过 \(K\)（\(1 \le K \le 10^9\)），她可以交换这两堆草堆。

Bessie 在一系列这样的操作之后可以得到的的字典序最小的高度序列是什么？

\(\text{ }\)

正解

思路是将小的数尽量往前移。

对于第 \(i\) 个数，每次平衡树上二分找到最左边的大于第 \(i\) 个点的合法的值的位置然后放到这个位置前面即可。

易知这是正确的。

fhq_treap 完全可以胜任区间反转等操作。

posted @ 2023-02-03 15:57 Y2y7m 阅读(51) 评论(0) 收藏举报

刷新页面返回顶部

Y2y7m

平衡树好题

前言

好题

文艺平衡树

P4036 [JSOI2008]火星人

TIP 1:

TIP 2:

TIP 3 区间hash的求法：

解法

P2161[SHOI2009]会场预约

解法

P3165 [CQOI2014]排序机械臂

P1110 [ZJOI2007] 报表统计

TIP：

正解

CF675D Tree Construction

正解

P8099 [USACO22JAN] Minimizing Haybales P

正解

公告