图的连通性问题
ps:本人太菜了,强连通分量是最近才开始上手写题的,勿喷。
Part1:判断图是否联通
相信不用多说:dfs一遍或者并查集
如果你是普及选手:
dfs做法:
从任意一个点开始遍历整个图,如果所有点都被遍历一遍,就是联通的。
并查集:
把每个边的两个点并在一起,看看是否所有点被并到一个集合里了。
计算连通块也可以用以上方法解决。
Part2:强连通分量
①:
什么是强连通分量?
“有向图强连通分量:在有向图G中,如果两个顶点 \(v_i\),\(v_j\) 间(\(v_i\) \(\neq\) \(v_j\))有一条从 \(v_i\) 到 \(v_j\) 的有向路径,同时还有一条从 \(v_j\) 到 \(v_i\) 的有向路径,则称两个顶点强连通 \((strongly\) \(connected)\)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量 \((strongly\) \(connected\) \(components)\)。”
说的通俗易懂一些:
一张有向图,其中有一个子图,这个子图需要满足:图中任意两点 \(v_i\), \(v_j\) (\(v_i\neq v_j\)),有一条路径可以从 \(v_i→v_j\),还有一条路径可以从 \(v_i←v_j\)。
强连通分量就是这张图中满足需求且最大的子图。
②:
如何求取强连通分量?
DFS
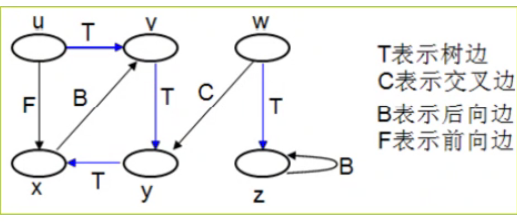
可能会出现以下四种边:
1.树边:DFS森林中某棵树上的边。
2.后向边:由森林中某棵树上的一个结点指向其祖先结点的点(又被称为返祖边)。
3.前向边:由森林中某棵树上的一个结点指向其后代结点的边(一般来讲删除这种边以后并不会影响结果)。
4.交叉边:是在两个不构成“祖先—后代”关系的结点之间的边(又称横插边)。
接下来引入两个数组:
\(dfn\) 数组以及 \(low\) 数组
\(dfn\) 就是 \(dfs\) 序,\(dfn[i]\) 记录的是顶点 \(i\) 第几个被遍历。
\(low\) 数组表示的是每个点能回到的 \(dfn\) 序最小的结点是哪个。
\(dfn\) 和 \(low\) 数组需要用 \(dfs\) 来求取.
在计算 \(dfn\) 和 \(low\) 的同时,我们也要用栈来存储遍历的点,当某个点 \(dfn[x]==low[x]\) 时,把从这个点到栈顶的点全部取出,这就是一个强连通分量
这就是tarjan算法
代码:
const int maxn=1e4+10;
vector<int> edge[maxn];
int dfn[maxn],low[maxn];
int cnt;
int s[maxn],top;
bool instack[maxn];
int ans,scc[maxn];
void tarjan(int u)
{
s[++top]=u;//把这个点扔进栈
instack[u]=1;
dfn[u] =low[u] =++cnt;
for(int i=0;i<edge[u].size();i++)
{
int v=edge[u][i];
if(!dfn[v])
{ //如果下一个点没有被搜过,
tarjan(v);//继续搜
low[u]=min(low[u],low[v]);//更新low
}
else if(instack[v])
{ //如果下一个点已经被搜过,看他在不在栈里
low[u]=min(low[u],dfn[v]);//更新low
}
}
if(dfn[u]==low[u])
{
ans++;//答案++,第几个强连通分量
int v;
while(1)
{
v=s[top--];
scc[v]=ans; //打标记
instack[v]=0;//出栈
if(v==u)
break;
}
}
}
Part3:tarjan的其他应用
1.求割边割点
割边定义:在无向连通图 ,若删除边 \(u->v\) 后,原图变成了两个联通分量,则称这条边是⼀条割边。
割点定义:在无向连通图 上,若删除节点 \(u\) 和所有与其相连的边的集合 之后,原图变成了两个以上的连通分量,则称节点 \(u\) 是⼀个割点。
割点的求法:当我们遍历到一个点时,如果他不经过他的父亲边时,他的 \(low\) 的值要大于等于他父亲节点的 \(dfn\) ,这个点就是割点。
这里只放上割点的代码:
#include <bits/stdc++.h>
using namespace std;
vector<int> edge[20010];
int n,m;
int low[20010];
int dfn[20010];
bool vis[20010];
int cnt;
int ans[20010];
int c;
void dfs(int u,int root)
{
dfn[u]=++cnt;
low[u]=cnt;
int sz=0;
for(int i=0;i<edge[u].size();i++)
{
int v=edge[u][i];
if(!dfn[v])
{
dfs(v,root);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]&&u!=root)
ans[++c]=u;
if(u==root)
sz++;
}
low[u]=min(low[u],dfn[v]);
}
if(sz>1&&u==root)
ans[++c]=u;
}
int main()
{
cin>>n>>m;
int u,v;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
edge[u].push_back(v);
edge[v].push_back(u);
}
for(int i=1;i<=n;i++)
{
if(!dfn[i])
{
dfs(i,i);
}
}
sort(ans+1,ans+1+c);
int c1=0;
for(int i=1;i<=c;i++)
{
if(ans[i]!=ans[i-1])
c1++;
}
cout<<c1<<endl;
for(int i=1;i<=c;i++)
{
if(ans[i]!=ans[i-1])
printf("%d ",ans[i]);
}
printf("\n");
return 0;
}
求割边与求割点差不多,可以自己想一想。
2.缩点
将一整个联通分量缩成一个点之后跑拓扑排序
const int maxn=10000+10;
int n,m;
int a[maxn];
int bl[maxn],dfn[maxn],low[maxn];
bool instack[maxn];
int s[maxn],top;
int c;
vector<int> edge[maxn],tp[maxn];
void tarjan(int u)
{
low[u]=dfn[u]=++c;
s[++top]=u;instack[u]=1;
for(int i=0;i<edge[u].size();i++)
{
int v=edge[u][i];
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(instack[v])
low[u]=min(low[u],low[v]);
}
if(dfn[u]==low[u])
{
int v;
while(v=s[top--])
{
bl[v]=u;
instack[v]=0;
if(u==v)
break;
a[u]+=a[v];//缩起来
}
}
}
int cnt[maxn],dis[maxn];
int topo()
{
queue<int> q;
int tot=0;
for(int i=1;i<=n;i++)
if(bl[i]==i&&!cnt[i])
{
q.push(i);
dis[i]=a[i];
}
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=0;i<tp[u].size();i++)//tp数组记录的是强联通分量之间的连边情况
{
int v=tp[u][i];
dis[v]=max(dis[v],dis[u]+a[v]);
cnt[v]--;
if(cnt[v]==0)
q.push(v);
}
}
int ans=0;
for(int i=1;i<=n;i++)
ans=max(ans,dis[i]);
return ans;
}
下面是强联通分量之间连边的代码:
for(int i=1;i<=m;i++)
{
int u=bl[tmp[i].u],v=bl[tmp[i].v];
if(u!=v)
{
tp[u].push_back(v);
cnt[v]++;
}
}
3.点双/边双连通分量
点双连通:若对于一个无向图,其任意一个节点对于这个图本身而言都不是割点,则称其点双连通。也就是说,删除任意点及其相关边后,整个图仍然属于一个连通分量。
边双连通分量:边双连通分量没有割边。
边双联通分量:
void tarjan(int u,int fa)
{
dfn[u]=low[u]=++cnt;
for(int i=head[u];i;i=nxt[i])
{
int v=ver[i];
if(!dfn[v])
{
tarjan(v,i);
if(low[v]>dfn[u])//如果不经过他与他父亲的这条边,就无法回到dfn更小的点,那这条边就是割边
{
int tmp=1ll*u*100000000+1ll*v;//我这里用的是暴力map存储
cut[tmp]=1;
tmp=1ll*v*100000000+1ll*u;
cut[tmp]=1;
}
low[u]=min(low[u],low[v]);
}
else if(i!=(fa^1))
low[u]=min(low[u],dfn[v]);
}
}
int bl[maxn];
void dfs(int u)//dfs简单计算一下边双联通分量
{
bl[u]=c;
dcc[c].push_back(u);
for(int i=head[u];i;i=nxt[i])
{
int v=ver[i];
int tmp=1ll*u*100000000+1ll*v;
if(bl[v]||cut[tmp])
continue;
dfs(v);
}
}
点双:
void tarjan(int u)
{
dfn[u]=low[u]=++cnt;
s[++top]=u;
instack[u]=1;
int tmp=0;
for(int i=0;i<edge[u].size();i++)
{
int v=edge[u][i];
if(!dfn[v])
{
tmp++;
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])
{
c++;
while(s[top+1]!=v) dcc[c].push_back(s[top--]);
dcc[c].push_back(u);
}
}
else if(instack[u])
low[u]=min(low[u],dfn[v]);
}
if(root==u&&tmp==0)
dcc[++c].push_back(u);
}
Part4:好题
题目描述
由于外国间谍的大量渗入,国家安全正处于高度的危机之中。如果 A 间谍手中掌握着关于 B 间谍的犯罪证据,则称 A 可以揭发 B。有些间谍收受贿赂,只要给他们一定数量的美元,他们就愿意交出手中掌握的全部情报。所以,如果我们能够收买一些间谍的话,我们就可能控制间谍网中的每一分子。因为一旦我们逮捕了一个间谍,他手中掌握的情报都将归我们所有,这样就有可能逮捕新的间谍,掌握新的情报。
我们的反间谍机关提供了一份资料,包括所有已知的受贿的间谍,以及他们愿意收受的具体数额。同时我们还知道哪些间谍手中具体掌握了哪些间谍的资料。假设总共有 \(n\) 个间谍(\(n\) 不超过 \(3000\)),每个间谍分别用 \(1\) 到 \(3000\) 的整数来标识。
请根据这份资料,判断我们是否有可能控制全部的间谍,如果可以,求出我们所需要支付的最少资金。否则,输出不能被控制的一个间谍(要求编号最小)。
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
这就是一张有向图,我们把每一个强连通分量缩成一个点,然后看看这些强连通分量之间的互相连边的情况,记录每个入度为 \(0\) 的强连通分量,这些强连通分量必须要买下。
无解就是有至少一个间谍不能被贿赂也不能被揭发。
弱化版:P2002 消息扩散
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
题目描述
在宽广的非洲荒漠中,生活着一群勤劳勇敢的羊驼家族。被族人恭称为“先知”的Alpaca L. Sotomon是这个家族的领袖,外人也称其为“所驼门王”。所驼门王毕生致力于维护家族的安定与和谐,他曾亲自率军粉碎河蟹帝国主义的野蛮侵略,为族人立下赫赫战功。所驼门王一生财宝无数,但因其生性节俭低调,他将财宝埋藏在自己设计的地下宫殿里,这也是今天Henry Curtis故事的起点。Henry是一个爱财如命的贪婪家伙,而又非常聪明,他费尽心机谋划了这次盗窃行动,破解重重机关后来到这座地下宫殿前。
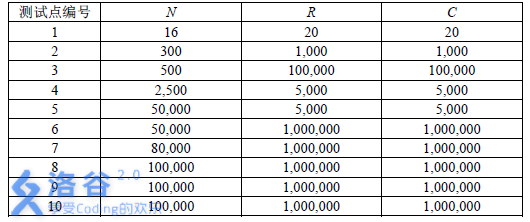
整座宫殿呈矩阵状,由R×C间矩形宫室组成,其中有N间宫室里埋藏着宝藏,称作藏宝宫室。宫殿里外、相邻宫室间都由坚硬的实体墙阻隔,由一间宫室到达另一间只能通过所驼门王独创的移动方式——传送门。所驼门王为这N间藏宝宫室每间都架设了一扇传送门,没有宝藏的宫室不设传送门,所有的宫室传送门分为三种:
-
“横天门”:由该门可以传送到同行的任一宫室;
-
“纵寰门”:由该门可以传送到同列的任一宫室;
-
“任意门”:由该门可以传送到以该门所在宫室为中心周围8格中任一宫室(如果目标宫室存在的话)。
深谋远虑的Henry当然事先就搞到了所驼门王当年的宫殿招标册,书册上详细记录了每扇传送门所属宫室及类型。而且,虽然宫殿内外相隔,但他自行准备了一种便携式传送门,可将自己传送到殿内任意一间宫室开始寻宝,并在任意一间宫室结束后传送出宫。整座宫殿只许进出一次,且便携门无法进行宫室之间的传送。不过好在宫室内传送门的使用没有次数限制,每间宫室也可以多次出入。
现在Henry已经打开了便携门,即将选择一间宫室进入。为得到尽多宝藏,他希望安排一条路线,使走过的不同藏宝宫室尽可能多。请你告诉Henry这条路线最多行经不同藏宝宫室的数目。
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
\(\text{ }\)
我们在每一行上建一个虚点,把横天边都连在这个点上;每列上建一个虚点,然后把每个纵寰边连在这个点上;任意门可以暴力连。
然后缩点跑拓扑即可


 浙公网安备 33010602011771号
浙公网安备 33010602011771号