YACS 2022年9月月赛 乙组 T1 区间交集（二） 题解

题目链接

错误的单调队列做法

刚看到这题我觉得是一个类单调队列做法。

先把输入的区间从左到右排序，然后把和第一个区间有交集的区间放到 $deque$ 里。

到第二个时就把前面不合法的删掉，后面如果有新的合法的，就把他放进去。

这样，每一轮结束时 $deque$ 的长度 $-1$ (自己不能和自己相交)就是这个和区间相交的区间个数了。

最后还要除以 $2$ ，因为 $a$ 和 $b$ 相交，那么 $b$ 和 $a$ 也会相交。

结果我一交，全错了，但是样例是全对的。。。

自信的代码：

#include <deque>
#include <iostream>
#include <algorithm>
using namespace std;
long long ans,tail = 1;
struct Node
{
    int l,r;
}a[300010];
bool cmp(Node n1,Node n2)
{
    return n1.l < n2.l || n1.l == n2.l && n1.r < n2.r;
}
int n;
deque<Node> d;
int main()
{
    cin >> n;
    for(int i = 1;i <= n;i ++) cin >> a[i].l >> a[i].r;
    sort(a + 1,a + n + 1,cmp);
    for(int i = 1;i <= n;i ++)
    {
        while(!d.empty() && d[0].r < a[i].l) d.pop_front();
        while(tail != n + 1 && a[tail].l <= a[i].r)
        {
            d.push_back(Node{a[tail].l,a[tail].r});
            tail ++;
        }
        ans += d.size() - 1;
    }
    cout << ans / 2 << endl;
    return 0;
}

找了半天一个错误样例都找不到，也分析不出来。

后来我用了 $rand$ 函数生成了长度为 $5$ 的序列，发现果然有问题啊！

这个做法的问题就在于他不会将后面不合法的删掉，除非把前面的全删完。

随便出一个不合法的数据：

3

1 5

2 2

3 3

在 $[1,5]$ 的回合时，他会把 $[2,2]$ 和 $[3,3]$ 都放进来，

在 $[2,2]$ 的回合时，他只会检查前面的 $[1,5]$ 是否符合要求而不会检查后面的 $[3,3]$ 能不能和自己相交导致多算。

所以，这种做法是错误的。

正解，二分

我们来想一想在排好序的区间集合中，和 $a$ 相交的区间集合 $b$。（假设 $a$ 是左边的区间）

$b$ 在排好序的区间集合中是不是连续的一段呢？

显然是，我们来看下和 $a$ 相交的区间满足什么要求：

假设这个区间是 $c$ ，那么 $a$ 的右端点一定要大于等于 $c$ 的左端点。

也就是说所有左端点小于等于 $a$ 的右端点并且大于等于 $a$ 的左端点的都可以。（为了不算重复，我们假设 $a$ 是左边的区间）

画个图，就是这样：

 

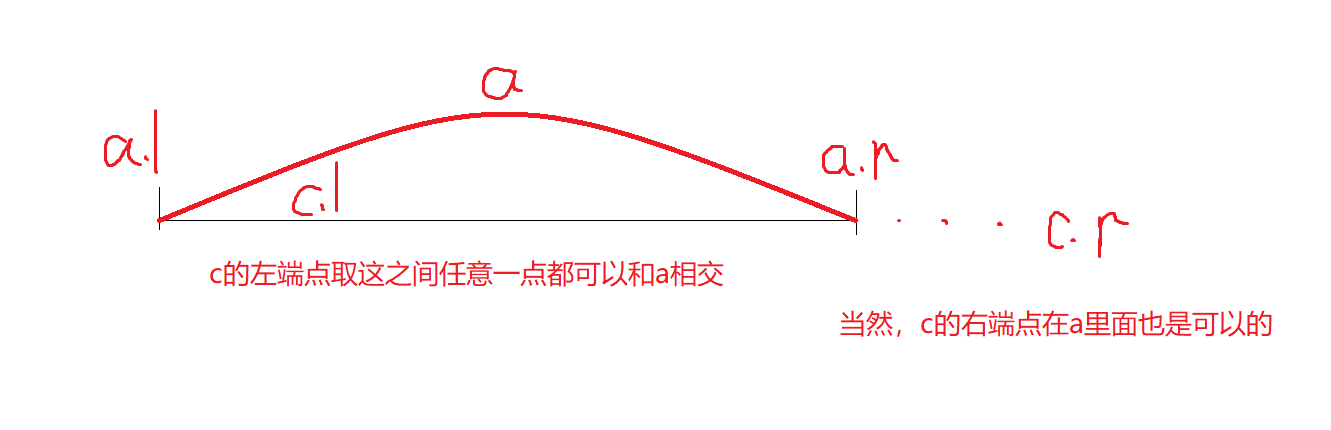
因为我们是把区间按照左端点排序的，所以我们可知：符合条件的区间一定是连续的一段。

那么，我们就可以二分他的右端点了。

那么，左端点是谁呢？

这个也好找，就是 $a$ 后面的第一个区间。

每次二分完右端点后，我们只需要拿他减掉 $a$ 的序号就可以得到和 $a$ 相交的区间个数了（ $a$ 是左边的区间），这样也不会算重。

最后需要注意下数据范围

十年心血一场空，不开 $longlong$ 见祖宗。

证明结束，该算法时间复杂度 $O(nlogn)$

展示一下代码：

#include <iostream>
#include <algorithm>
using namespace std;
#define int long long
int n,ans;
struct Sec
{
    int l,r;
}a[300010];
bool cmp(Sec s1,Sec s2)
{
    return s1.l < s2.l || s1.l == s2.l && s1.r < s2.r;
}
int check(int x)
{
    int l = 1,r = n,mid;
    int ret = n + 1;
    while(l <= r)
    {
        mid = l + r >> 1;
        if(a[mid].l > x)
        {
            ret = mid;
            r = mid - 1;
        }
        else l = mid + 1;
    }
    return ret;
}
signed main()
{
    cin >> n;
    for(int i = 1;i <= n;i ++) scanf("%d%d",&a[i].l,&a[i].r);
    sort(a + 1,a + n + 1,cmp);
    for(int i = 1;i <= n;i ++) ans += check(a[i].r) - i - 1;
    cout << ans << endl;
    return 0;
}