快速排序

---

快排思路：

1. 取第一个元素p，使元素p归位
2. 列表被p分成两部分，左边都比p小，右边都比p大
3. 递归完成排序

快排用到了分治的思想

分治算法就是把一个复杂的问题分成两个或更多的相同或类似的子问题，当子问题足够简单可以求出解的时候，把所有子问题的解合并起来，就可以得到原问题的解。

 

我们先搞定p归位的函数partition函数，然后左右两边的部分再去递归调用partition函数就得到最终目标了。

partition函数代码实现

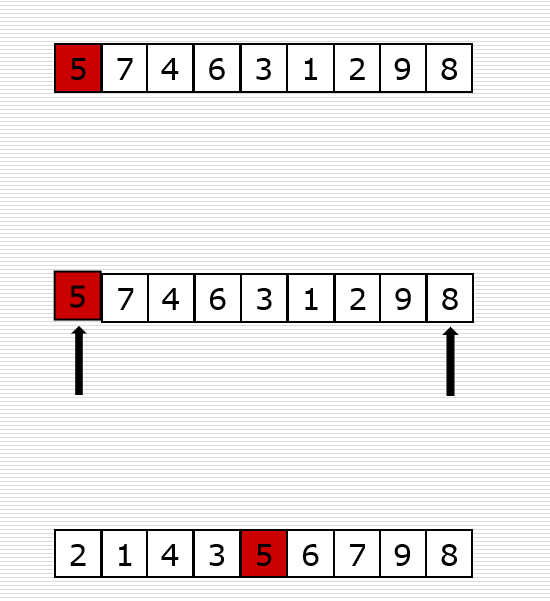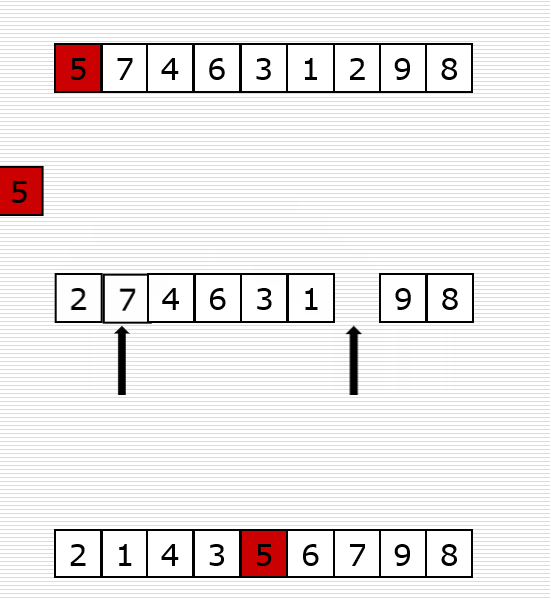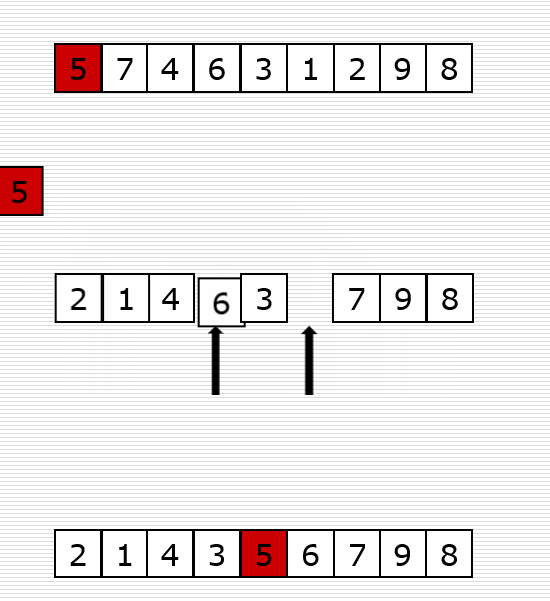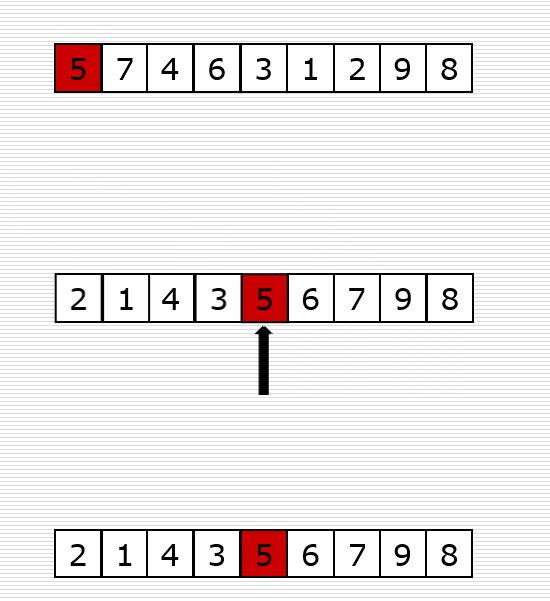
def partition(nums, left, right):
    # 从左边开始取数 进行归位（归位必须从右边开始，因为此时左边的第一个数拎出来了，所以左边有一个空位可以放数字）
    temp = nums[left]

    # 当left==right时，p回到中间的位置（此时左边全部数字都比p小，右边全部数字都比p大）
    while left < right:

        # 一开始是把左边第一个位置拎出来了，所以那个位置是空缺的，我们需要在右边找到一个比p值小的数填过来
        while left < right and nums[right] >= temp:
            right -= 1
        nums[left] = nums[right]

        # 到了这里的时候，右边就会有一个空缺位置，我们需要在左边找到一个比p值大的数填过来
        while left < right and nums[left] <= temp:
            left += 1
        nums[right] = nums[left]

    # 归位
    nums[left] = temp
    return left

 写完partition函数之后就可以把quick_sort函数写出来了（问题拆分）:

def quick_sort(nums, left, right):
    if left < right:
        mid = partition(nums, left, right)
        quick_sort(nums, left, mid - 1)
        quick_sort(nums, mid + 1, right)


if __name__ == '__main__':
    nums = list(range(100))
    import random
    random.shuffle(nums)
    quick_sort(nums, 0, len(nums) - 1)
    print(nums)

 小结：

1. 快排的时间复杂度为O（nlogn）
2. 用了递归，会有空间复杂度