2025-5-11 模拟赛

T1

银河帝国有 \(n\) 个国家，其中国家 \(1\) 是银河帝国的首都——川陀。国家之间有单向的星际轨道相连接（通过星际轨道穿越的时间均为单位时间），具体而言，对于国家 \(2\) 到国家 \(n\)，第 \(i\) 个国家恰好有一条从 \(i\) 到 \(p_i\) 的单向星际轨道（有 \(p_i<i\)），也就是说，通过星际轨道，任意一个国家均可抵达银河帝国的首都川陀，更进一步的，星际轨道使得银河帝国的交通形成了一棵根向树。

为应对银河系的所有可能的突发情况，每个国家有恰好一种特殊的能源储备，第 \(i\) 个国家的能源类型为 \(a_i\)，总共有至多 \(m\) 种类型的能源（不同国家可能有相同能源）。

接下来，银河帝国的川陀大学物理研究院向全银河系内所有国家发出最高学术指令，指令有 \(m\) 条，第 \(i\) 条指令形如，钦定 \(c\) 名研究人员，这 \(c\) 名人员分别来自银河帝国中 \(n\) 个国家中的一个（可能有人来自相同的国家），接下来 \(c\) 名人员将以最快速度在最短时间内通过单向星际轨道会合。在星际轨道穿越的过程中，研究人员可以选择采集经过的国家的能源样本（可以采集多个国家）。最终会合后研究人员将展开能源研究会议。

由于仪器适配等原因，川陀物理研究院要求：每名研究人员采集的能源样本互不相同；每名研究人员采集的能源样本数量相同；每名研究人员仅能采集经过的国家的能源样本。

对于每条指令，请你提前计算该会议总共最多可以采集的样本数量。由于指令的紧急性和机密性，每条指令对应的研究人员和会议均独立。

\(2\le n\le 300000,1\le m\le 1000,0\le q\le 50000,1\le p_i<i,1\le a_i\le m,2\le c\le 5\)。

时间限制 1 秒，空间限制 1024 MB。

sol

赛时不会，只写了 25 部分分。这题有一个直接 return 的 5pts 的部分分，防挂零。

翻译一下题面，这 \(c\) 个人走到的是这些点的最近公共祖先。
树上问题先考虑树剖，然后思考线段树维护什么。发现 \(m\) 比较小，所以在每个节点开一个 bitset 记录哪些能源种类存在，这样合并和查询的复杂度是 \(O(\frac{nm+qc\log(nm)}{\omega})\)。
现在我们有每个人能开的能源种类，然后就比较好算了。使用一些容斥，然后可以对于每个人员集合 \(S\) 得到能开的能源种类 \(dp_S\)（一个 bitset），复杂度 \(O(\frac{qm2^c}{\omega})\)，就可以算答案了。

设最终答案为 \(k\)，考虑构建⼀个⼆分图，左侧有 \(ck\) 个点（每名研究⼈员对应 \(k\) 个点），右侧有 \(m\) 个点（表⽰每⼀种类型的能源），连边表⽰对应研究⼈员可以开这种矿，则答案可⾏当且仅当该⼆分图有完美匹配。

接下来先引进一个定理：Hall 定理。
设二分图 \(G=<V_1,V_2,E>\) 中 \(|V_1|=m<=|V_2|=n\)，则 \(G\) 中存在从 \(V_1\) 到 \(V_2\) 的完全匹配当且仅当 \(V_1\) 中任意 \(k(k=1,2,\dots,m)\) 个顶点至少与 \(V_2\) 中 \(k\) 个顶点是相邻的。
证明可以去 csdn 上搜，这里不讲。

所以得到答案就是 \(k=\min{\frac{|dp_S|}{S}}\)，搞定。

T2

给定 \(m\) 个长度为 \(n\) 的排列，接下来进行如下操作：

初始序列 \(a\) 为空，每次取出任意一个排列中最靠前的数，加入到序列 \(a\) 的末尾，直到所有排列为空，如果结束时序列 \(a\) 中不存在连续 \(k\) 个相同的数，那么这个操作序列是好的。

定义 \(f(l,r)\) 表示仅考虑下标在 \([l,r](1\le l\le r\le m)\) 内的排列，当 \(k=r−l+1\) 时的好的操作序列的数量，注意相同的最终的序列 \(a\) 可能对应不同的操作序列。

计算 \(\sum_{i=1}^m\sum_{j=i}^m f(i,j)\) 对 \(998244353\) 取模。

\(2\le n,m\le 300\)，每一个输入的排列均在 \(n!\) 种排列中等概率随机生成。

时间限制 2 秒，空间限制 1024 MB。

sol

先容斥，再算数，再相信，赛时过了。

感觉想到容斥是明显的，先考虑 \(f(1,m)\)，枚举哪些元素连续出现了 \(m\) 次然后瞎容斥一下，每个情况的贡献可以组合数计算。

这个做法理论复杂度不知道，但是肯定极大。但是的但是我们不看理论复杂度，实际上这么做就过了，所以相信一下是很有用的。

然后我们考虑为什么相信。注意到哪些可以容斥，需要的是对于 \(l\sim r\) 这些排列，每一个的 \(i\) 都在 \(j\) 前面，估算一下发现概率是 \(\frac{1}{2^{r-l+1}}\)，非常小。所以直接处理出所有能容斥的序列组，相信一下就可以过了。

T3

平面上有 \(n\) 个整点，第 \(i\) 个整点的坐标是 \((x_i,y_i)\)。有 \(m\) 次询问，每次给定两个点 \((a_i,b_i)\) 和 \((c_i,d_i)\)，考虑以这两个点的连线作为对角线的正方形，判断该正方形的内部或边界上是否存在至少一个输入的整点。

\(1\le n,m\le 2\times 10^5,1\le x_i,y_i,a_i,b_i,c_i,d_i\le 10^8\)。

时间限制 4 秒，空间限制 1024 MB。

sol

赛时写了暴力分，多的没了。

kdt 和四分树被卡了（造数据人原话）

我们发现斜正方形很规范但又不是很规范（造数据人原话）所以我们考虑下面这坨分割

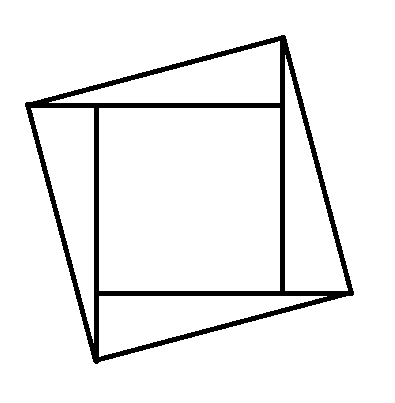
我们发现中间那一坨正方形很好处理，所以我们考虑剩下四个直角三角形。

发现我们只需要判断里面有没有点。考虑统⼀处理左边那个三⻆形：将所有点的纵轴坐标离散化，随后扫描线按照横轴坐标从左往右加⼊所有的点，当遇到平⾯中⼀个点的时候加⼊到纵轴维护的数据结构中，当遇到⼀个查询的三⻆形的直⻆顶点的时候，计算该直⻆三⻆形斜边的斜率，使⽤数据结构维护下凸包，取出纵轴区间，并使⽤该斜率去切该纵轴区间对应的凸包。将切凸包得到的决策点取出后判定其是否在直⻆三⻆形内部即可。

造数据人说这题应该还有一万种凸包做法，认为李超树能做，不过我不知道能不能，如果有大神做出来了请来吊打我/bx/bx

复杂度瓶颈是凸包上二分，总复杂度双 \(\log\)。