tabel
这里是大家喜闻乐见的中缀表达式树题解,没有后缀表达式解法的头疼问题~
说在最前面
一点小细节。
观察真值表可知,所谓 "蕴含词 → " 其实就是运算符 <=。所以一共的运算符集就是 !, &, |, <=, ==
然后,我们定义一个 "表达式" 形如:
(...) 或 !(...) 或 A 或 !A
其中 A 是某个简单命题。这样定义,好处就是原来的 ! 运算会被抹去,所有的 ! 都会被归纳成为某个表达式的 "属性"。在运算过程中,我们算出某个表达式内部的值是多少,之后如果该表达式具有 "取反的属性",我们再把答案取反之后返回
正题
我们将 ! 运算去除,事情就简单得多。现在运算符只剩下 &, |, <=, == 这几种,并且它们都是等优先级的。复杂度瓶颈就在于如何快速构建出表达式树。
考虑朴素递归建表达式树,对于当前要对区间 [l, r] 内的表达式建树,它有以下几种情况:
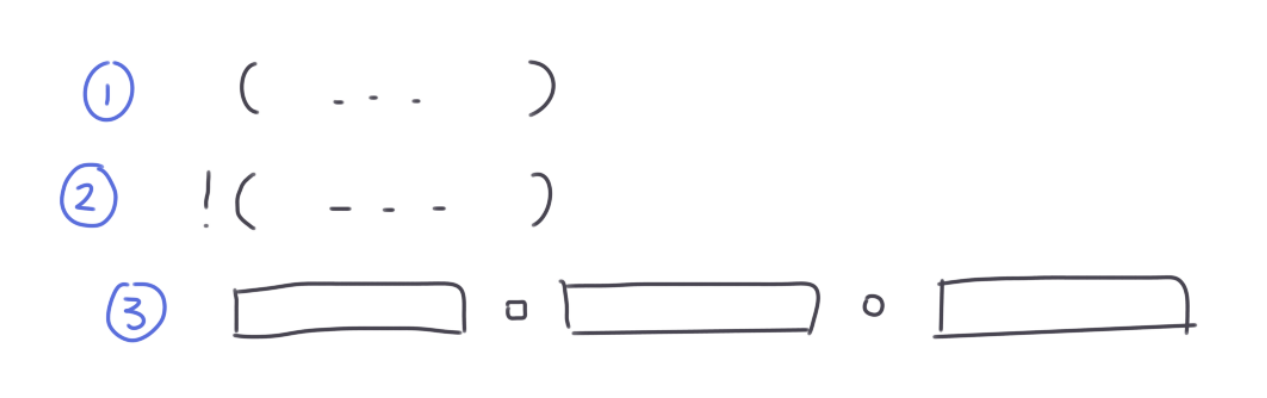
对于第一种情况,就是某式外面套了一层括号,那么对于这一层我们什么都不做,递归建立区间 [l + 1, r - 1]
对于第二种情况,我们标记 [l, r] 区间的表达式具有 "取反属性",递归建立区间 [l + 2, r - 1]
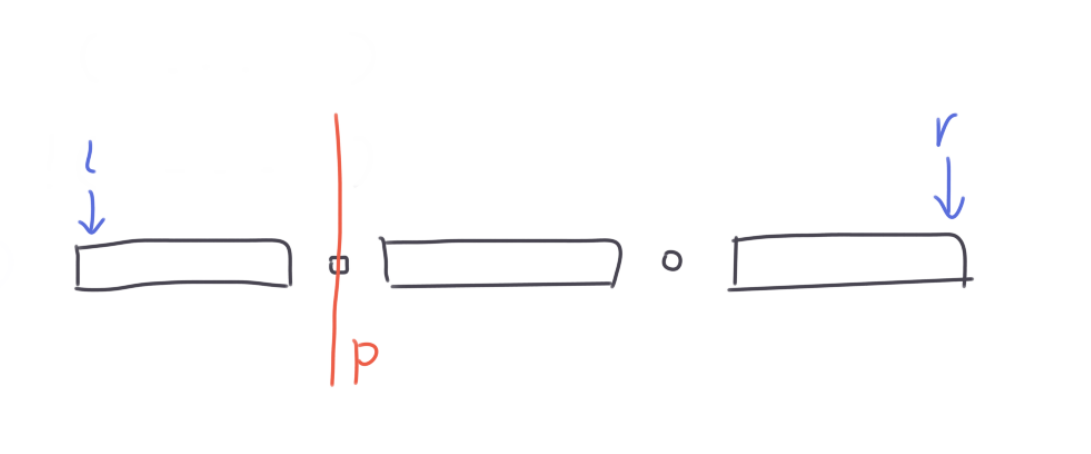
对于第三种情况,当前区间 [l, r] 不是一个表达式,而是由多个表达式中间用 &, |, <=, == 连接而成。我们找到第一个完整的表达式和第二个完整的表达式之间的符号作为表达式树上当前节点的符号,然后把区间一劈两半,递归建立左边和右边的表达式树,如下图
按照以上方法建树,样例二的第二组数据建成的表达式树就如下图:
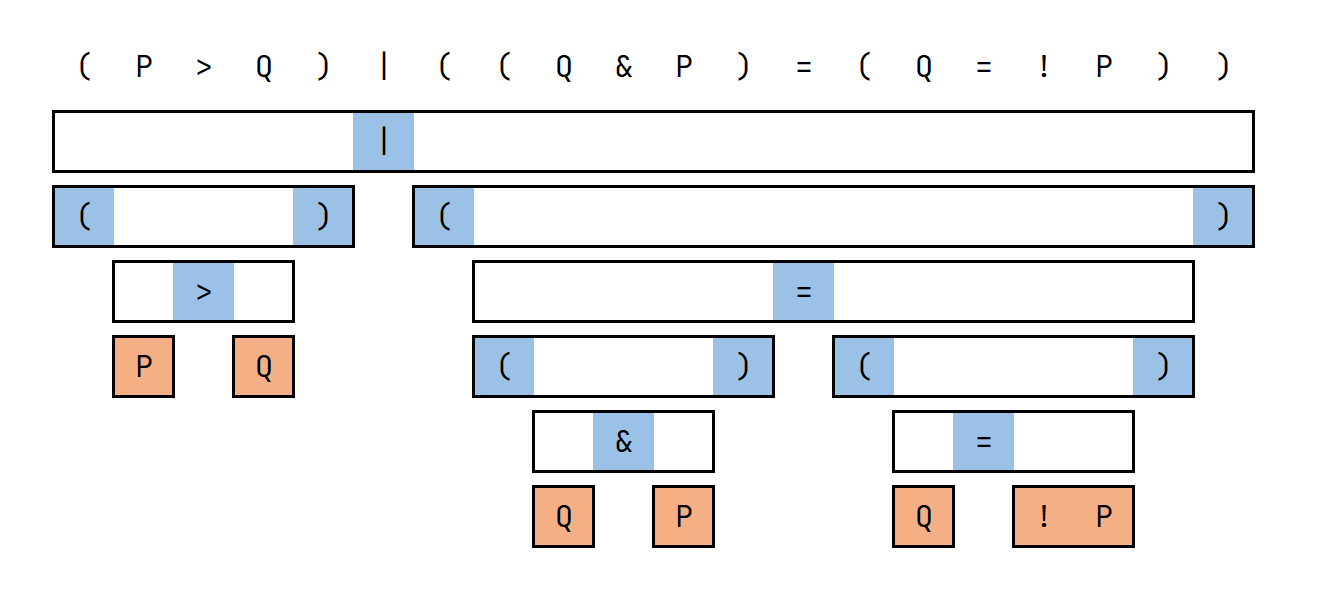
分析复杂度:无论哪一种情况,我们都必须在扫描完整个 [l, r] 区间之后才能确定,复杂度 \(O(n^2)\),良好实现可以获得 80pts 的好成绩
优化
如何加速这个过程?瓶颈在于:
1、我们怎么一眼看出某一段表达式是不是形如 !(...) 或者 (...) ?
2、对于第三种情况,我们怎么一步找到要劈开的位置?
优化方法如下:我们对括号匹配进行一遍分析。定义数组 match[],match[i] 表示,在 i 位置上的括号所匹配的另一半括号的位置。若 i 位置上不是括号,则 match[i] = -1。match[] 数组可以借助栈 \(O(n)\) 处理出来
这样,对于第一种和第二种情况,我们只需要看一看左边这个括号的 match[] 是不是右端点就行了
对于第三种情况呢?我们可能会想:从左往右扫,一旦碰着一个左括号,就跳到它的右括号去,然后再往后走一格就是我们要劈开的位置。如下图
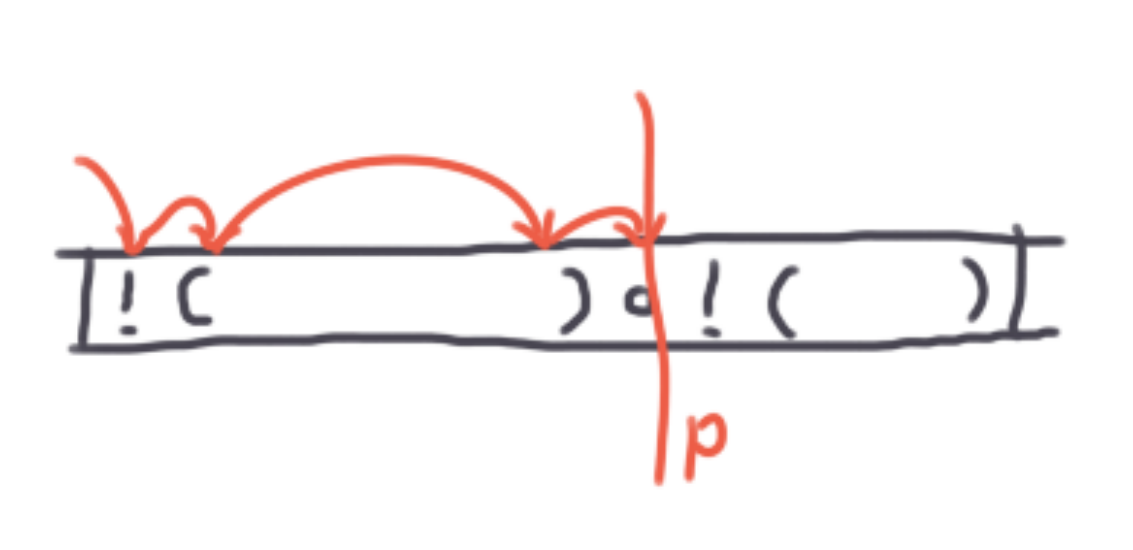
这看起来很对,也几乎就是对的了,但是依然能被卡掉。考虑下面这个样例:
!!!!!!!!!!!!!!!!!!!!!!!(...) & (...)
由于 ! 这个烦人的存在,我们从左往右扫的时候必须把第一个表达式之前的 ! 挨个点名。那么如果这一串 ! 很长很长的话,我们每次都要近似走 \(O(n)\) 格,复杂度就退化成了 \(O(n^2)\)
解决办法就是,再对所有的 ! 进行一波分析,如果某一段 ! 有奇数个,就留下一个;如果有偶数个,就全都扔掉。这样,每一段 ! 最多有一个,我们就怎么都卡不掉了。一次判断 \(O(1)\),建树复杂度是 \(O(n)\)
实现问题
这种题目普遍细节亿堆。贴一份一般实现的代码
这里为了减常,对于这样的:
(((((((...)))))))
或者夹杂着 ! 的:
!!!(!!(!!!!(!(...))))
我们都把它们层层剥去,只留下最里面的表达式。不再留一种无用的 () 运算符
这样树上会少很多节点,节约递归开销
// xiwon. //
#include <bits/stdc++.h>
using namespace std;
const int N = 200010;
int n; char s_[N];
string s;
int NODE_cnt, link[N], match[N], flag[N], appear[30], root;
int ls[N], rs[N], aloc[30];
char opt[N];
vector<char> vec;
void init() {
s = ""; NODE_cnt = root = 0; // 一堆清空 qwq
memset(link, 0, sizeof link);
memset(match, -1, sizeof match);
memset(flag, 0, sizeof flag);
memset(appear, 0, sizeof appear);
memset(ls, 0, sizeof ls), memset(rs, 0, sizeof rs);
memset(opt, 0, sizeof opt); vec.clear();
for (int i = 1; i <= n; i++) // 去掉多余的 '!'
if (s_[i] == '!') {
int flag = 0;
for ( ; s_[i] == '!'; i++) { flag ^= 1; } i--;
if (flag) s.push_back('!');
} else s.push_back(s_[i]);
n = s.length(); // 重置长度
static stack<int> sta;
for (int i = 0; i < n; i++) // 分析括号匹配
if (s[i] == '(') sta.push(i);
else if (s[i] == ')') {
match[i] = sta.top();
match[sta.top()] = i;
sta.pop();
}
}
inline pair<int, int> div_seg(int l) { // 切分出从 l 开始的一段表达式
// 分为四种情况:
// 1. (...) 2. !(...)
// 3. A 4. !A
if (s[l] == '!') {
if ('A' <= s[l + 1] && s[l + 1] <= 'Z') return make_pair(l, l + 1); // 4
else return make_pair(l, match[l + 1]); // 2
}
if ('A' <= s[l] && s[l] <= 'Z') return make_pair(l, l); // 3
return make_pair(l, match[l]); // 1
}
int build(int l, int r) {
int x = ++NODE_cnt; // 分配节点编号
while ((match[l] == r) || (s[l] == '!' && match[l + 1] == r)) { // 把外面套着的括号一层一层剥去
// 形如: (...) 或者 !(...)
if (s[l] == '!') l += 2, r--, flag[x] ^= 1; // 第二种情况
else l++, r--; // 第一种情况
}
if (r - l + 1 <= 2) { // 到达边界, 形如 !A 或者 A
if (r - l + 1 == 2) flag[x] ^= 1, link[x] = s[l + 1], appear[s[l + 1] - 'A'] = true;
else link[x] = s[l], appear[s[l] - 'A'] = true;
return x;
}
pair<int, int> seg = div_seg(l); // 切分出第一段完整的表达式的区间
ls[x] = build(seg.first, seg.second); // 左右递归
opt[x] = s[seg.second + 1]; // 当前节点的符号
rs[x] = build(seg.second + 2, r);
return x;
}
bool calc(int x) { // 计算以 x 为根的表达式树的值
if (link[x]) return flag[x] ? !aloc[link[x] - 'A'] : aloc[link[x] - 'A']; // 叶子
bool lans = calc(ls[x]), rans = calc(rs[x]), nowans = 0;
switch (opt[x]) {
case '&': nowans = lans && rans; break;
case '|': nowans = lans || rans; break;
case '>': nowans = lans <= rans; break;
case '=': nowans = lans == rans; break;
}
return flag[x] ? !nowans : nowans; // 如果具有取反属性就取反再返回
}
int main() {
while (~scanf("%s", s_ + 1)) {
n = strlen(s_ + 1);
init(); // 去掉多余 `!` 并且分析括号匹配
root = build(0, n - 1); // 建表达式树
for (register char k = 'A'; k <= 'Z'; k++) // 找出都有哪些字符出现了
if (appear[k - 'A']) vec.push_back(k);
for (register int s = 0; s < (1 << vec.size()); s++) { // 枚举取值情况
for (register unsigned int i = 0; i < vec.size(); i++)
aloc[vec[i] - 'A'] = (s >> (vec.size() - 1 - i)) & 1;
printf("%d", (int)calc(root)); // 计算并输出
}
puts("");
}
}
/*
!!!(!!(!((!!(A&B)))))
!!!(!!(!((!!(!A&B)))))
!!!(!!(!((!!!(!A&B)))))
(P>Q)|((Q&P)=(Q=!P))
*/
为了方便理解,我再写上变量的意义吧 qwq (真·良心题解
s_[]表示初始读入的字符串s在分析完!之后的字符串n字符串长度NODE_cnt节点的编号分配器link[]如果节点x是一个叶子,那么link[x]存储对应的字符(比如P,Q这些),否则link[x] = 0match[]已说flag[]如果flag[x] = 1说明计算完节点x子树的值之后要取反再返回appear[]辅助数组,如果appear['B' - 'A'] = 1说明字符B在字符串中出现了root表达式树的根节点编号ls[], rs[]一个节点的左右儿子编号aloc[]分配每个简单命题的具体值(0 / 1),用以在叶子的时候取出opt[]表达式树上每个节点上的运算符号vector<char> vec其中是所有出现过的简单命题,用以分配具体值
相信聪明的大家一定能研究明白上面这代码在写什么(吧 ?)
附.
后缀表达式当然可以,只不过会有亿点烧脑(?),可以自行研究一下。关键点还是在于 ! 运算的特殊性 —— 单目运算符,又是前置。
更多上流科技详见神 \(\mathtt{tiger2005}\) 的表达式求值三连 Part1,Part2,Part3。深修可以习得表达式真法(雾
以及,如果您缺少了大模拟刷可以尝试此题以获得良好体验:UOJ #98


 浙公网安备 33010602011771号
浙公网安备 33010602011771号