高光谱气体浓度反演方法学习笔记
主要是是Total 和 Onera 这两个组织研发的 IMGSPEC算法,借助加拿大 Telops 公司的 Hyper-cam 仪器来完成。
来源于文章:Methane leak near real time quantification with a hyperspectral infrared camera [1]
作者:S. Doz, P.Y. Foucher, X. Watremez,法国
一、主要原理概介
估计重建气体不存在时的背景辐射。

化简得到:
将 \(L_B\) 用 \(L_{off}\) 表示,假设目标气体温度与气温一致(\(T_{gas}=T_{atm}\),气体温度扩散很快),可以进一步化简上式:
也就是说,目标气体的透射率 \(\tau_{gas}\) 与 \(L_{on}\)、\(L_{off}\)、\(T_{atm}\) 有关。其中,\(L_{on}\) 就是传感器入瞳处接受到的辐亮度,\(T_{atm}\) 就是大气温度,可以通过测量获取。问题的重点在于 \(L_{off}\) 的测量或者估算。按照如下思路在估计背景温度的时候需要大气透射率 \(\tau_{atm}\).
估计 \(\mathbf{L_{off}}\) 的的思路:
见国外一篇硕士论文:Performance evaluation of chemical plume detection and quantification algorithms[2]首先我们可以将背景当作黑体, 那么获取到背景黑体的温度就可以计算出其分谱辐射
目标气体(例如\(SF_{6}\))在波长范围内有吸收系数为 0 的部分,在对应波长处,有\(L_{on}(\lambda)=\tau_{atm}\cdot B(\lambda, T_{B})+(1-\tau_{atm})\cdot B(\lambda, T_{atm})\),气温 \(T_{atm}\) 和大气透射率 \(\tau_{atm}\) 已知,那么可以估计出来背景黑体的温度。进一步地,对于某种气体而言,透射率为 1 的部分不仅限于某一个波长位置点,那么对于所有透射率几乎为 1 的部分而言,可以用最小二乘估计等方法来拟合背景温度,这样得到的背景黑体温度应该更准确。
二、 基于正交子空间的背景重建方法
主要目的: 模拟\(L_{off}\)
见另一篇论文:Background Radiance Estimation for Gas Plume Quantification for Airborne Hyperspectral Thermal Imaging[3]
主要是用波段选择方法来重构背景辐射, 选择的波段处目标气体的吸收系数几乎为0。
备注: 该论文中探测气体时使用了杂波匹配滤波器(CMF),说明如下:
其假设某像素值 \(\mathbf{\overrightarrow{x}} \sim N(\mathbf{\overrightarrow{\eta_{k}}}, \sum_{v})\) ,即像素值服从独立多维高斯分布,这里的维度数为波段数。
使用聚类-波段选择-PCA-法对 \(\mathbf{L_{off}}\) 进行估算的过程如下:
在气体探测结束后,将区域分为气体区域和非气体区域进行考虑:
- 在非气体区域: \(\mathbf{L_{off}}=\mathbf{L_{on}}\),首先进行主成分分析,\(\mathbf{P}\) 来源于主成分分析:
\[\mathbf{L_{off}}=\mathbf{U_{off}}\cdot\mathbf{P^T}+\mathbf{E_{off}} \]其中,\(\mathbf{L_{off}}\) 大小是 \(N_{non}\times N_{B}\),\(N_{non}\) 表示非气体区域的像素数目, \(\mathbf{U_{off}}\) 的大小是 \(N_{non}\times N_{p}\), \(N_p\) 通常取 10 就足够了,\(N_p\) 表示背景辐射曲线主成分数量。\(\mathbf{P}\) 的大小是 \(N_{B}\times N_{p}\),\(\mathbf{E_{off}}\) 是残差矩阵。
- 在气体区域: \(\mathbf{L_{off}^{sb}} = \mathbf{L_{on}^{sb}}\),首先进行主成分分析,\(\mathbf{P^{sb}}\) 来源于主成分分析:
其中 sb 表示被选择的波段,在这些波段位置处,目标气体(已知气体)的透射率为 1 。\[\mathbf{L_{off}^{sb}} = \mathbf{L_{on}^{sb}}=\mathbf{U_{on}}\cdot\mathbf{{P^{sb}}^T}+\mathbf{E_{on}} \]其中,\(\mathbf{L_{on}^{sb}}\) 的大小是 \(N_{gas}\times N_{SB}\), \(N_{gas}\)表示气体区域的像素数目,\(\mathbf{U_{on}}\) 的大小是 \(N_{gas}\times N_{p}\) , \(\mathbf{P_{sb}}\) 的大小是 \(N_{SB}\times N_{p}\) , \(\mathbf{E_{on}}\) 表示残差矩阵。
目前只有 sb 波段处的 \(\mathbf{L_{off}}\) 被观测到,要想获取所有波段的 \(\mathbf{L_{off}}\),需要计算出 \(\mathbf{U_{on}}\) :\[\mathbf{U_{on}}=\mathbf{L_{on}^{sb}}\cdot\mathbf{{{P^sb}^*}^T} \]其中,\(\mathbf{{P^{sb}}^*}\) 表示 \(\mathbf{P^{sb}}\) 的伪逆矩阵(严格来说只有方阵才有逆)。
\[\mathbf{{P^{sb}}^*}=(\mathbf{P^{sb}}^T\mathbf{{P^{sb}}})^{-1}\mathbf{P^{sb}}^T \]然后,对于气体区域全波段而言:
\[\mathbf{L_{on}}=\mathbf{L_{on}^{sb}}\cdot\mathbf{{{P^sb}^*}^T}\cdot\mathbf{P^{T}} \]
本文对上述的波段选择方法进行改进之处在于:先进行图像K均值聚类。所以本文的方法称为 Clustering-Based Selected-Band Method(CSB Method)。
热红外高光谱可以获得气体的柱浓度信息,有广阔的应用场景[4]。
路过图床提供在线图片支撑
参考文献:


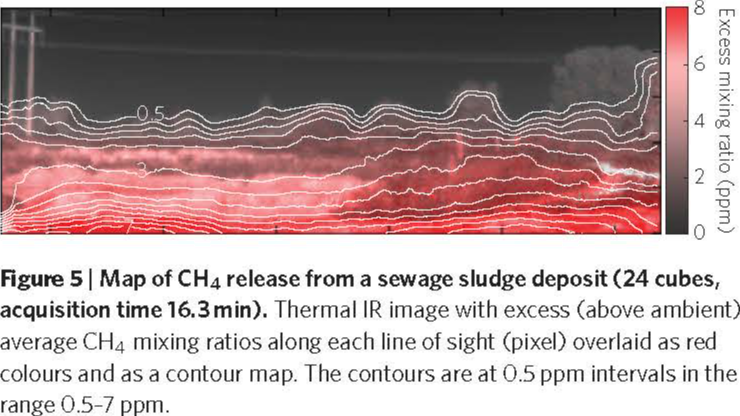 一种比较经典的高光谱气体浓度反演算法,侧重于背景重建。
一种比较经典的高光谱气体浓度反演算法,侧重于背景重建。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号