测试

数据结构 学习数据的存储与组织方法

数组、链表、栈、队列、树、图
用程序代码把现实情况的问题信息化
三方面：逻辑结构、物理结构、数据的运算

补一下C语言

关键字不能作为标识符
数据类型

1. 基本类型
2. 构造类型
3. 指针
4. 空类型
   基本数据类型
5. xxxxxxxxxx CREATE VIEW tot_credits(year,num_credits) AS SELECT year,sum(credits)FROM takesJOIN course ON takes.course_id = course.course_idWHERE takes.grade IS NOT NULL AND takes.grade = 'F'GROUP BY takes.course_idsql
6. 浮点型（实型）
7. 字符型
   输入和输出在库#include <stdio.h>

算法的时间、空间复杂度

字面意思orz

线性表linearList

具有相同数据类型的数据元素组成的有限序列，表示形式为
\(L = (a_1,a_2,\cdots,a_i,a_{i+1},\cdots,a_n)\)
注意，位序\(i\)从1开始，数组下标从0开始
操作：

• empty()：空true，否则返回false
• size()：返回线性表的大小（表元素的个数）
• get(index)：返回线性表中索引为index的元素
• indexOf(x)：返回线性表中第一次出现x的索引；如果不存在，返回-1
• erase(index)：删除索引为index的元素，索引大于index的元素其索引全部减1
• insert(index,x)：把x插入线性表中索引为index的位置上，再将index及其之后的元素索引全部加1
• output()：从左往右输出表元素

顺序表（数组）

用顺序存储的方式来实现线性表

• 优点：可随机存取，存储密度高
• 缺点：要求大片的连续空间，且改变容量不方便

顺序表的插入

1. 判断\(i\)的范围是否有效，存储空间是否已满
2. 将第\(i\)个元素及其以后的元素全部后移一位
3. 插入新元素\(j\)
4. 线性表长度加\(1\)
   时间复杂度\(O(n)\)

顺序表的删除

1. 判断\(i\)的范围是否有效
2. 将被删除的元素赋值给顺序表之外的空间\(e\)
3. 将第\(i\)个位置后的元素全部前移\(1\)位
4. 线性表长度减\(1\)
   时间复杂度\(O(n)\)

顺序表的查找

（1）按位查找
所有数据元素都是连续存放的，且大小全部相等。只需知道起始地址和数据大小，便可即时找到任意一个。
时间复杂度\(O(1)\)，这就是“随机存取”的特性
（2）按值查找，找到第一个元素值喂\(e\)的元素，并返回其位序
时间复杂度\(O(n)\)

链表

用链式存储的方式来实现线性表

• 优点：不要求大片的连续空间，改变容量也很方便
• 缺点：不可随机存取，要耗费一定空间存放指针

单链表的插入

（1）按位序插入
I 带头结点，在第\(i\)个位置插入指定元素\(e\)，先判断插入语句是否合法，不允许\(i = 0\)

1. 找到第\(i - 1\)个节点
2. 将第\(i - 1\)这个节点的指针连接上\(e\)所在的这个新节点
3. 将\(e\)所在的新节点的指针连接上第\(i\)个节点
   时间复杂度\(O(n)\)

II 不带头节点，则插入、删除第\(1\)个元素需要更改头节点指针\(L\)，写起来更麻烦

指定节点的插入

指定节点的后插操作都可以用循环找到并实现，那么怎么进行前插操作呢，见下图，连接新节点，让数据“跑路”



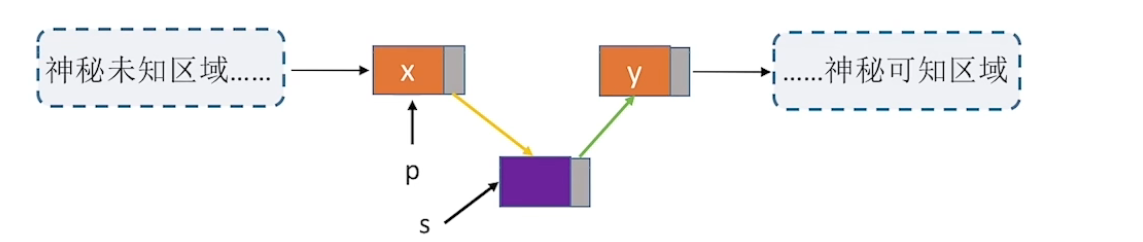
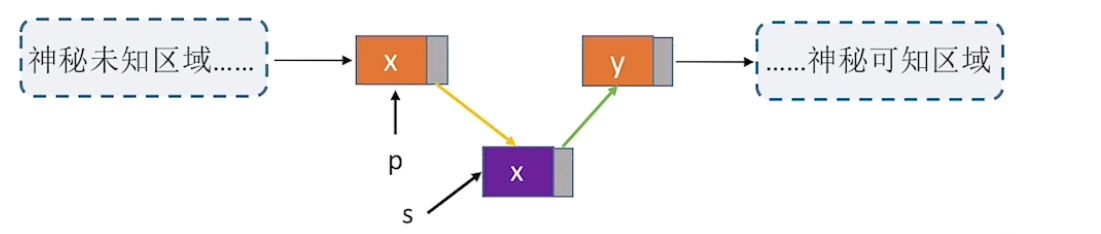
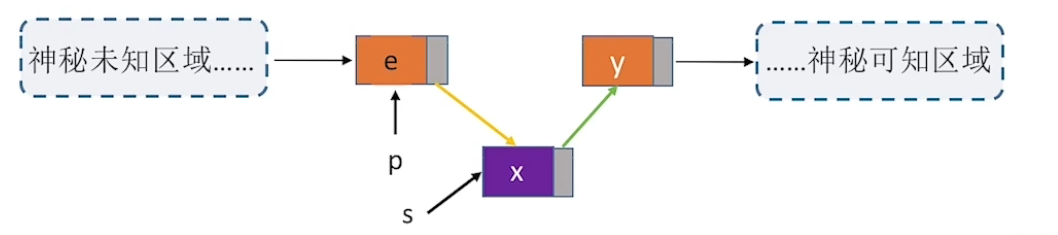
简直就是偷天换日啊，时间复杂度\(O(1)\)

单链表的删除

1. 找到第\(i-1\)个节点
2. 将这个节点的指针指向第\(i+1\)个节点
3. 释放第\(i\)个节点
   时间复杂度\(O(n)\)
   同样的，如果不带头节点要删除第\(1\)给元素，还要进行特殊操作，很麻烦，所以还是带上头节点把www

指定节点的删除

同样的问题发生了，删除指定节点\(p\)，还需要修改其前驱节点的next指针，对于前面未知且神秘的区域来说，该如何找到前驱节点呢
类比前插操作的实现，先将下一个节点\(q\)的元素复制进指定节点\(p\)


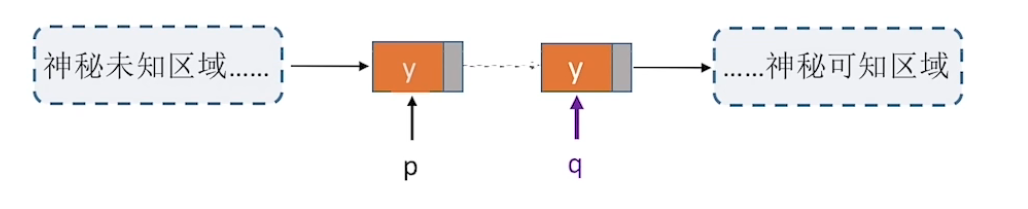
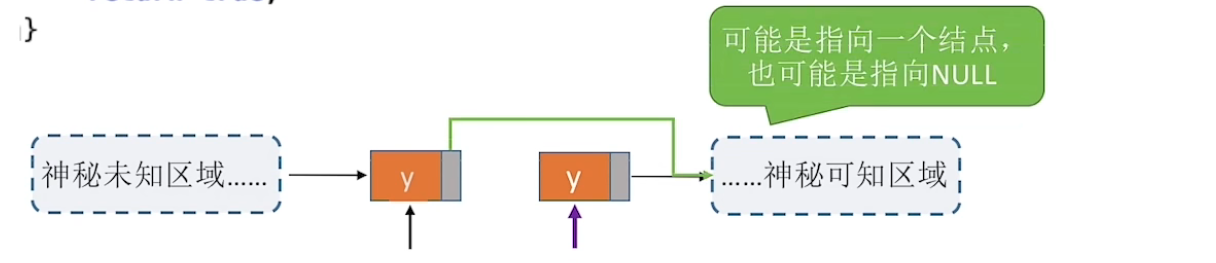
这样就实现了指定节点\(p\)的删除

单链表的查找

循环链表和头节点

在链表的前面加一个头节点，再将链表的尾节点与头节点相连，这样单项链表就成为了一个循环链表
经常对表头、表尾操作时，非常方便

双向链表

在后继指针的基础上，再添加前驱指针，就成为了一个双向链表

静态链表

静态链表分配一整片连续的内存空间，各个节点集中安置

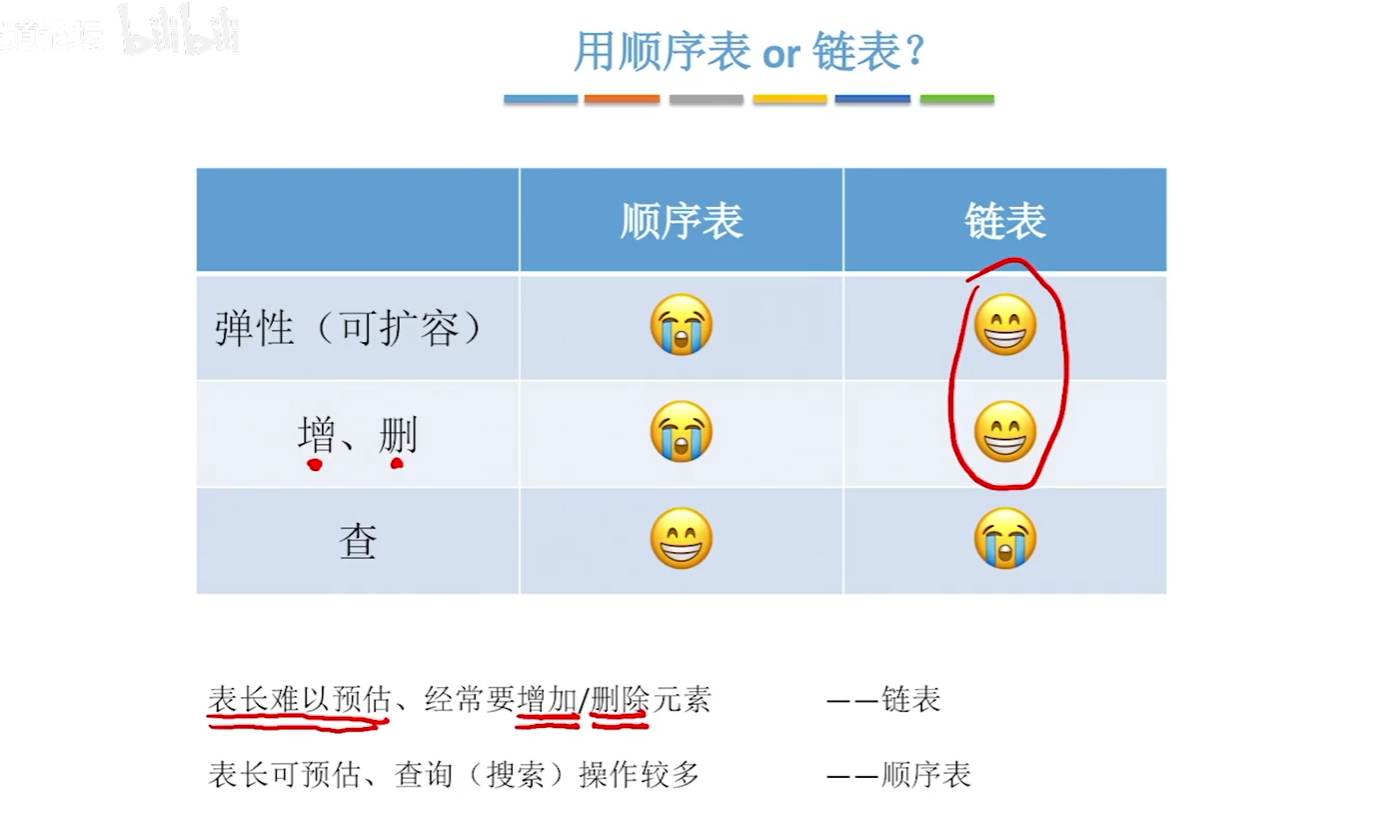
顺序表（数组）与链表的对比

• 逻辑结构：都属于线性表，都是线性结构
• 存储结构：
  顺序表：顺序存储，只需要知道起始地址，就可以立即找到第\(i\)个位置，支持随机存储，存储密度高；但大片连续空间分配不是很方便，且改变容量也比较麻烦
  链表：离散的小空间分配方便，改变容量方便；但不可以随机存储，且存储密度低
• 基本操作：创销、增删改查
  顺序表：预分配大片的连续空间；Length=0，静态回收、动态回收；插入/删除所有后继元素前移O（n）；按位查找O（1），按值查找无序O（n），如果元素有序O
  （log n），滴滴跳表
  链表：申明头指针（和头节点）；依次删除节点；插入/删除只需修改指针；查找永远O（n）
  
  

栈stack

逻辑结构、物理结构（存储结构）、数据的运算
栈是一种只允许一端进行插入或删除的线性表（整齐的一堆），后进先出（LIFO），叠碗盘子，烤串！

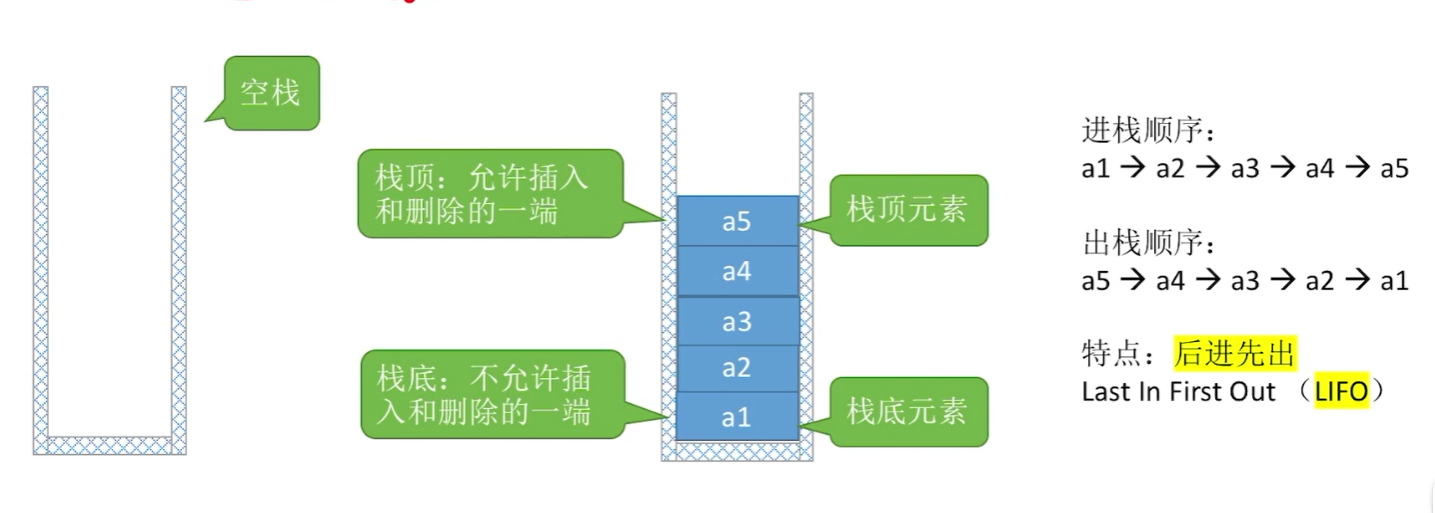
基本操作：

• empty()：空true，否则返回false
• size()：返回栈中的元素个数
• top()：返回栈顶元素
• pop()：删除栈顶元素
• push(x)：将元素x压入栈顶
  考题：进栈、出栈顺序，卡特兰（Catalan）数\(\frac{1}{n+1}C_{2n}^{n}\)
  记得分配一个栈顶指针！如下图top（），top== -1
  
  插入/删除时，top也要+1 / -1

队列queue

队列是一种只允许在一端进行插入，在另一端进行删除的线性表，先进先出（FIFO），排队，食堂打饭！

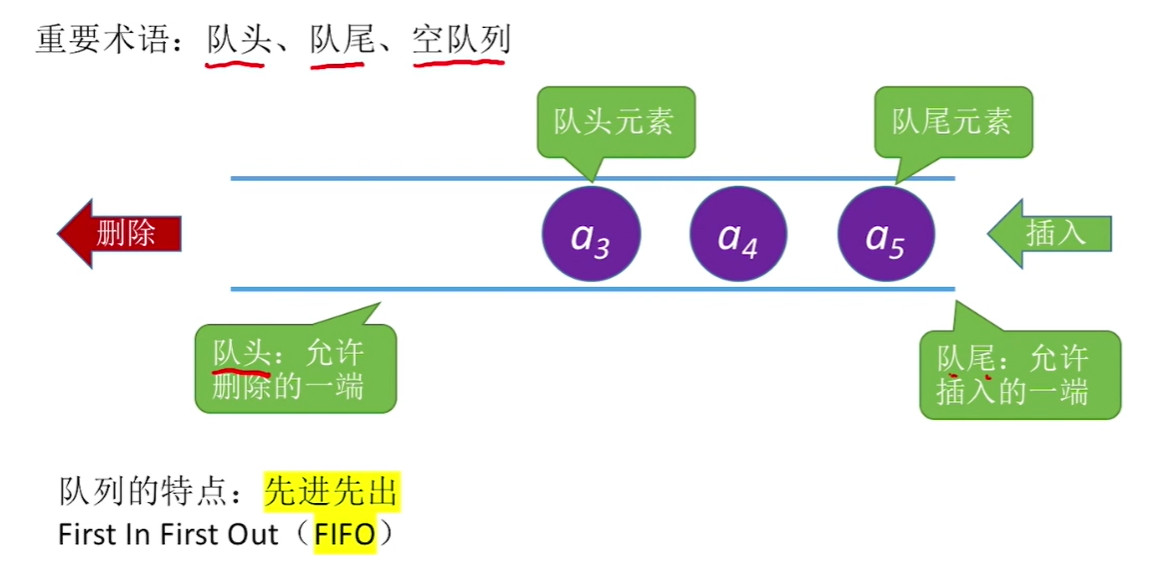
基本操作：

• empty()：空true，否则返回false
• size()：返回队列中的元素个数
• front()：返回队列头元素
• back()：返回队列尾元素
• pop()：删除队列首元素
• push(x)：把元素x加入队尾
  
  

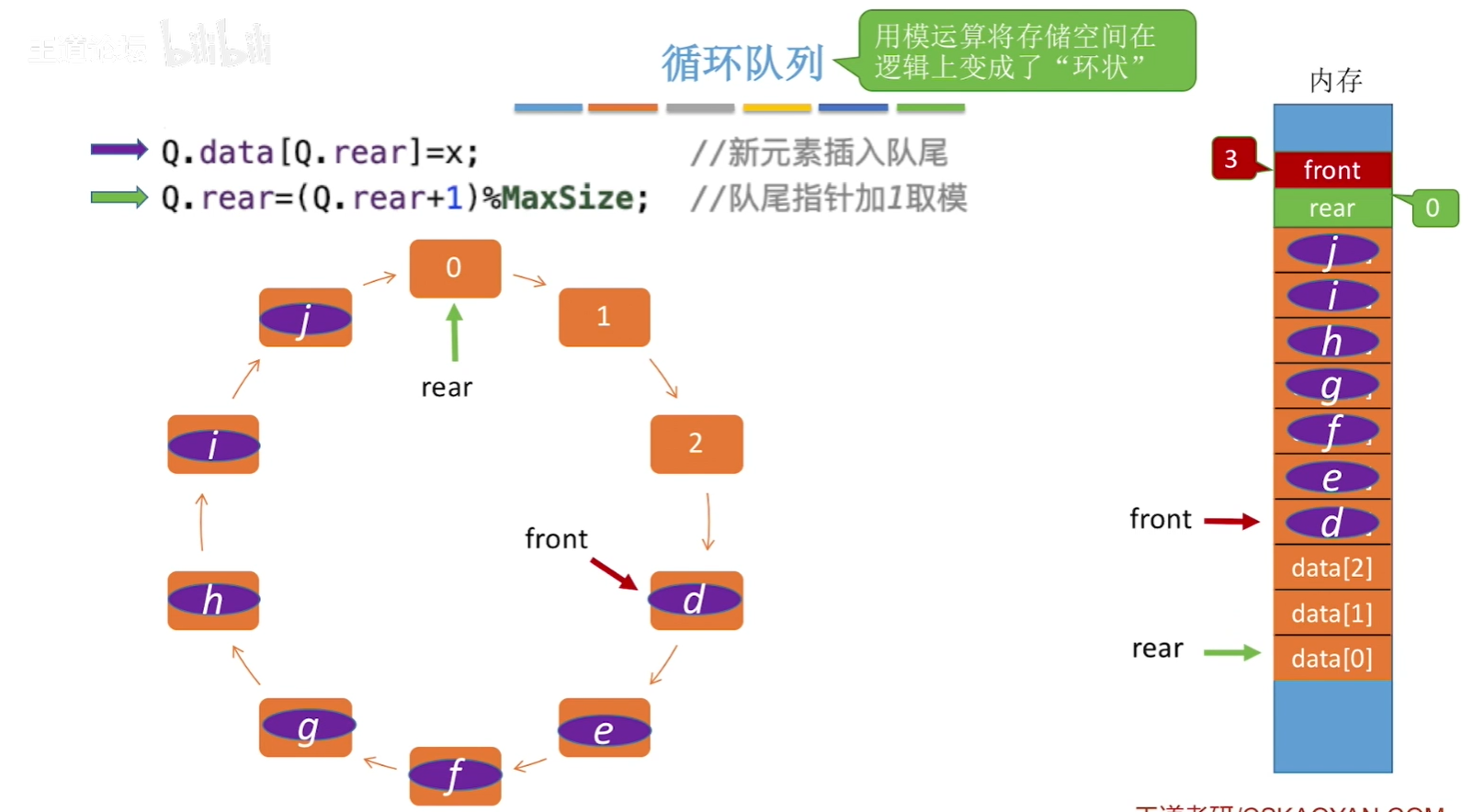
双端队列

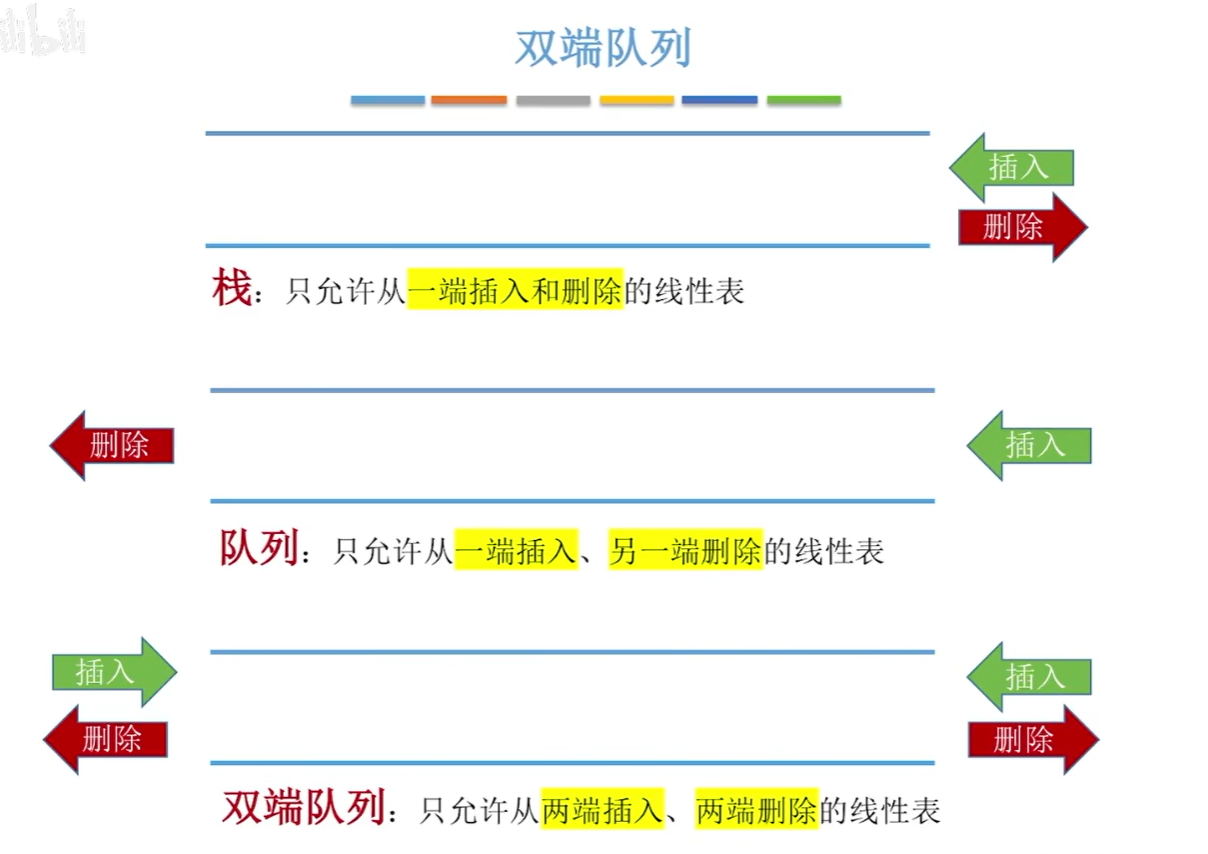
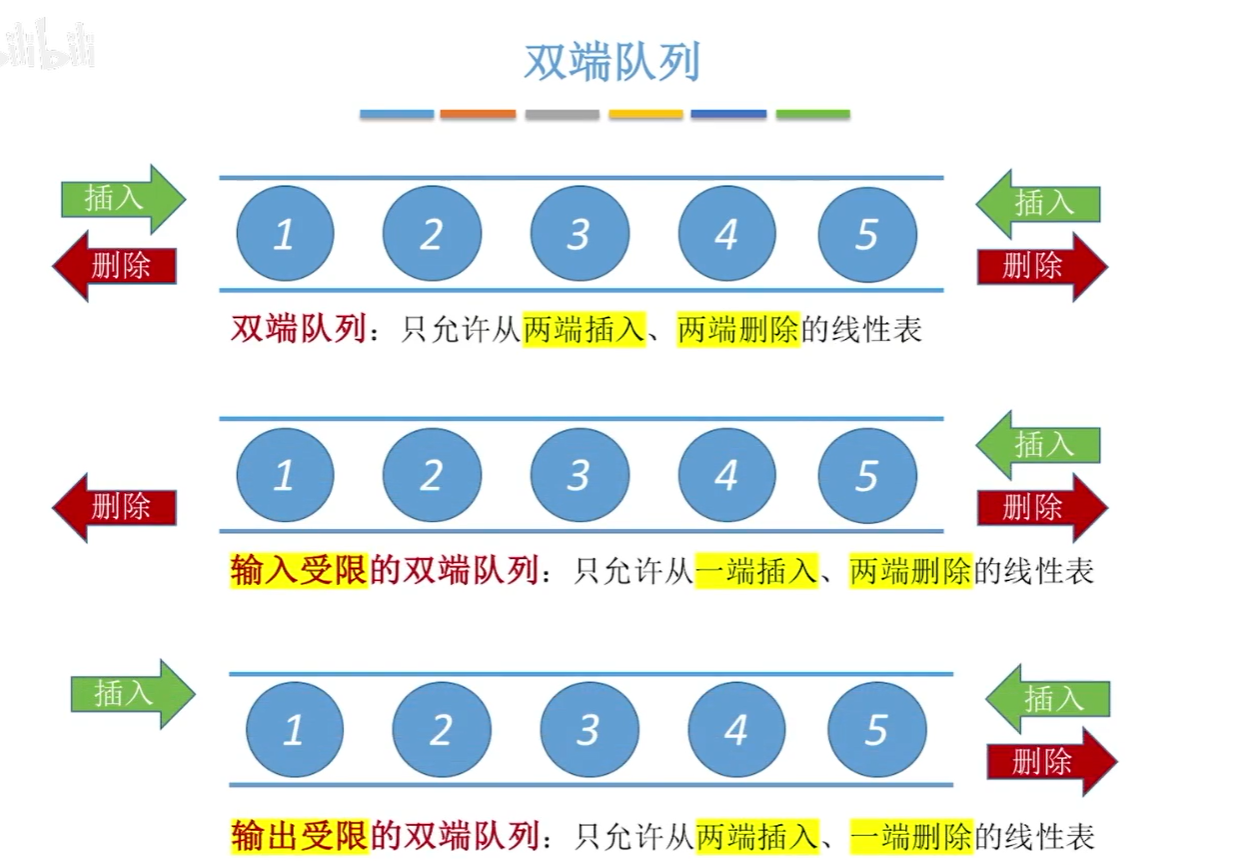
树tree

树的概念

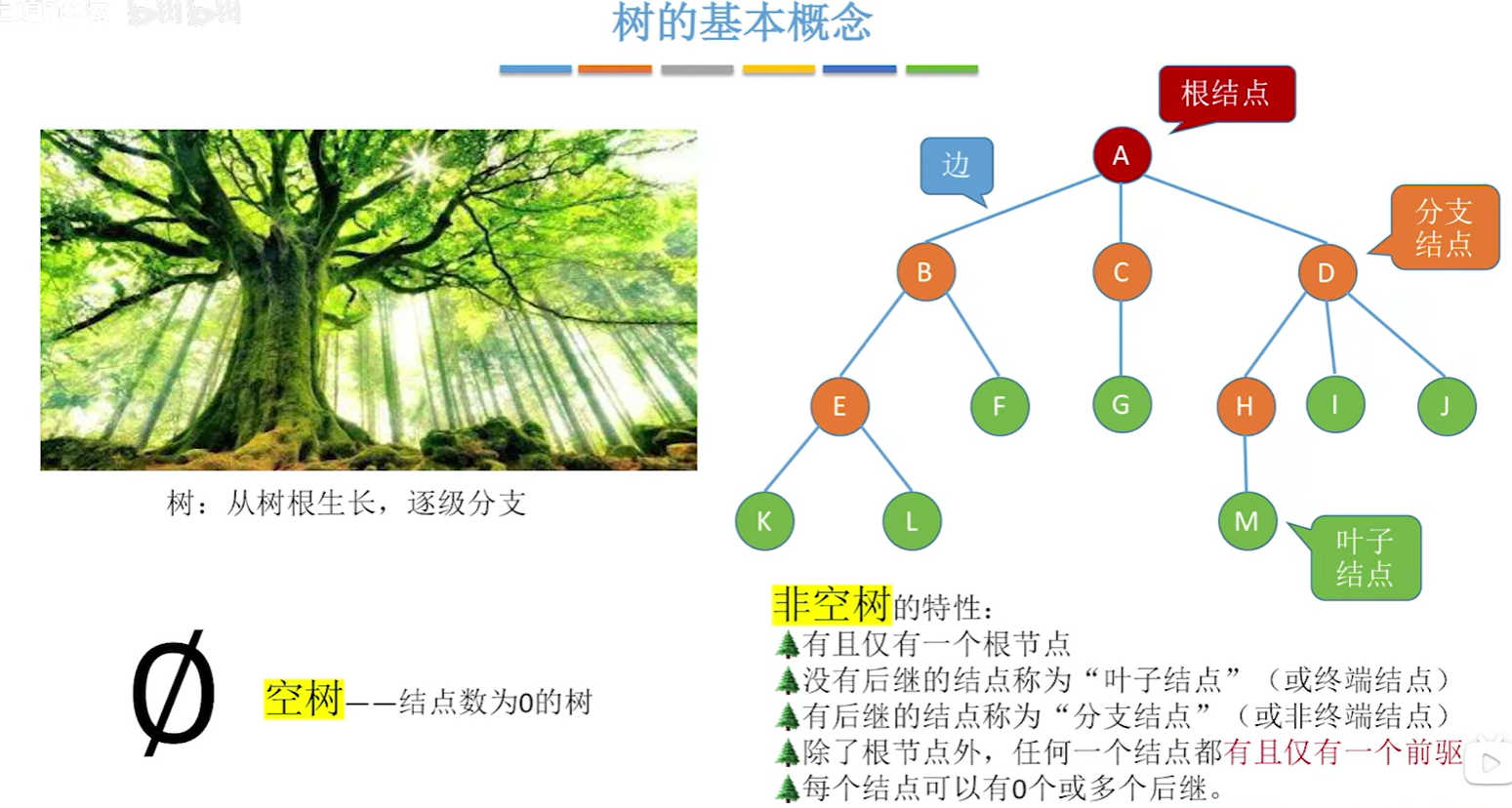
再次强调：除了根节点之外（它没有前驱），任何一个节点都有且仅有一个前驱！
补充一下子树的概念：

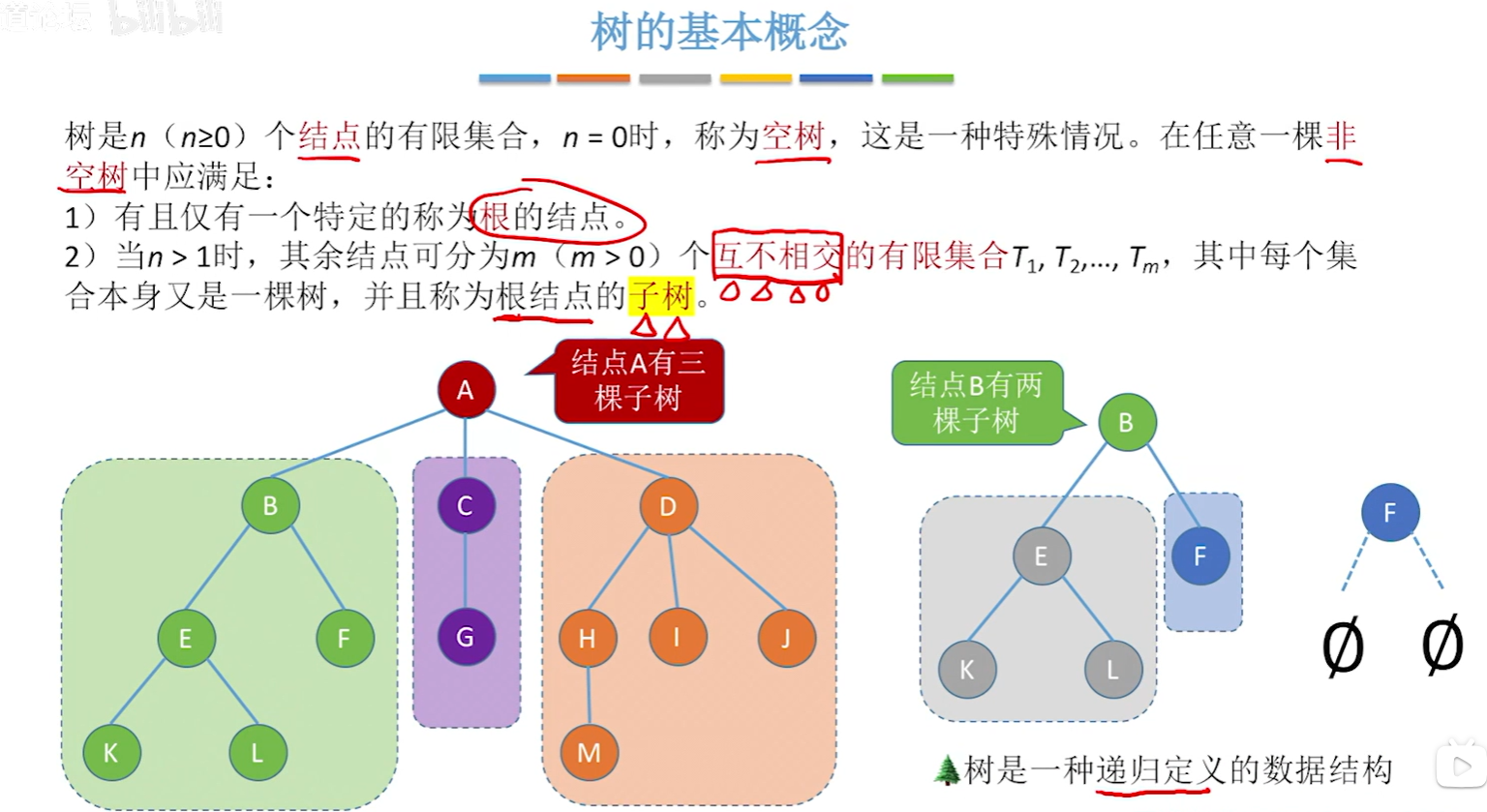
有点像文件夹，子标题，思维导图，俄罗斯套娃（

• 基本术语
  节点之间的关系描述术语来源于家谱，截了一张图
  

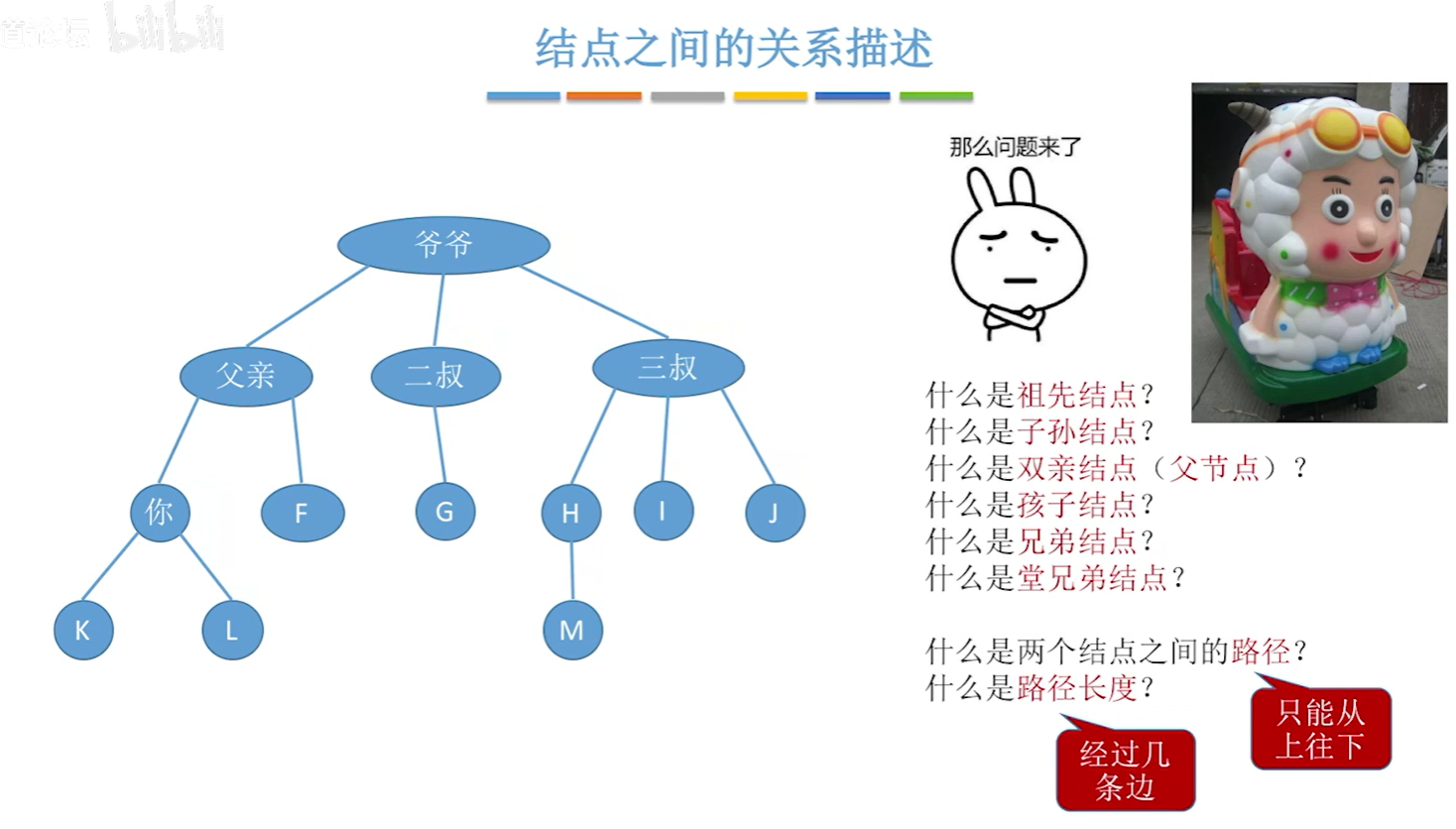
对于“你”来说，父亲、爷爷都是祖先节点；对于“爷爷”来说，下面全部节点都是子孙节点；对于“你”来说，直接前驱“父亲”就是双亲节点（父节点）；对于“父亲”节点来说，直接后继“你”和“F”就是孩子节点；“二叔”、“三叔”是“父亲”的兄弟节点；“G”"H"“I”“J”就是“你”的堂兄弟节点（这个不怎么用）
实在学不会可以听这首歌：

下面再来看几个非常非常重要的概念：

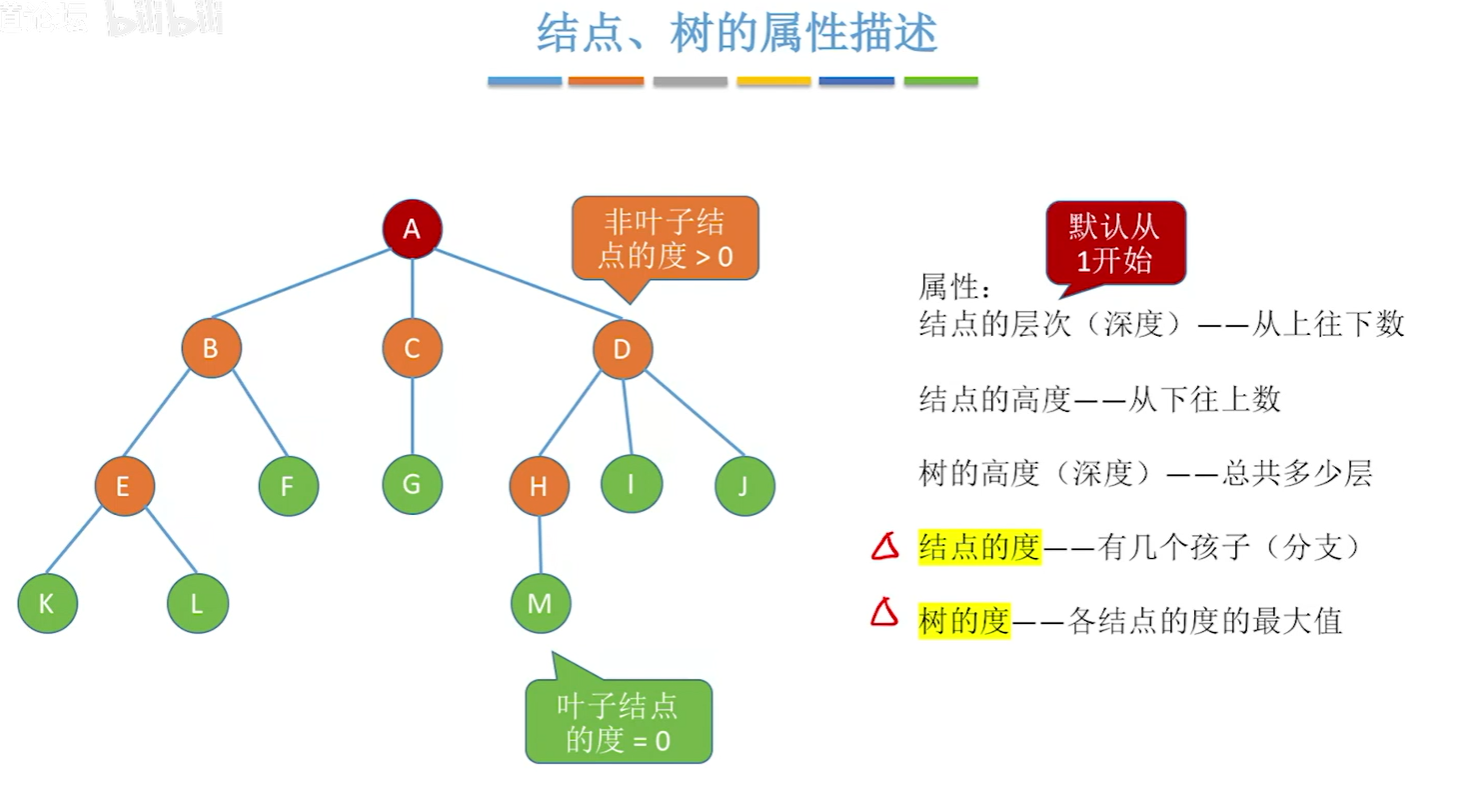
有序树和无序树的概念，只要弄明白此排名有无分先后即可：

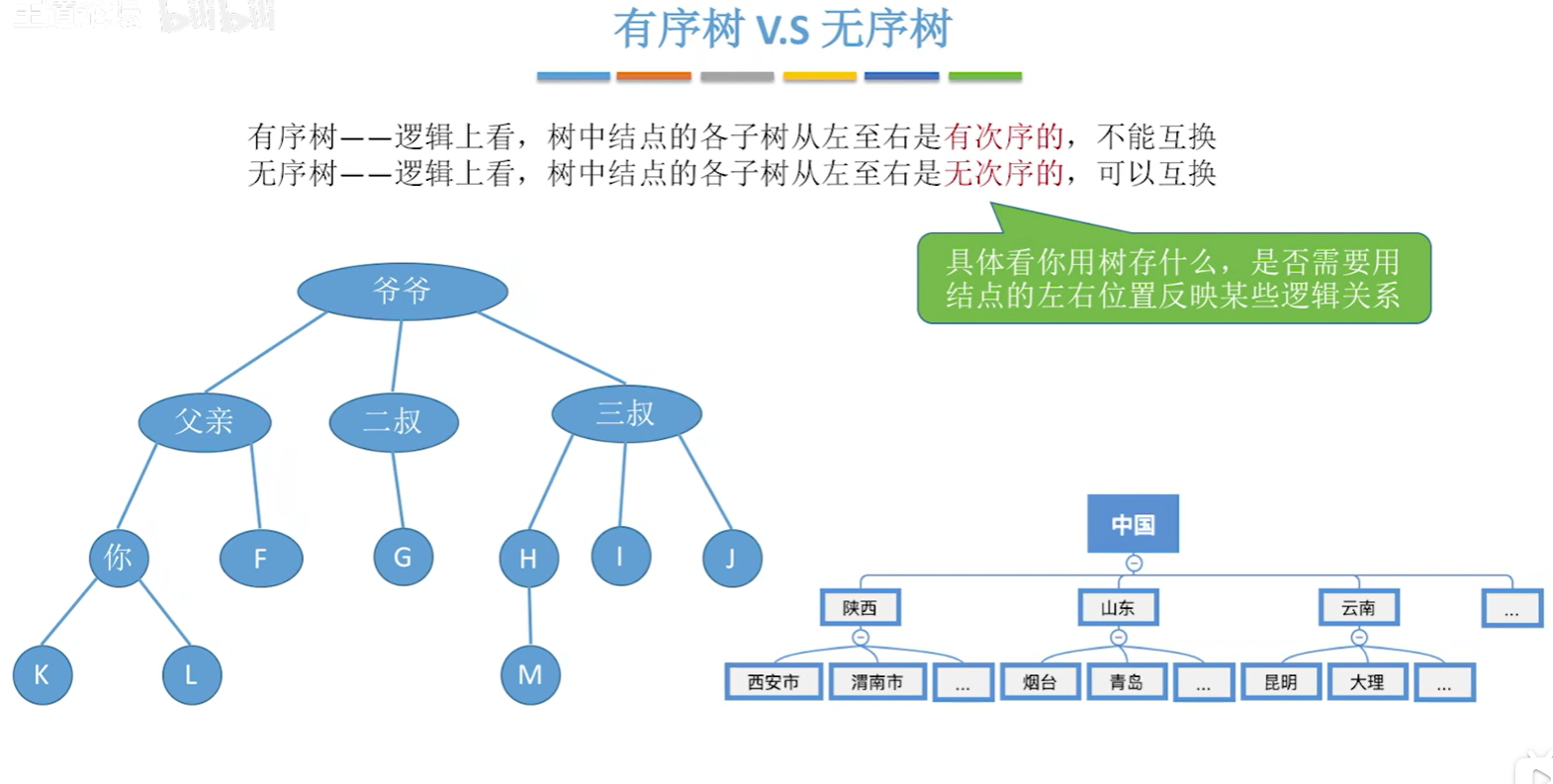
最后介绍一下森林，森林是由\(m(m \geq 0)\)棵互不相交的树组成的集合，如果把一棵树用作对一户人家的家谱的数据描述，那么就可以用森林来进行对全中国所有人家的家谱的数据描述
注意，允许有一棵树都没有的森林，也就是空森林的存在

树的性质

1. 节点数 = 总度数 + 1
   加一是因为根节点哦，其他的节点头上都有一根线相连

2. 度数为\(m\)的树 vs \(m\)叉树
   

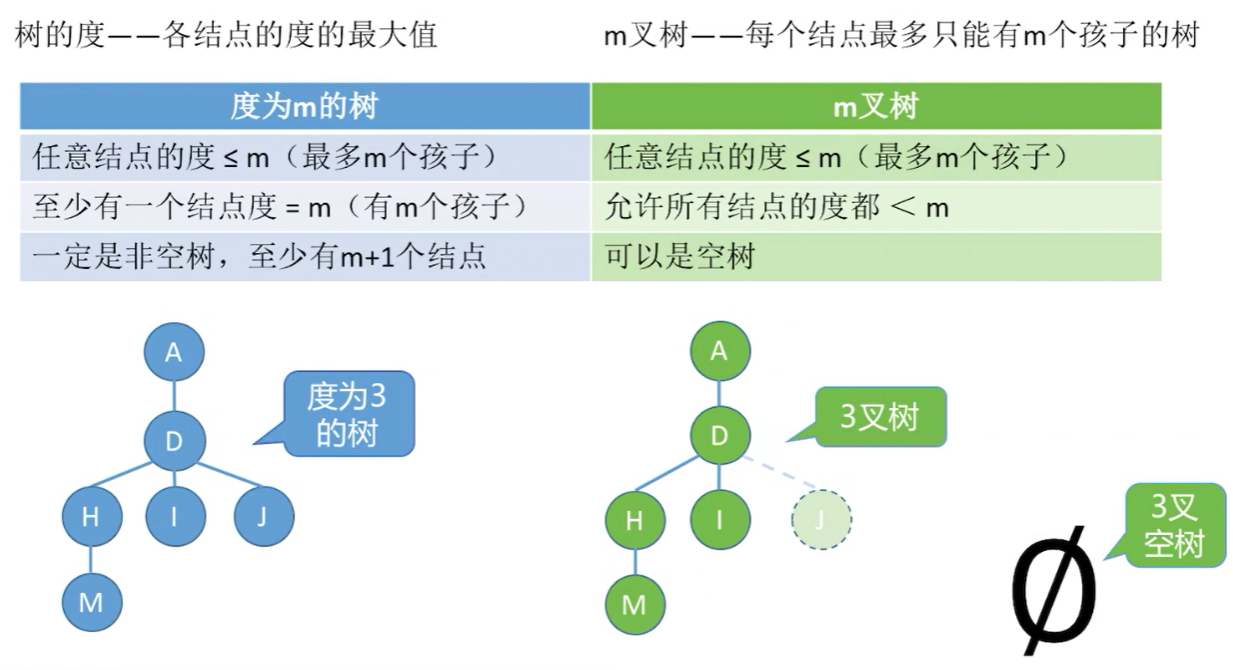
3. 度数为\(m\)的树第\(i\)层至多有\(m^{i-1}\)个节点\((i \geq 1)\)
   emmmm，比较明显的数学推理（？

4. 高度为\(h\)的\(m\)叉树至多有\(\frac{m^h - 1}{m - 1}\)个节点
   由性质3推导出来的，使用等比数列求和

5. 至于最少有多少个节点嘛
   如果是高度为\(h\)的\(m\)叉树，那就是一条完全线性结构，至少有\(h\)个节点；如果是高度为\(h\)、度为\(m\)的树，那就要满足至少有一层含有\(m\)个节点，其他的同理
   高度为4、度为3的树，最少节点数：\(4-1+3 = 6\)；高度为4的三叉树，最少节点数为：4
   

6. 具有\(n\)个节点的\(m\)叉树的最小高度应为：\([log_m (n(m-1)+1)]\)
   尽可能往宽里面长，结合之前的性质3，以及树的性质，推导过程：
   

二叉树

二叉树是一种由\(n(n \geq 0)\)个节点组成的有限集合，一般可以分为两类：

1. \(n = 0\)空二叉树
2. 由一个根节点和两个互不相交的左子树和右子树组成，其中左子树右子树它们又分别都是一颗二叉树
   这不还是一种递归定义嘛
   有两个特点：
3. 每个节点至多只有两棵子树
4. 二叉树是有序树，左右不可以颠倒！

二叉树的五种状态：

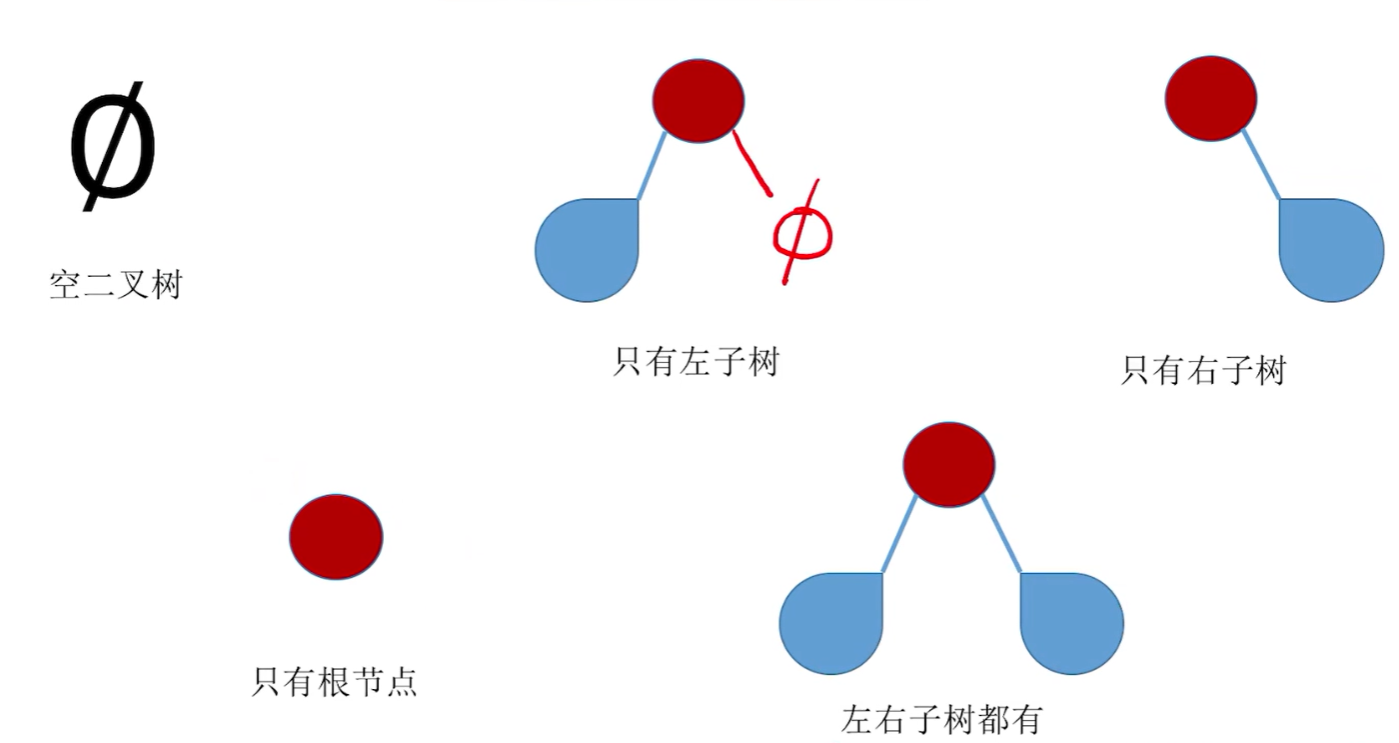
下面介绍几个特别的二叉树类型：

满二叉树 & 完全二叉树

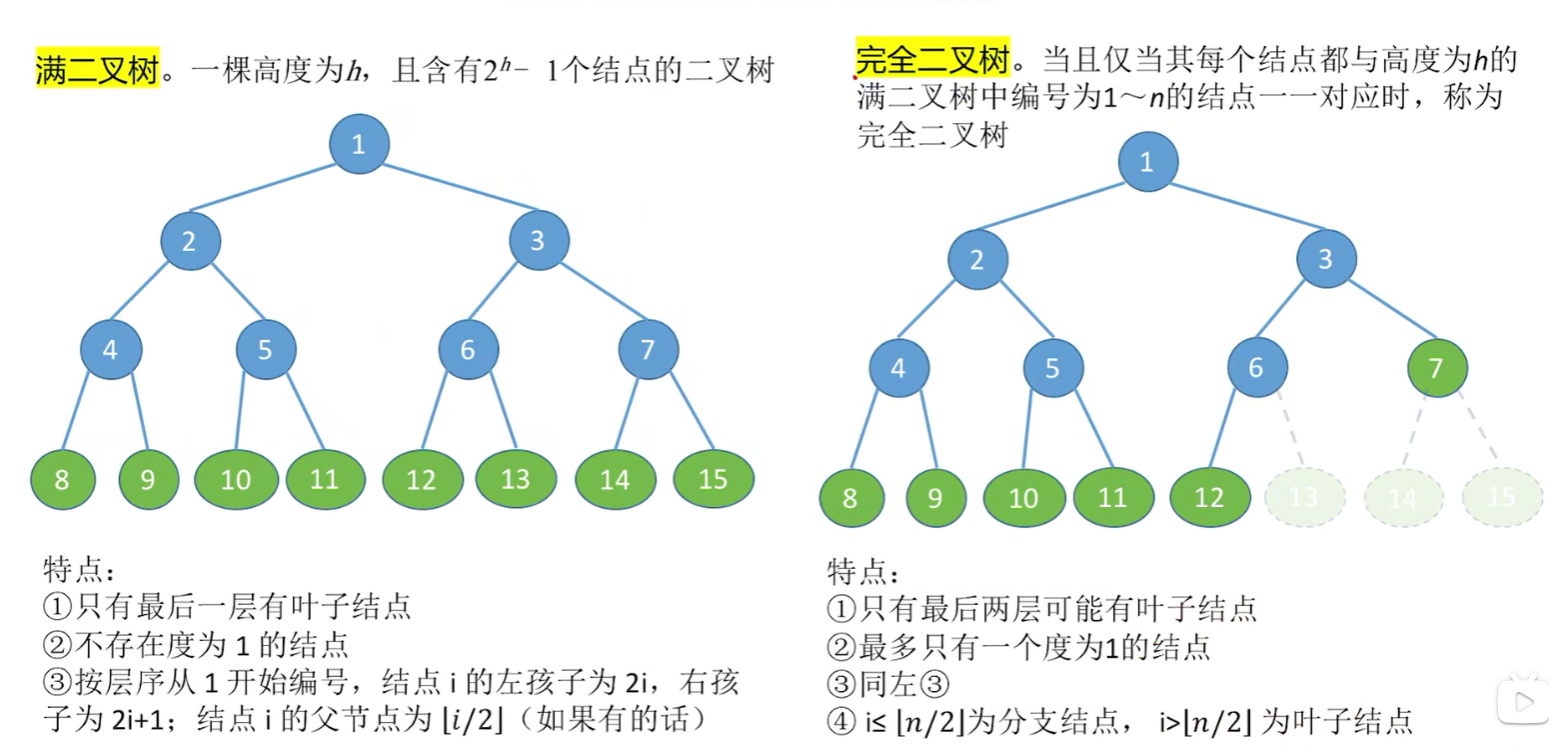
可以理解为，完全二叉树是满二叉树的一种子集，去掉了最大的若干个元素
对于完全二叉树来说，如果一个节点有孩子，那么这个孩子一定是左孩子，不然就不是完全二叉树

二叉树描述

数组描述

完全二叉树:按照二又树对元素的编号方法，将二叉树的元素存储在数组中。

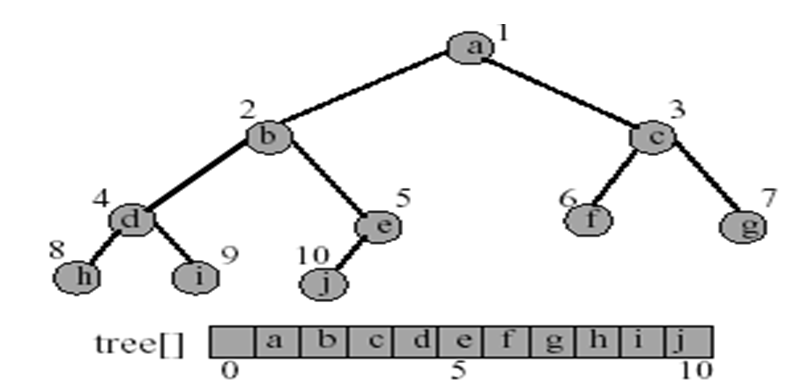
而二叉树就可以看作是部分元素缺失的完全二叉树，在对应索引位置上留空。

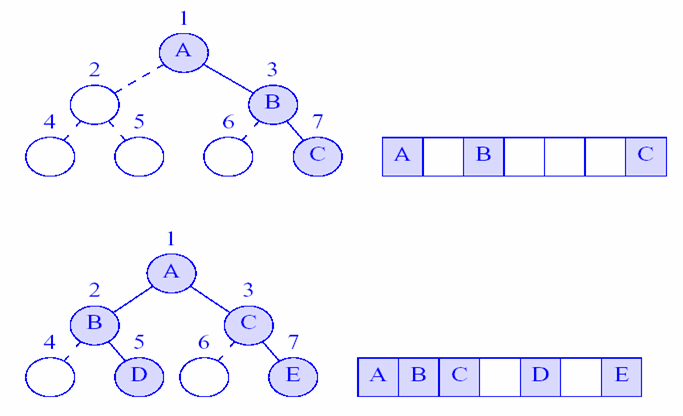
所以，一个有n个元素的二叉树需要的存储空间：\(n \to 2^n + 1\)，当出现右斜，二叉树存储空间达到最大。

链表描述

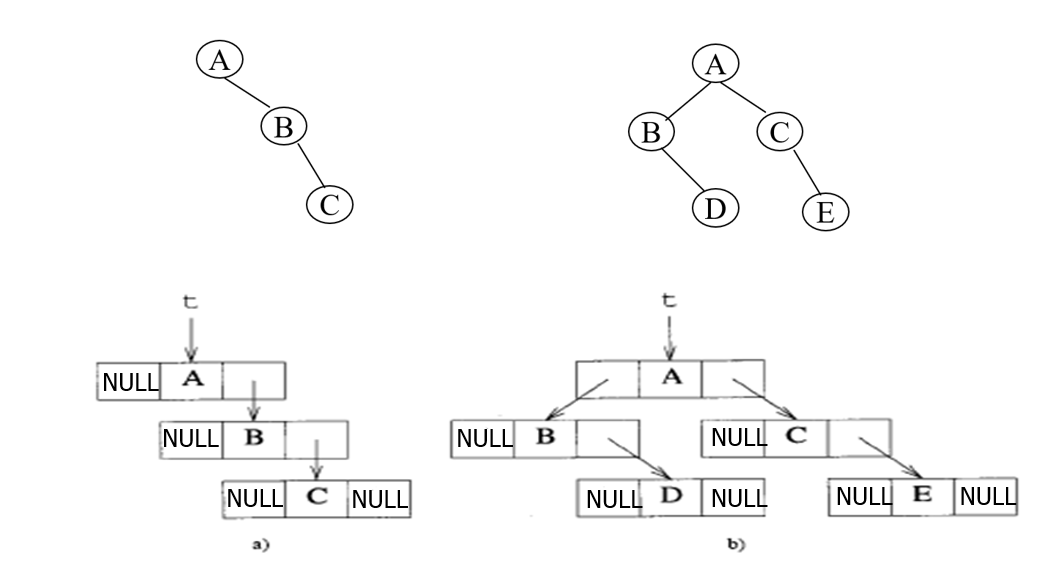
二叉树遍历方法

• 前序遍历：访问根元素；前序遍历左子树；前序遍历右子树
• 中序遍历：中序遍历左子树；访问根元素；中序遍历右子树
• 后序遍历：后序遍历左子树；后序遍历右子树；访问根元素

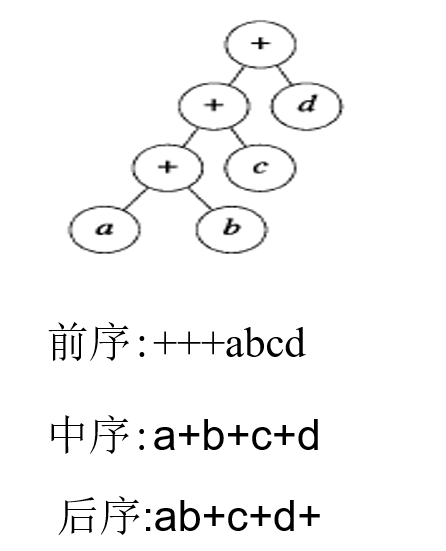
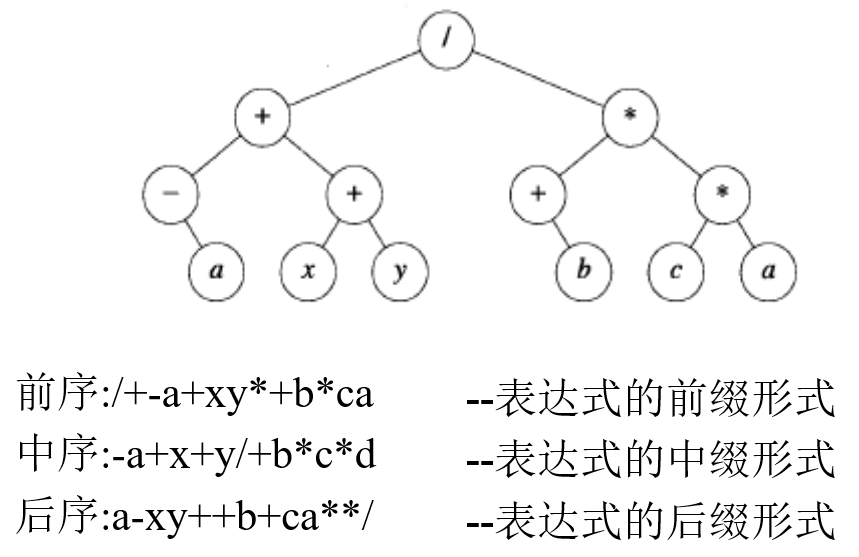
二叉排序树

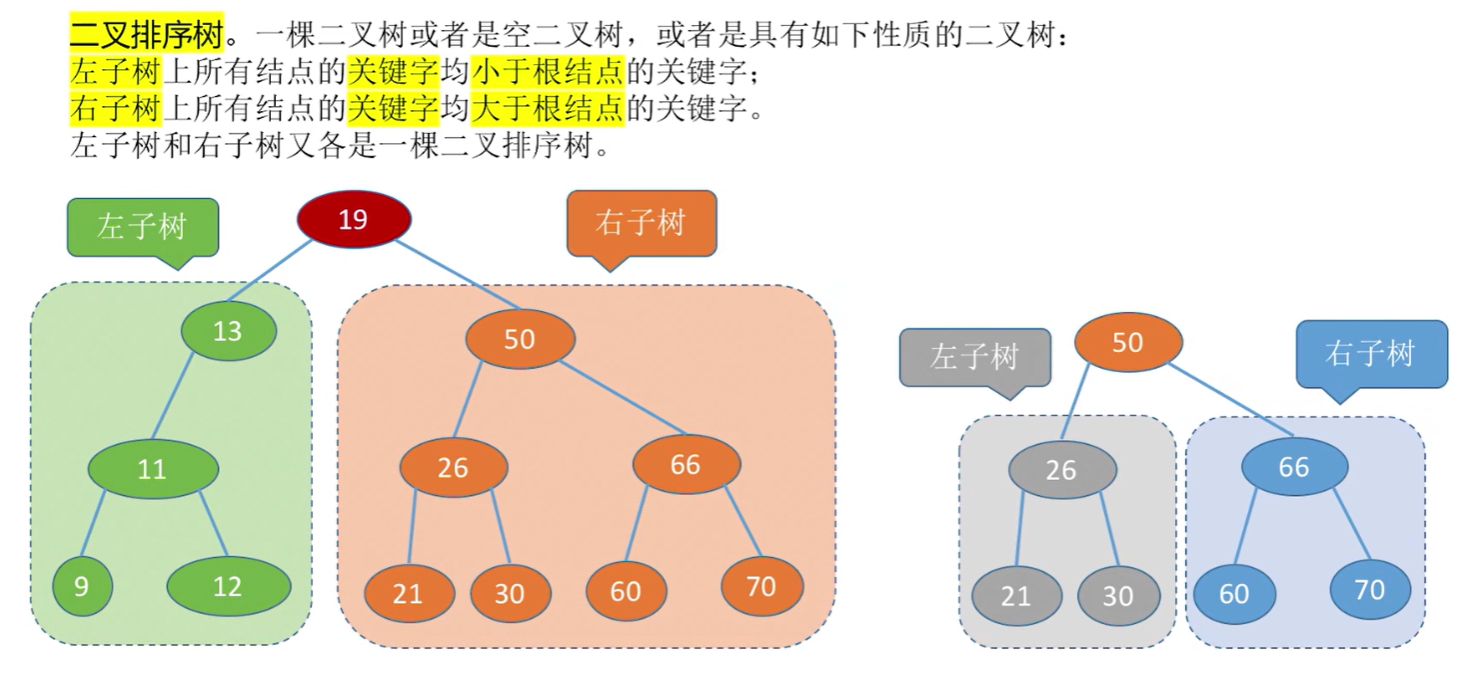
大小顺序：左中右，在这种结构下，能很迅速找到指定关键字
也是一个很有意思的递归定义

• 广度优先遍历 临时数据结构 ：队列
• 深度优先遍历 临时数据结构 ：栈

优先级队列

堆排序

搜索树

比调表和散列表有更好或类似的效果
尤其擅长顺序访问或按排名访问

• 二叉搜索树：可能为空的二叉树，可以不是完全二叉树

非空的二叉搜索树满足：

1. 每个元素都有唯一关键字
2. 根节点左子树的关键字一定小于根节点的关键字
3. 根节点右子树的关键字一定大于根节点的关键字（与堆？不同）
4. 根节点的左右子树都是二叉搜索树

• 索引二叉树：在每个节点添加一个“LeftSize”

操作
insert : O(height)
erase : 三种情况

1. p是树叶
2. p只有一个非空子树
3. p有两个非空子树

图

图（Graph）结构是一种非线性的数据结构
图在实际生活中有很多例子，比如交通运输网，地铁网络，社交网络，计算机中的状态执行（自动机）等等都可以抽象成图结构。图结构比树结构复杂的非线性结构。
图结构由两部分构成：

• 顶点：图中的数据元素
• 边：连接各个顶点的线
  下面主要介绍一下简单图，两种基本结构，分别为无向图与有向图

无向图

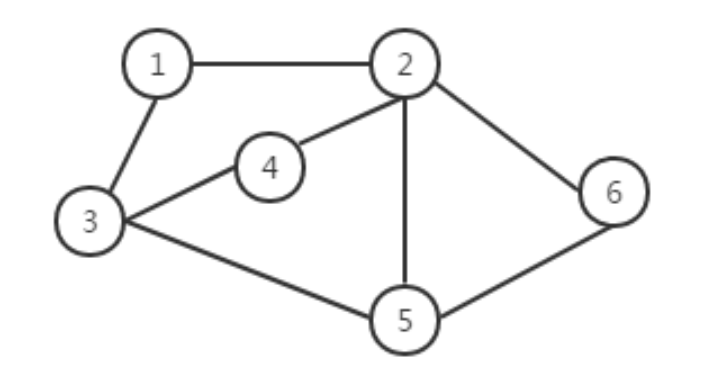
一般形式如上图所示，无向图最大的特点，便是边不具有方向性。顶点3(V3)与顶点5(V5)之间的边，既可以用(V3,V5)表示，也可以表示为(V5,V3)

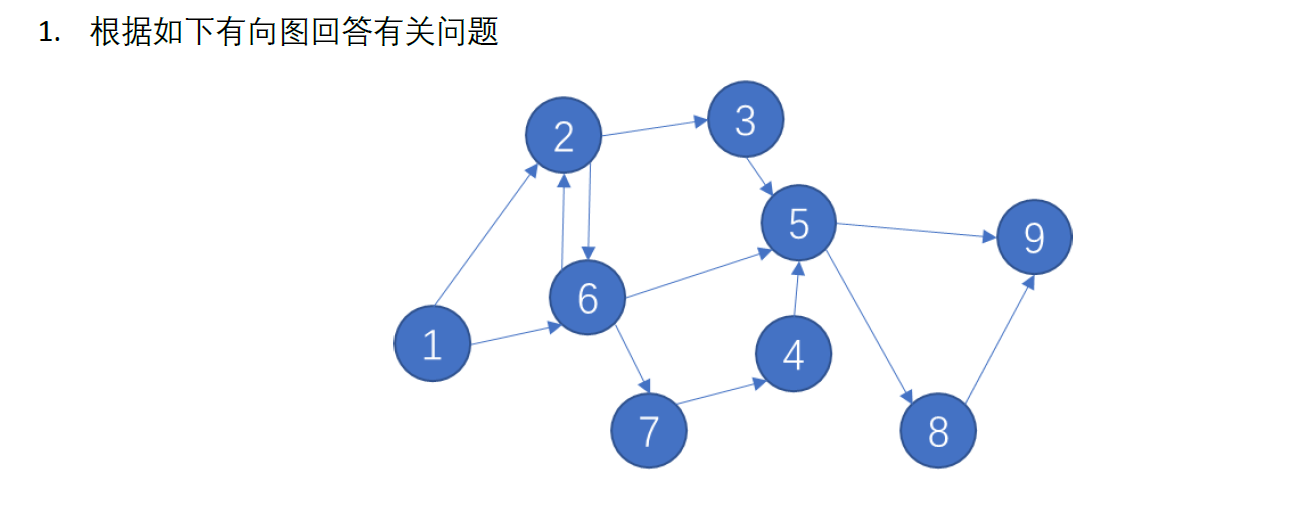
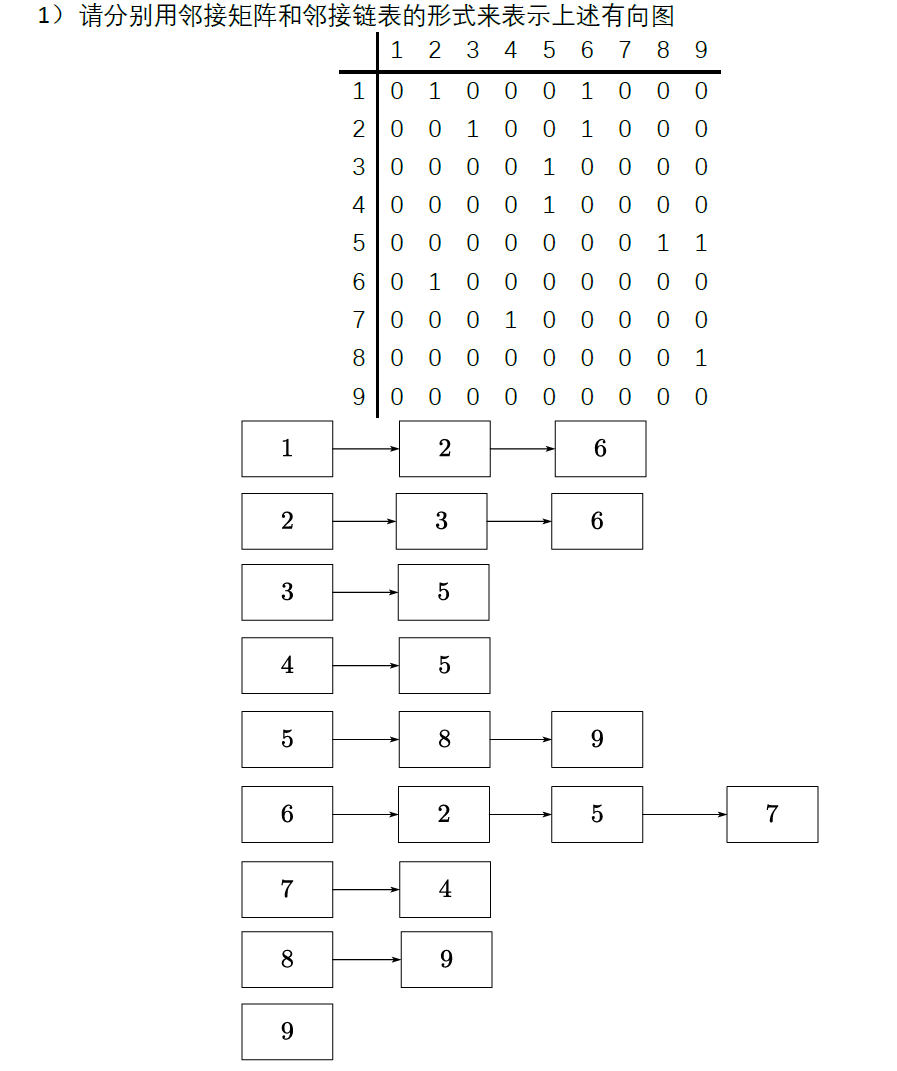
矩阵表示

权重 有无向 节点相连

链表表示

应用

路径问题

路径、简单路径