字符串 学习笔记
第一章 字符串处理
存储字符串
字符数组
可以使用 char s[] 的形式存储一个字符串。比如我们需令 \(s=\texttt{Hello}\),有两种定义方式:
-
char s[] = {'H', 'e', 'l', 'l', 'o', '\0'}。 -
char s[] = {"Hello"}。
注意无论是哪一种写法,字符串的最后一定都有一个特殊字符 \0,他代表着字符串的结束。所以如果你想存储一个长度为 \(n\) 的字符串,请把字符数组开到 \(n+1\),否则会产生数组越界。
这种 C 风格的字符串说白了就是和数组一样的,不过是存放的字符的数组。在头文件 cstring 里有一些函数可以辅助我们进行字符串的操作。
注意:不可以使用 char a[100]; a = b; 这样的形式来对一个字符串赋值。
在 C 中,有两个特殊的函数 sscanf 和 sprintf,他们相当于是以字符数组为输入、输出到字符串的 scanf 和 printf。用法如下:
sscanf(s, "%d", &n); // 从 s 中读取一个整数存储到 n
sprintf(s, "%d", n); // 把 n 输出到字符串 s 中
注意 \(s\) 的下标要从 \(0\) 开始。
char c;
c = getchar(); // 读取一个字符
scanf("%c", &c); // 与 getchar 一样 这两种方法都会读取到空格
cin >> c; // 这种方法不会读取到空格
char s[1000];
cin >> s; // 读取一个字符串
scanf("%s", s); // 与 cin 相同,注意没有取址符 &
gets(s); // 读取一行字符串,包括空格,但是不建议这么做,因为在 C++14 中会 CE.
int i = 0; while ((s[i] = getchar()) != '\n') ++i;// 这么做也可以读取一行字符串,推荐使用这个
String 类型
string 类型是 C++ 风格的字符串,它对 OI 选手更加友好,速度与字符数组基本持平,且不需要提前制定数组大小。但是当你需要卡常数的时候,string 类型动态分配内存的特性很可能会带来比较大的常数。
string str; // 定义一个空的字符串
string str("Hello, world"); // 定义一个 str 为 Hello, world
string str(n, 'h'); // 定义 str 为 n 个 h
注意,string 类型不以 \0 结尾。
string 类型的输出输入可以使用 cin, cout,或者可以自定义输入/输出函数。当使用 cin 函数读取字符串的时候,注意遇到空格或者换行符就会停止。string 类型的长度可以认为是任意长度的,前提是不超过计算机的内存限制。
有时,程序需要读取一行字符串(包括空格),那么可以使用 C++ 提供的 getline() 函数,可以使用 getline(cin, str) 读取一行字符串到 str 里。
string 类型可以方便的进行字符串的拼接,如 str = str1 + str2,此时 str 就为 str1 在前、str2 在后的一个字符串,注意,其中 str1 和 str2 至少有一个是 string 类型,str = "ni" + "hao" 这种写法是会编译错误的。
字符串的长度
对于 C 风格字符串,可以使用 strlen(str) 来获取字符串的长度。但是注意,这种方法的时间复杂度根据编译器的优化而定,最差为 \(O(n)\)。请不要在正式比赛中把你的命运交给编译器决定。
对于 C++ 风格的字符串,可以使用 str.length() 或 str.size() 来获取字符串的长度,这两种方法都是 \(O(1)\)。
字符串比较
字符串的比较基于字典序,字符串的字典序是指,以第 \(i\) 个字符作为第 \(i\) 关键字进行大小比较,空字符小于字符集内任何字符。
C 风格的字符串可以使用 strcmp(str1, str2) 函数来比较 str1, str2 两个字符串的大小关系,若 \(\text{str1}=\text{str2}\),那么返回 \(0\),如果 \(\text{str1}<\text{str2}\) 返回负数,否则返回正数。
对于 C++ 风格的字符串,可以直接使用 > >= < <= == 等运算符进行比较,也可以使用 str1.compare(str2) 这样的方式来比较,返回值的含义与 strcmp() 函数一样。
习题
例题1 生日相同
在一个大班级中,存在两个人生日相同的概率非常大,现给出每个学生的名字,出生月日。试找出所有生日相同的学生,\(1\le n\le 10^5\)。
简单题,由于最多只有 \(12\times 31=372\) 个日子,直接开 vector 存下每个生日对应着谁即可。
vector<string> y[13][32];
string str;
int n, mm, dd;
bool cmp(string a, string b) {
if (a.size() == b.size()) return a < b;
else return a.size() < b.size();
}
int main(void) {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> str >> mm >> dd;
y[mm][dd].push_back(str);
}
for (int i = 1; i <= 12; ++i) { //枚举月
for (int j = 1; j <= 31; ++j) { //枚举日
if (y[i][j].size() > 1) {
sort(y[i][j].begin(), y[i][j].end(), cmp);
cout << i << ' ' << j << ' ';
for (string s : y[i][j])
cout << s << ' ';
cout << endl;
}
}
}
return 0;
}
例题2 生日排序
给出 \(n\) 个人的生日,要求按照生日大到小的顺序依次输出名称。对于生日相同的两个人,按照字典序从大到小排序。
字典序裸题,自定义一个 cmp 比较函数即可。
struct PERSON{
int yyyy, mm, dd;
string name;
bool operator < (const PERSON b) const {
if (yyyy != b.yyyy) return yyyy < b.yyyy;
if (mm != b.mm) return mm < b.mm;
if (dd != b.dd) return dd < b.dd;
return name > b.name;
}
} a[105];
int n;
int main(void) {
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i].name >> a[i].yyyy >> a[i].mm >> a[i].dd;
sort(a + 1, a + 1 + n);
for (int i = 1; i <= n; ++i)
cout << a[i].name << endl;
return 0;
}
第二章 哈希
本章的代码量较大,许多代码都是 @SSL_ZZL 大佬写的。在这里谢谢这位大佬。
例题1 出现次数
给定两个字符串 \(x,y\),问 \(x\) 在 \(y\) 中出现了多少次,\(1\le |x|,|y| \le 10^6\)。
设 \(|x|=n,|y|=m\)。那么我们可以枚举 \(i\),判断 \(y[i\cdots (i+m-1)]\) 是否等于 \(x\)。可是这样的时间复杂度为 \(O(nm)\),无法接受。
考虑优化,我们发现,如果能找到一个快速判断两个字符串是否相等的方法,就能将时间复杂度优化为 \(O(n)\)。如何优化?这里就要引入一个新算法,字符串哈希。
定义
字符串哈希的作用就是,把一个字符串映射到一个整数,并且这个整数可以被方便的表示出来。
我们定义一个函数把字符串映射到整数的函数 \(f\),称之为哈希函数。具体来说,我们希望 \(f\) 实现以下功能:
-
当输入的字符串 \(s\) 不同时,\(f(s)\) 也互不相同。
-
当输入的 \(s\) 相同时,\(f(s)\) 始终相同。
但是,由于字符串的个数远大于可以被方便表示出的整数的个数,所以我们退一步讲,希望第一条尽可能成立。当输入的 \(s\) 不同、返回的 \(f(s)\) 却相同的情况,我们称之为哈希碰撞。
这里估计已经有读者想到,对于任意一个只包含小写字母的字符串 \(s\),其相当于一个 \(26\) 进制数。于是,我们可以把这个 \(26\) 进制数转换为一个 \(10\) 进制数,返回这个 \(10\) 进制数。
这种方法很好,也有效的从根本上杜绝了哈希碰撞的可能。但是 long long 的表示范围为 \(2^{63} \approx 10^{19}\),而 \(26^{14} \approx 7\times 10^{19}\),也就是说,如果使用上述方法,最大也就能表示一个长度为 \(13\) 的字符串。
问题的根本在于,当 \(n\ge 14\) 的时候,返回的 \(f(s)\) 的值会过大。所以我们只需要 \(f(s)\) 保持在一个可以接受的范围即可。对于这种需求,可以将最后的返回值 \(\bmod M\),其中 \(M\) 是一个大数。
也就是说,我们可以令 \(f(s) = b^{n-1}s_1 + b^{n-2}s_2 + \cdots + s_n\)。我们约定,令 \(f_i(s) = f(s[1\cdots i])\),那么有 \(f_i(s) = f_{i-1}(s) \times b + s_i\)
那么,我们现在可以 \(O(n)\) 的求出一个字符串的前缀 Hash,那么如何在 \(O(1)\) 的时间内求出字符串的某一个字串的哈希值呢?
若我们要求出 \(f(s[l\cdots l+k])\),根据上面的定义,也就是 \(b^{k-1}s_l + b^{k-2}s_{l+1} + \cdots + s_{l+k}\)。
观察一下这个式子,考虑如何用前缀哈希表示出来,发现有如下式子。
改进
发现若使用这种哈希方法,当 \(M=10^9+7\),碰撞率 \(\dfrac 1M\),那么当 \(n=10^6\),碰撞率就高达 \(\dfrac 1{1000}\)。这个碰撞率显然在 OI 中是致命的。所以我们需要将碰撞率降低。我们可以另外再选择一个素数 \(P\),定义一个字符串的哈希值 1 为 \(f(s) \bmod M\),哈希值 2 为 \(f(s) \bmod P\)。这样我们成功将碰撞率降低到了 \(\dfrac1{M\times P}\)。
回到上面的问题。
给定两个字符串 \(x,y\),问 \(x\) 在 \(y\) 中出现了多少次,\(1\le |x|,|y| \le 10^6\)。
如何解决这个问题?首先求出 \(f(x)\),接下来枚举 \(i\),判断 \(f(y[i\cdots i+|x|])\) 是否等于 \(x\) 即可。由于这里计算哈希值为 \(O(1)\) 的,总时间复杂度为 \(O(n+m)\)。
typedef unsigned long long ull;
const int MAXN = 1e6 + 5;
ull f[MAXN], n, m, b = 256, xhash, bpow = 0;
char x[MAXN], y[MAXN];
int main(void) {
scanf("%s %s", x + 1, y + 1);
n = strlen(x + 1), m = strlen(y + 1);
for (int i = 1; i <= m; ++i) // 处理出前缀哈希值
f[i] = f[i - 1] * b + y[i]; // 由于 f 是 Unsigned long long 所以相当于自然 mod 2^64
bpow = 1;
for (int i = n; i >= 1; --i)
{xhash += x[i] * bpow; bpow *= b;}
int ans = 0;
for (int i = 0; i <= m - n; ++i)
if (xhash == f[i + n] - f[i] * bpow)
++ans;
printf("%d\n", ans);
return 0;
}
例题2 字符串哈希
给定 \(n\;(1\le n\le 10^4)\) 个字符串(第 \(i\) 个字符串长度为 \(m_i\;(m_i\approx 1000)\),字符串内包含数字、大小写英文字母),请求出 \(n\) 个字符串中共有多少个不同的字符串。
简单题。只需要要 \(O(nm)\) 计算每个字符串的哈希值,然后判断即可。
string s, hash[P + 10];
int n, ans;
bool demo(string s) {
int sum = 0;
for (int i = 0; i < s.size(); i++)
sum = (sum * 123 + s[i]) % P; //算出字符串的hash值
int seat = 0;
while (hash[(sum + seat) % P] != "" && hash[(sum + seat) % P] != s) //寻找hash值的位置
seat++;
if (hash[(sum + seat) % P] == "") { //没有出现过,将hash值放进hash表里
hash[(sum + seat) % P] = s;
return 1;
}
return 0;
}
int main(void) {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
cin >> s;
if (demo(s))
ans++;
}
printf("%d", ans);
}
例题3 回文子串
给定一个长度为 \(n\;(n\le 10^6)\) 的字符串 \(s\),求他的最长回文子串的长度是多少。有多组数据,\(T\le 30\)。
思考:如何判断一个字符串是否为一个回文串?设字符串 \(s\) 的中心为 \(k\),长度为 \(n\),那么当且仅当 \(f(s[1\cdots k])=f(s[k\cdots n])\) 的时候,\(s\) 为一个回文串。
考虑枚举中点 \(p\),在 \(p\) 确定的情况下,我们想知道,使得 \(s[p-k \cdots p] = s[p\cdots p+k]\) 的 \(k\) 最大是多少。
自然可以暴力枚举一个 \(k\)。可是这样的做法是 \(O(n^2)\),会超时。考虑能不能将这个寻找 \(k\) 的过程压缩到 \(O(n)\) 以下。
观察一下,发现 \(k\) 具有单调性:即若 \(k_1\le k_2\),而 \(s[p-k_1 \cdots p] \ne s[p\cdots p+k_1]\),那么 \(k_2\) 也肯定不能使 \(s[p-k_2 \cdots p] = s[p\cdots p+k_2]\)。
所以我们可以二分 \(k\),将寻找 \(k\) 的时间复杂度降到 \(O(\log n)\)。
总时间复杂度:\(O(n\log n)\)。
typedef unsigned long long ull;
ull p = 131;
ull a[1000010], base[1000010], b[1000010];
int n, ans, cnt;
string s;
bool check()
{
if (s[0] == 'E' && s[1] == 'N' && s[2] == 'D')
return 1;
return 0;
}
void hash()
{
memset(base, 0, sizeof(base));
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
base[0] = 1ull;
for (int i = 0; i < n; i++)
{
base[i + 1] = base[i] * p;
a[i + 1] = a[i] * p + (s[i] - 'a'); //正序字符串哈希
}
for (int i = n - 1; i >= 0; i--)
b[i + 1] = b[i + 2] * p + (s[i] - 'a'); //倒序字符串哈希
}
void work()
{
for (int i = 1; i <= n; i++)
{ //找中心
int mid = 0, l = 0, r = n;
while (l <= r)
{ //长度奇数
mid = (l + r) >> 1;
if (i - mid < 1 || i + mid > n)
{
r = mid - 1;
continue;
}
if (a[i] - a[i - mid - 1] * base[mid + 1] == b[i] - b[i + mid + 1] * base[mid + 1])
{
ans = max(ans, mid * 2 + 1);
l = mid + 1;
}
else
r = mid - 1;
}
mid = 0, l = 0, r = n;
while (l <= r)
{ //长度偶数
mid = (l + r) >> 1;
if (i - mid + 1 < 1 || i + mid > n)
{
r = mid - 1;
continue;
}
if (a[i] - a[i - mid] * base[mid] == b[i + 1] - b[i + mid + 1] * base[mid])
{
ans = max(ans, mid * 2);
l = mid + 1;
}
else
r = mid - 1;
}
}
}
int main()
{
cin >> s;
n = s.size();
while (!check())
{
cnt++;
ans = 1;
hash();
work();
printf("Case %d: %d\n", cnt, ans);
cin >> s;
n = s.size();
}
}
例题4 对称正方形
给定一个 \(n\;(n \le 10^3)\) 行 \(m\;(m\le 10^3)\) 列的矩阵。求矩阵中上下对称且左右对称的正方形子矩阵的个数。
二维哈希。不过多解释,因为算法部分与基本一致。直接上代码。
typedef unsigned long long ull;
ull p1 = 131, p2 = 313;
ull g[1010][1010], xturn[1010][1010], yturn[1010][1010];
int ans, n, m, a[1010][1010];
struct c {
ull x, y;
} base[1010];
void yu() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) xturn[n - i + 1][j] = yturn[i][m - j + 1] = a[i][j];
}
}
void hash() //二维Hash
{
base[0].x = 1, base[0].y = 1;
for (int i = 1; i <= max(n, m); i++) {
base[i].x = base[i - 1].x * p1;
base[i].y = base[i - 1].y * p2;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
a[i][j] += a[i - 1][j] * p1;
xturn[i][j] += xturn[i - 1][j] * p1;
yturn[i][j] += yturn[i - 1][j] * p1;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
a[i][j] += a[i][j - 1] * p2;
xturn[i][j] += xturn[i][j - 1] * p2;
yturn[i][j] += yturn[i][j - 1] * p2;
}
}
}
bool check(int x, int y, int len) {
int v1, v2, v3, y1, x1;
if (x < len || x > n || y < len || y > m)
return 0;
v1 = a[x][y] - a[x - len][y] * base[len].x - a[x][y - len] * base[len].y +
a[x - len][y - len] * base[len].y * base[len].x;
x1 = n - (x - len); //上下翻转
v2 = xturn[x1][y] - xturn[x1 - len][y] * base[len].x - xturn[x1][y - len] * base[len].y +
xturn[x1 - len][y - len] * base[len].y * base[len].x;
y1 = m - (y - len); //左右翻转
v3 = yturn[x][y1] - yturn[x - len][y1] * base[len].x - yturn[x][y1 - len] * base[len].y +
yturn[x - len][y1 - len] * base[len].y * base[len].x;
if (v1 == v2 && v2 == v3)
return 1;
else
return 0;
}
void work() {
int t = 0, l = 0, r = max(n, m) + 1, mid = 0, x, y;
//长度为奇数
for (int i = 1; i < n; i++) { //枚举中心点
for (int j = 1; j < m; j++) {
t = 0, l = 0, r = max(n, m) + 1, mid = 0;
while (l < r) { //二分边长
mid = (l + r + 1) >> 1;
x = mid + i, y = mid + j; //右下角
if (check(x, y, mid * 2)) {
t = mid;
l = mid;
} else
r = mid - 1;
}
ans += t;
}
}
//长度为奇数
for (int i = 1; i <= n; i++) { //枚举中心点
for (int j = 1; j <= m; j++) {
t = 0, l = 0, r = max(n, m) + 1, mid = 0;
while (l < r) {
mid = (l + r + 1) >> 1; //二分边长
x = mid + i, y = mid + j; //右下角
if (check(x, y, mid * 2 + 1)) {
t = mid;
l = mid;
} else
r = mid - 1;
}
ans += t;
}
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) scanf("%d", &a[i][j]);
yu();
hash();
work();
ans += m * n;
printf("%d", ans);
}
例题5 单词背诵
灵梦有 \(n\;(n\le 10^3)\) 个单词想要背,文章由 \(m\;(m\le 10^5)\) 个单词构成,她想在文章中找出连续的一段,其中包含最多的她想要背的单词(重复的只算一个)。在背诵的单词量尽量多的情况下,使选出的文章段落尽量短。
你需要求出 文章中最多包含的要背的单词数 与 文章中包含最多要背单词的最短的连续段的长度。
首先第一个问题很好解决,直接排序后二分查找每个想背的单词是否出现即可。
第二个问题需要用到双指针 (two-pointers) 法。对于一个首先令 \(l=r=1\),然后让 \(r\) 逐步向右扩大。每次当 \(l\cdots r\) 之间包含了所有单词的时候,并让 \(l\) 逐步往右扩大,直到 \(l\cdots r\) 之间不再包含所有单词时,记录下移动前的 \(r-l+1\) 的值。最后取 \(r-l+1\) 的最小值即可。
struct DT {
int num;
ull s;
} hash[1010];
int n, m, ans1, wdn, ans2, r, atcp[100010], v[1010];
string con, atc;
ull atcs;
bool cmp(const DT& k, const DT& l) { return k.s < l.s; };
int find(ull s) { //二分查找单词编号
int l = 1, r = n, mid;
while (l <= r) {
mid = (l + r) / 2;
if (hash[mid].s < s)
l = mid + 1;
else if (hash[mid].s > s)
r = mid - 1;
else
return hash[mid].num;
}
return -1;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
cin >> con;
hash[i].num = i; //每个单词的标号
for (int j = 0; j < con.size(); j++) hash[i].s = hash[i].s * 131ull + (con[j] - 'a' + 1); // hash处理
}
sort(hash + 1, hash + 1 + n, cmp); //以hash值排序
scanf("%d", &m);
for (int i = 1; i <= m; i++) {
cin >> atc;
atcs = 0;
for (int j = 0; j < atc.size(); j++) atcs = atcs * 131ull + (atc[j] - 'a' + 1);
int pit = find(atcs); // pit就是当前文章中的单词是背诵单词中的哪一个编号
if (pit > 0) { //当前单词需背诵
if (!v[pit])
ans1++;
++v[pit];
}
atcp[i] = pit; //记录编号
}
memset(v, 0, sizeof(v)); //记录单词在l~r中出现次数
r = 1, ans2 = 2147483647;
for (int l = 1; l <= m; l++) { //枚举左边界
while (wdn < ans1 && r <= m) { //直到找到所有要背的单词 或 r出界了
if (atcp[r] >= 0) { //有编号(单词需背)
if (v[atcp[r]] == 0)
wdn++; //第一次出现记录答案
++v[atcp[r]]; //当前单词出现次数累计
}
r++;
}
if (wdn == ans1) //找到了所有要背的单词
ans2 = min(ans2, r - l); //取最短的长度
if (atcp[l] >= 0) { //对l位置上的单词做处理,r就不需要重新从l开始更新了
--v[atcp[l]]; // l位置上的单词 的出现次数-1
if (!v[atcp[l]])
wdn--;
//如果这个位置上的单词是l~r中只出现过一次,那么l向右枚举时,l~r中将没有这个词,答案-1
}
}
printf("%d\n%d", ans1, ans2);
}
习题
习题1 子正方形
给出两个 \(n\times n\;(1\le n\le 50)\) 的正整数矩阵,求这两个矩阵的最大公共子正方形矩阵的边长。
习题2 特殊数列
有一个数列 \(a\),\(a_0=1\),\(a_{i+1}=(A\times a_i + a_i \bmod B) \bmod C\;(-10^9\le A,B,C \le 10^9)\),要求这个数列第一次出现重复的项的标号。
习题3 求好元素
如果在一个由 \(n (1\le n\le 5000)\) 个整数组成的数列 \(a\) 中,存在 \(a_m+a_n+a_p=a_i\;(1\le n,m,p < i)\)(\(n,m,p\) 可以相同)的话,\(a_i\) 就是一个“好元素”。问“好元素”的个数。
习题4 上课点名
一个老师喜欢上课前先点名,小明发现自己被点到了两次,于是小明开始质疑老师的点名是否有重复或误报为其他班同学。当然小明可不想一个个比较,所以他把这个任务交给了你,小明会提供班上人数 \(n\;(1\le n\le 10^4)\) 和他们的名字,同时小明也会记下老师报的名字与他们的个数 \(m\;(1\le m\le 5\times 10^5)\)。
习题5 最大分离度
对于任意两人,他们的分离度是联系两个人需要经过的最小的关系数。对于一个关系网络,最大分离度是网络中任意两个的分离度的最大值。如果一个网络有两个人没有通过关系链连接起来,这个网络是不连通的。请你判断一个网络是否联通。
数据范围:人数 \(P\le 50\),关系数 \(R\le P^2\)。
习题6 回文分区
给出一个只包含小写字母字符串 \(s\),长度为 \(n\;(1\le n\le 10^6)\),要求你将它划分成尽可能多的小块,使得这些小块构成回文串。多组数据,数据数 \(T\le 10\)。
第三章 字符串匹配 (KMP Algorithm)
由于网络上相同内容很多,本章的内容可以前往 OI-Wiki 上查看。
第四章 字典树
定义
字典树 Trie 是一个可以很方便的处理字符串问题的数据结构。将若干个字符串建成一颗字典树,其中的每个节点代表从根走到当前位置的一个字符子串。
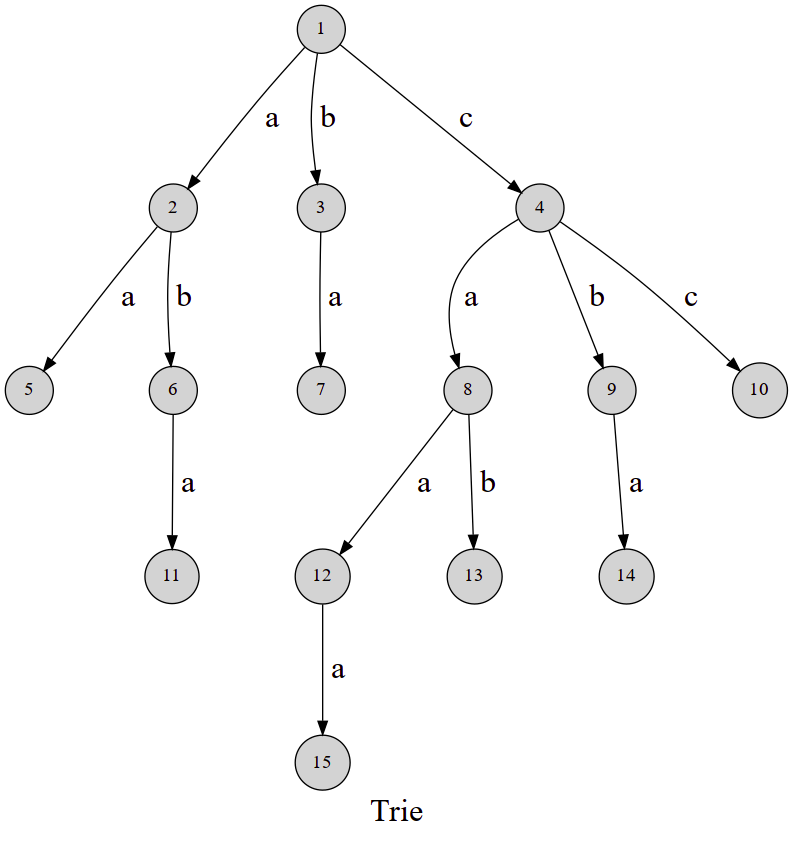
如图,这就是一棵字典树,其中这条 \(1\to 2 \to 5\) 的路径表示了一个字符串 \(\text{aa}\),而路径 \(1\to 4\to 8\to 12\to 15\) 这条路径表示了字符串 \(\text{caaa}\)。
trie 的结构非常好懂,我们用 \(\delta(u,c)\) 表示结点 \(u\) 的 \(c\) 字符指向的下一个结点,或着说是结点 \(u\) 代表的字符串后面添加一个字符 \(c\) 形成的字符串的结点。(\(c\) 的取值范围和字符集大小有关,不一定是 \(0\sim 26\)。)
有时需要标记插入进 trie 的是哪些字符串,每次插入完成时在这个字符串所代表的节点处打上标记即可。
字典树的实现非常简单,如下,就是一个封装好的字典树。
// C++ Version
struct trie {
int nex[100000][26], cnt;
bool exist[100000]; // 该结点结尾的字符串是否存在
void insert(char *s, int l) { // 插入字符串
int p = 0;
for (int i = 0; i < l; i++) {
int c = s[i] - 'a';
if (!nex[p][c])
nex[p][c] = ++cnt; // 如果没有,就添加结点
p = nex[p][c];
}
exist[p] = 1;
}
bool find(char *s, int l) { // 查找字符串
int p = 0;
for (int i = 0; i < l; i++) {
int c = s[i] - 'a';
if (!nex[p][c])
return 0;
p = nex[p][c];
}
return exist[p];
}
};
例题1 前缀统计
给定 \(n(n\le 10^6)\) 个字符串 \(s_1,s_2,\cdots,s_n\),接下来进行 \(m\) 次询问,每次询问给定一个字符串 \(t\),求 \(s_1\sim s_n\) 中有多少个字符串是 \(t\) 的前缀。
这个题目似乎是字典树的模板题,我们只需要先将这 \(n\) 个字符串插入字典树,然后对于每一个 \(t\),查询路径上有多少个结束标记即可。
#include <cstdio>
#include <cstring>
using namespace std;
const int MAXN = 1e6 + 5, MAXL = 26;
struct Trie {
int nex[MAXN][MAXL], cnt, exist[MAXN];
void insert(char *s, int len) {
int p = 0;
for (int i = 0; i < len; ++i) {
int q = s[i] - 'a';
if (nex[p][q] == 0) nex[p][q] = ++cnt;
p = nex[p][q];
}
exist[p]++;
}
int query(char *t, int len) {
int p = 0, ret = 0;
for (int i = 0; i < len; ++i) {
int q = t[i] - 'a';
if (nex[p][q] == 0) break;
p = nex[p][q];
ret += exist[p];
}
return ret; // t 为某个 s 的前缀,注意有可能 s = t
}
} T;
char s[MAXN], t[MAXN];
int main(void) {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
scanf("%s", s);
T.insert(s, strlen(s));
}
while (m--) {
scanf("%s", t);
printf("%d\n", T.query(t, strlen(t)));
}
return 0;
}
例题2 最大异或对
给定的 \(n(n\le 10^5)\) 个整数 \(a_1,a_2,\cdots,a_n(a_i< 2^{31})\),选出两个数进行 xor(异或)运算,求得到的结果的最大值。
本题需要学习字典树的一种特殊形式,01Trie。为什么说这是一种特殊的字典树?因为 01Trie 是一棵储存 0/1 字符串的字典树。
那他与本题有什么关系?我们知道,高位的数字大的数字越大,而不用考虑低位上的数字的大小。也就是说,我们有一种贪心策略,即优先使高位异或后的结果为 \(1\)。
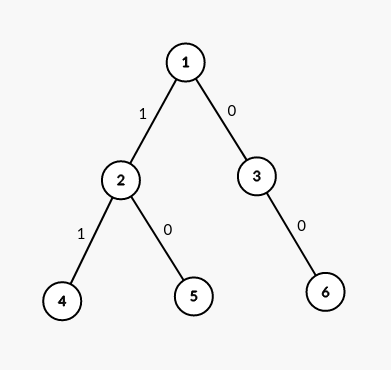
如上面这棵字典树,就是我们插入了三个 0/1 串(\(00,10,11\))的结果。如果此时我们要查询这三个串中与 \(01\) 异或最大的值,我们可以这样做。
首先令指针 \(p=1\),发现 \(01\) 的第一位为 \(0\),也就是我们第一位要尽量往 \(1\) 走。我们发现节点 \(1\) 有这条 \(1\) 边,所以令 \(p=2\)。同理,接下来应该往 \(0\) 走,所以令 \(p=5\)。
那么本题的做法显然,首先将 \(n\) 个字符串插入 01Trie 中,接下来对于每个字符串 \(s\),我们查找一个尽量大的异或值,最后取最大值即可。
注意在本题中,有可能这些 01 字符串的长度不一样,我们只需要高位补 0 即可,如上。
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int MAXN = 1e7 + 5, MAXL = 4;
struct Trie {
int nex[MAXN][MAXL], cnt, exist[MAXN];
void insert(int x) {
int p = 0;
for (int i = 30; i >= 0; --i) { //题目保证了x<2^31,所以可以直接强制把所有字符串都补到30位
int q = (x >> i) & 1; //取出x的第i位
if (nex[p][q] == 0) nex[p][q] = ++cnt;
p = nex[p][q];
}
}
int query(int x) {
int p = 0, ret = 0;
for (int i = 30; i >= 0; --i) {
int q = (x >> i) & 1;
if (nex[p][!q]) {
ret += (1 << i);
q = !q;
}
p = nex[p][q];
}
return ret;
}
} T;
int n, a[MAXN];
int main(void) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
T.insert(a[i]);
}
int ans = 0;
for (int i = 1; i <= n; ++i) {
ans = max(ans, T.query(a[i]));
}
printf("%d", ans);
return 0;
}
例题3 最长异或路径
给定 \(n(n\le 10^5)\) 个节点的树,每个节点有一个权值 \(w(w<2^{31})\),求出一条路径,使得在这条路径上的所有点的权值异或最大。
本题和上一题有点相像。本题需要使用到树上差分的思想。那么,树上差分的思想是什么呢?我们知道,异或有个奇妙的性质,即 \(a \oplus a = 0, a \oplus 0 = a\),这意味着,异或具有反运算,且异或的反运算为他自己。
知道了这个性质,我们就可以做出这道题目了,我们设 \(f(x,y)\) 表示 \(x\to y\) 路径上的异或值,那么显然有 \(f(x,y)=f(x,\operatorname{LCA}(x,y)) \oplus f(\operatorname{LCA}(x,y),y)\)。
那么,我们需要 \(\Theta(\log n)\)计算 \(\operatorname{LCA}\)吗?显然不用。因为我们提到了异或的另一个性质,也就异或的自反性。我们其实不需要知道 \(\operatorname{LCA}(x,y)\) 到底等于多少,因为设 \(\operatorname{LCA}(x,y)=p,\text{root}=r\),有如下公式。
也就是说,我们只需要 \(\forall 1\le i\le n, f(i,r)\) 即可,设 \(f(i,r)=d_i\),那么我们只需要找到两个 \(i,j\) 使得 \(d_i\oplus d_j\) 最大即可,这就回到了上面的问题,可以使用上面的方法解决。
#include <iostream>
#include <cstdio>
#include <iomanip>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
int n, k, s[3200010], trie[3200010][2], h[200010], tot = 1, u, v, w, ans;
struct c {
int x, next, w;
} a[200010];
void add(int x, int y, int w) {
k++;
a[k].x = y;
a[k].next = h[x];
a[k].w = w;
h[x] = k;
}
void dfs(int x, int fa) { //求出所有的s[i]
int v;
for (int i = h[x]; i; i = a[i].next) {
v = a[i].x;
if (v == fa) continue;
s[v] = s[x] ^ a[i].w;
dfs(v, x);
}
}
int get(int x) {
int p = 1, ans = 0, c;
for (int i = 31; i >= 0; i--) {
if (((x >> i) & 1) == 1) c = 0;
else c = 1;
if (trie[p][c]) ans += (1 << i);
else c = (x >> i) & 1;
p = trie[p][c];
}
return ans;
}
void insert(int x) {
int p = 1, c;
for (int i = 31; i >= 0; i--) {
c = (x >> i) & 1;
if (!trie[p][c]) trie[p][c] = ++tot;
p = trie[p][c];
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n - 1; i++) {
scanf("%d%d%d", &u, &v, &w);
add(u, v, w);
add(v, u, w);
}
dfs(1, 0);
//后面的就跟上一题(最大异或对)一样了
for (int i = 1; i <= n; i++) insert(s[i]);
for (int i = 1; i <= n; i++) ans = max(ans, get(s[i]));
printf("%d", ans);
}
例题4 阅读理解
有 \(n(1\le 10^3)\) 篇阅读理解,每篇有许多生词,指定一个生词 \(s\),询问 \(s\) 在哪些阅读理解里出现。
对于每一个生词 \(s\),往包含他的阅读理解建条边。
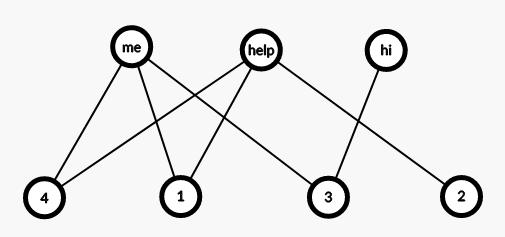
查询的时候直接输出即可。
#include <iostream>
#include <map>
#include <vector>
using namespace std;
map<string, vector<int>> a;
int n, m, l;
string s;
int main(void) {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> l;
for (int j = 1; j <= l; ++j) {
cin >> s;
if (a[s].size() == 0 || a[s][a[s].size() - 1] != i)
a[s].push_back(i);
}
}
cin >> m;
for (int i = 1; i <= m; ++i) {
cin >> s;
for (auto x : a[s]) {
cout << x << ' ';
}
cout << endl;
}
return 0;
}
例题5 单词拼接
给定由一些单词组成的词典,单词数 \(\le 5\times 10^3\)。一个单词是特殊的,当且仅当它能由词典里的两个单词拼接而成。求词典里特殊的单词数。
我们知道,若一个字符串 \(a\) 为特殊的字符串,那么我们必定能找到两个字符串 \(s,t\),\(s\) 为 \(a\) 的前缀且 \(t\) 为 \(a\) 的后缀,并且 \(|s|+|t| = |a|\)。
我们发现,若设 \(\operatorname{rev}(a) = r\),那么 \(t\) 为 \(a\) 的后缀也就相当于是 \(r\) 的前缀。
这样,我们就将原先的判定操作转换成了两个前缀的判定操作,而我们知道,字典树可以很方便的进行这个操作,所以我们可以使用字典树来优化这个操作。
时间复杂度 \(\Theta(n^2 \operatorname{strlen}(s))\)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f, N = 50010;
int n, tot = 1;
char s[N][33];
int trie[N << 5][30], ans, ed[N << 5];
void insert(int id) {
int p = 1, len = strlen(s[id] + 1);
for (int i = 1; i <= len; i++) {
int ch = s[id][i] - 'a';
if (!trie[p][ch])
trie[p][ch] = ++tot;
p = trie[p][ch];
}
ed[p]++;
}
int find(int id, int l, int r) {
int p = 1;
for (int i = l; i <= r; i++) {
int ch = s[id][i] - 'a';
if (!trie[p][ch])
return 0;
p = trie[p][ch];
}
return ed[p];
}
int main() {
int now = 1;
while (scanf("%s", s[now] + 1) != EOF) {
insert(now);
now++;
}
for (int i = 1; i <= now - 1; i++) {
int len = strlen(s[i] + 1);
for (int k = 1; k < len; k++)
if (find(i, 1, k) && find(i, k + 1, len)) {
printf("%s\n", s[i] + 1);
break;
}
}
return 0;
}
例题6 最短前缀
有 \(n(n\le 10^3)\) 个单词,保证互不相同,对于每个单词 \(s\) 寻找 \(s\) 的一个前缀 \(p\) 使得 \(p\) 在这 \(n\) 个单词中仅为 \(s\) 的前缀。
这个题目也是比较简单的题目,建出这 \(n\) 个单词的字典树,对于每个单词 \(s\) 遍历一遍这个字典树,若发现从当前节点往下没有任何分支了,那么说明到现在的字符串肯定为一个独一无二的前缀了。
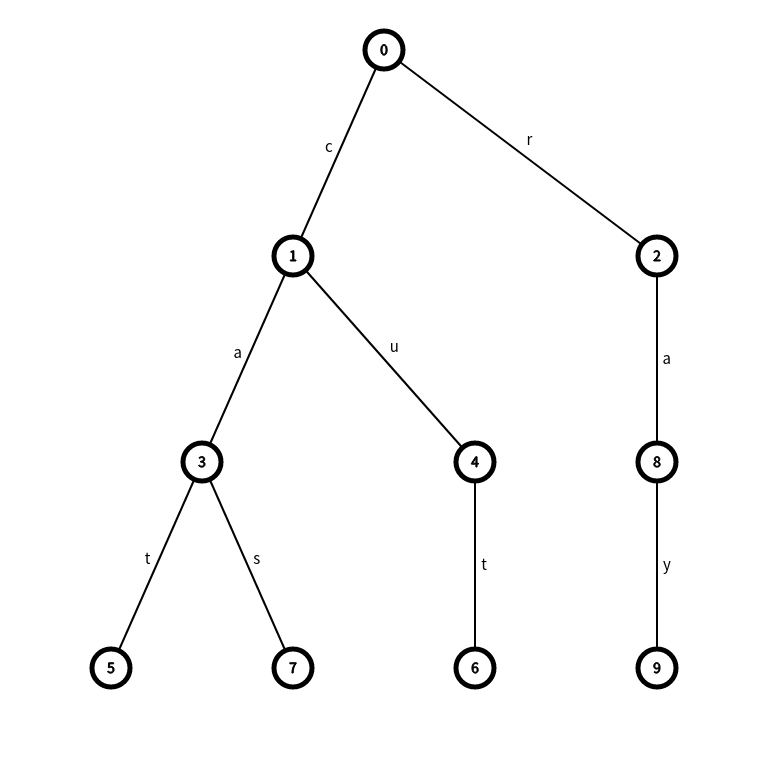
如上面这个字典树,若我们想找到 \(\text{cat}\) 的最长独立前缀,我们从 \(0\) 节点开始遍历:
- 进入 \(1\) 节点,\(\text{ans = c}\);
- 发现 \(1\) 节点儿子数大于 \(1\),\(\text{ans = ca}\);
- 进入 \(3\) 节点。
- 发现节点 \(3\) 儿子数大于 \(1\),\(\text{ans = cat}\);
- 进入节点 \(5\)。
- 发现节点 \(5\) 为叶子节点,\(\text{ans = cat}\)。
#define mod 1000000007
#define eps 1e-6
#define ll long long
#define INF 0x3f3f3f3f
#define ME0(x) memset(x, 0, sizeof(x))
using namespace std;
string s[1005];
int main() {
int n = 0;
while (cin >> s[++n]);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= s[i].size(); ++j) {
string ss = s[i].substr(0, j);
int flag = 1;
for (int k = 1; k <= n; ++k) {
if (k != i && s[k].substr(0, j) == ss) {
flag = 0;
break;
}
}
if (flag || j == s[i].size()) {
cout << s[i] << " " << ss << endl;
break;
}
}
}
}
例题7 lowbit 求和
给定长度为 \(n(n\le 10^5)\) 的序列 \(a(a_i\le 2^{60}-1)\),求 \(\sum^n_{i=1}\sum^n_{j=1}\operatorname{lowbit}(a_i~\operatorname{xor}a_j)\)。
我们知道,\(\operatorname{lowbit}(x)\) 表示 \(x\) 的最后一位 \(1\) 所对应的值。建一棵 01Trie 即可。
#include <iostream>
#include <cstdio>
using namespace std;
unsigned long long mod = 199907210507;
long long n, tot = 1ll;
long long a[6010101];
long long trie[6010101][2], b[60101010];
void add(long long x) {
long long now = 1;
for (int i = 0; i <= 61ll; i++) {
int j = (x >> i) & 1ll;
if (!trie[now][j])
trie[now][j] = ++tot;
now = trie[now][j];
b[now]++;
}
}
unsigned long long query(long long x) {
unsigned long long sum = 0;
long long now = 1;
for (int i = 0; i <= 61; i++) {
int j = (x >> i) & 1;
if (trie[now][j ^ 1])
sum = (sum + b[trie[now][j ^ 1]] % mod * (1ll << i) % mod) % mod;
now = trie[now][j];
}
return sum;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
add(a[i]);
}
unsigned long long ans = 0;
for (int i = 1; i <= n; i++) ans = (ans + query(a[i])) % mod;
cout << ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号