线性DP
# 线性DP
所有例题链接:https://ac.nowcoder.com/acm/contest/1041
例题1:POJ2279
思考:
考虑 \(dp_{i,j,k}\) 表示第 \(i\) 行,第 \(j\) 列,安排 \(k\) 去站的方案数。
错误原因:
安排 \(k\) 去站但是可能会造成重复选择 \(k\) 。
正解:
考虑 \(dp_{a1,a2,a3,a4,a5}\) 表示各排从左边起分别站了 \(a1,a2,a3,a4,a5\) 个人时,合影方案数。
疑惑:
Q1.为什么不用考虑某个位置究竟站的是谁?
Q2.怎样确定这个问题是无后效性的?
Q3.怎样确定这个问题具有最优子结构?
自我解答:
A1.题目要求每一列单调并且每一排单调,对于第一个位置,也就是最高的肯定站在第一个位置,但是对于第二高的就有两个选择 (如果在第二排可以站人的情况下) ,第二个人的站位也会影响之后的第三高的人的站位。其实在正解的 \(dp\) 状态设置上面,是有考虑到某个位置究竟站的是谁的,只是题目在于求方案数,而不是具体的方案情况。因此在实际的 \(dp\) 的含义上面是并没有考虑到某个位置究竟站的是谁,但在 \(dp\) 的状态转移过程中其实是有考虑到某个位置究竟站的是谁的。
A2.其实主要感觉和题目的本身有关系?因为在题目本身的操作中,其实隐藏的操作过程是选一个人站在某个位置上面对于这个操作仅有的操作来说,是无后效性的,因此这个问题无后效性。
A3.最优子结构说的是下一阶段的最优解能够由前面各个阶段的最优解求解,考虑到当前的站位方案数其实与下一站位方案数息息相关因此这个问题具有最优子结构。
小结:
感觉这个线性DP和我之前所做的线性DP都不同,首先是 \(dp\) 的状态都定义到了我没想到的五维,这看起来既暴力又美观(暴力美学)。
《算法竞赛进阶指南》:
设计动态规划的状态转移方程,不一定要以“如何计算出一个状态”的形式给出,你也可以考虑”一个已知状态应该更新哪些后续阶段的位置状态“。
收获:
1.对 无后效性 和 最优子结构 有了更深的认识。
2.对 DP状态的定义 的定义又多了一种认识。(以后要更大胆一点,之前一直觉得三维基本上都顶天难度了)
3.”状态“ ”阶段“ ”决策“ 动态规划的三要素。
4.”子问题重叠“ ”无后效性“ ”最优子结构“ 动态规划的三个基本条件。
自己之前对线性DP的一些求解流程:
1.读懂题。
2.根据题目的数据范围和求解对象定义DP的含义 即 \(dp_{i,j}\) 表示什么?
3.初始条件 和 答案确定。
4.写状态转移方程。
5.确定枚举顺序 和 限制条件。
6.写程序 AC。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN = 6;
ll Tex = 1, n, a[MAXN];
void AC()
{
while(cin >> n && n)
{
memset(a, 0, sizeof a);
for(int i = 1; i <= n; i ++)
cin >> a[i];
ll dp[a[1] + 1][a[2] + 1][a[3] + 1][a[4] + 1][a[5] + 1];
memset(dp, 0, sizeof dp);
dp[0][0][0][0][0] = 1;
for(int a1 = 0; a1 <= a[1]; a1 ++)
{
for(int a2 = 0; a2 <= a[2]; a2 ++)
{
for(int a3 = 0; a3 <= a[3]; a3 ++)
{
for(int a4 = 0; a4 <= a[4]; a4 ++)
{
for(int a5 = 0; a5 <= a[5]; a5 ++)
{
if(a1 < a[1])
dp[a1 + 1][a2][a3][a4][a5] += dp[a1][a2][a3][a4][a5];
if(a1 > a2 && a2 < a[2])
dp[a1][a2 + 1][a3][a4][a5] += dp[a1][a2][a3][a4][a5];
if(a1 > a3 && a2 > a3 && a3 < a[3])
dp[a1][a2][a3 + 1][a4][a5] += dp[a1][a2][a3][a4][a5];
if(a1 > a4 && a2 > a4 && a3 > a4 && a4 < a[4])
dp[a1][a2][a3][a4 + 1][a5] += dp[a1][a2][a3][a4][a5];
if(a1 > a5 && a2 > a5 && a3 > a5 && a4 > a5 && a5 < a[5])
dp[a1][a2][a3][a4][a5 + 1] += dp[a1][a2][a3][a4][a5];
}
}
}
}
}
cout << dp[a[1]][a[2]][a[3]][a[4]][a[5]] << endl;
}
}
int main()
{
ios::sync_with_stdio(false);
// cin >> Tex;
while(Tex --) AC();
return 0;
}
例题2:LCIS(最长公共上升子序列)
思考:
这个题是 LIS 和 LCS 的综合,于是不难想到定义 \(dp_{i,j}\) 表示 \(A_{1}\) ~ \(A_{i}\) 与 \(B_{i}\) ~ \(B_{j}\) 可以构成以 \(B_{j}\) 结尾的 LCIS 的最大长度。
状态转移方程:
\(if \quad a_{i} \neq b_{j} \quad dp_{i,j} = dp_{i - 1, j}\)
\(else \quad dp_{i, j} = \max_{0 \le k < j, b_{k} > b_{j}}dp_{i - 1, k} + 1\)
时间复杂度:\(O(n^{3})\)
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN = 2e3+5;
const ll INF = LONG_LONG_MAX;
ll dp[MAXN][MAXN], n, a[MAXN], b[MAXN], ans;
int main()
{
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1; i <= n; i ++)
cin >> a[i];
for(int i = 1; i <= n; i ++)
cin >> b[i];
a[0] = b[0] = -INF;
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= n; j ++)
{
if(a[i] != b[j]) dp[i][j] = dp[i - 1][j];
else
{
for(int k = 0; k < j; k ++)
{
if(b[k] < b[j]) dp[i][j] = max(dp[i - 1][k] + 1, dp[i][j]);
}
}
ans = max(ans, dp[i][j]);
}
}
cout << ans << endl;
return 0;
}
思路优化:
在转移过程中,我们把 \(0 \le k < j, b_{k} > b_{j}\) 的 \(k\) 构成的集合称为 \(dp_{i,j}\) 进行状态转移时的决策集合,记为 \(S(i,j)\) 则 \(S(i,j+1) =\begin{cases} \qquad S(i,j) ~~\quad b_{j} \ge a_{i} \\ S(i,j) \bigcup \left \{ j\right \} \quad b_{j} < a_{i} \end{cases}\)
引入决策集合使得时间复杂度降为 \(O(n^{2})\)
for(int i = 1; i <= n; i ++)
{
ll val = dp[i - 1][0];
// val是决策集合S(i,j)中dp[i-1][k]的最大值
// j = 1时,0可以作为k的取值,因此val这样初始化
for(int j = 1; j <= n; j ++)
{
if(a[i] != b[j]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = val + 1;
//j即将增大为 j + 1,检查 j 是否进入新的决策集合
if(b[j] < a[i]) val = max(val, dp[i - 1][j]);
ans = max(ans, dp[i][j]);
}
}
收获:
引入决策集合来降低时间复杂度。
对于”决策集合中的元素只增多不减少“的情形,就可以像本题一样维护一个变量来记录决策集合的当前信息,避免重复扫描,把转移的时间复杂度降低一个数量级。
例题3:POJ3666
思考前先吐槽一波:读完题感觉这是一道原题,之前好像碰到过类似的题,这也许是一道很典的题吧。当然以后遇到这样的题也为我提供了一种新的思路。
思考:
因为要构造非严格单调递增序列和非严格单调递减序列 \(B\) 很容易想到和上一题有相似之处?
对于样例:
7
1 3 2 4 5 3 9
它的最长非严格递增序列是 1 3 4 5 9
考虑 \(B\)
1 3 2 4 5 3 9
1 3 x 4 5 x 9
\(x\) 为待填值,我们先考虑求出 最长非严格递增序列的时间复杂度:\(O(n^{2})\) 当然可以用贪心思路优化成 \(O(nlog_{2}{n})\) 但是我突然意识到好像不可做?因为我只能够得到最长的严格递增序列长度是 5 并不能求出 1 3 4 5 9 这个序列。
到这里就卡住了,呜呜呜,菜菜。。。
正解:
首先证明一个引理:
在满足 \(S\) 最小化的前提下,一定存在一种构造序列 \(B\) 的方案,使得 \(B\) 中的数值都在 \(A\) 中出现过。
这个结论虽然我猜出来了,但是还是看一下大佬怎么证明的吧。

打括号的地方可以忽略。
其实证明还蛮简单的,那么引理得到证明后我们如何运用呢?
小疑问和思考:先说一个这这里发现的比较重要的一个点,书中在这里单独提了一嘴:”我们依次考虑:完成前 \(i\) 个数的构造时, \(S\) 的最小值。也就是把 DP 的 ”阶段“ 设为已经处理完的前缀序列长度。“ 这里书上再一次提到了对于 **”阶段“ **的说明,本人在一开始理解 ”阶段“ 的概念是比较迷惑的, 但是秉持着 ”存在即合理,存在就一定能够被解释,被理解“ 的观点我决定将 ”阶段“ 这个概念给弄清楚,如果有读者觉得这一段太过 制杖 繁琐,可以跳过。
先看到作者对于 ”阶段“ 的定义: 动态规划算法把原问题视作若干个重叠子问题的逐层递进,每个子问题的求解过程都构成一个 ”阶段“ 。
再看到书中对于 ”阶段“ 的划分:



相比于动态规划三要素的 ”状态“ 和 ”决策“ ,”阶段“ 确实显得更为抽象,为了进一步理解 ”阶段“ 这个概念,我在图书馆借了一本《运筹学》 ,其中对于 ”阶段“ 这一概念是这样解释的:

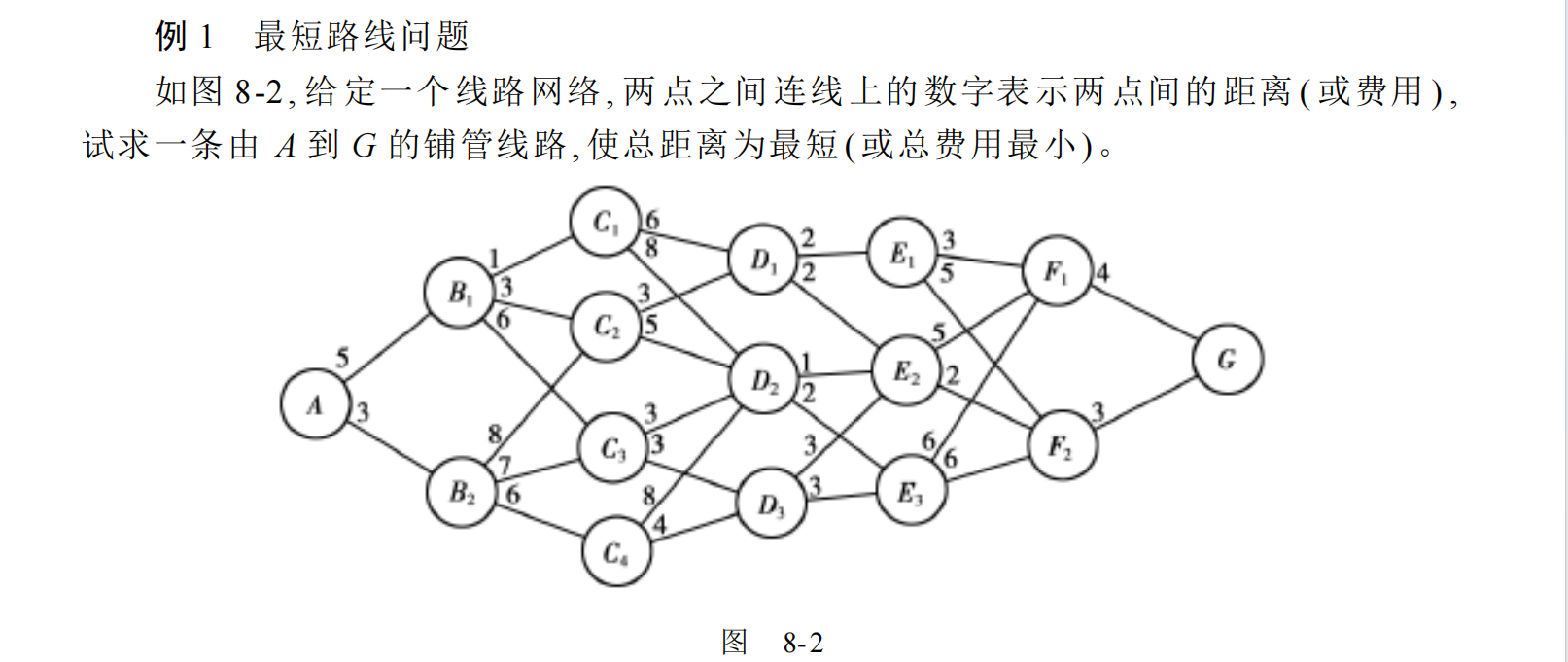
好吧,那么对于 ”阶段“ 的概念其实我也大概了解了,这里提出一个 小问题 :
书中在方法二写道:”既然仅把 DP 的 ”阶段“ 要素(即已经处理的序列长度)放在 DP 状态中不足以执行转移……“,这里有个很关键的信息就是 ”把 DP 的 ”阶段“ 要素(即已经处理的序列长度)放在 DP 状态“ 不知道是我粗心的原因还是什么,书中前文好像从来没有讲过要把 ”阶段“ 放在 DP 的 ”状态“ 里面。我的问题就是:在所有的 DP 中将 ”阶段“ 放在 DP 的 “状态” 里面是必须的吗?换句话说,是不是所有 DP 的 “状态” 都 包含它本身的 “阶段”?
方法一:
定义 \(dp_{i}\) 表示完成前 \(i\) 个数的构造,并且 \(b_{i} = a_{i}\) 时,\(S\) 的最小值。
根据 DP 含义自己推的状态转移:
\(dp_{i} = \min_{0 \le j < i, a_{j} \le a_{i}} \left \{ dp_{j} + cost(j + 1, i - 1) \right \}\)
\(cost(x, y)\) 表示 $ {\textstyle \sum_{i = x}^{y}|a_{i} - b_{i}|} $
这个状态转移方程其实很好推出,而且我们会发现计算 \(cost(x, y)\) 和我们一开始确定序列:1 3 x 4 5 x 9 中 x 的取值算的是一个东西。
计算 \(cost(x, y)\) 其实非常简单,就是另前面某部分等于 \(a_{j}\) 后面某一部分等于 \(a_{i}\) 。
时间复杂度:\(O(n^{4})\)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN = 2e5+5;
const ll INF = 1e14 + 5;
ll Tex = 1, n, a[MAXN], b[MAXN], dp[MAXN], ans;
ll fun_dp1()
{
ll res = INF;
memset(dp, 0x3f, sizeof dp);
dp[0] = 0;
for(int i = 1; i <= n; i ++)
{
for(int j = 0; j < i; j ++)
{
if(a[j] <= a[i])
{
for(int k = j; k <= i; k ++)
{
ll cost = 0;
for(int x = j; x <= k; x ++)
cost += abs(a[x] - a[j]);
for(int x = k + 1; x <= i; x ++)
cost += abs(a[x] - a[i]);
dp[i] = min(dp[i], dp[j] + cost);
}
}
}
}
for(int i = 1; i <= n; i ++)
{
ll cost = 0;
for(int j = i + 1; j <= n; j ++)
cost += abs(a[j] - a[i]);
res = min(res, dp[i] + cost);
}
return res;
}
ll fun_dp2()
{
ll res = INF;
memset(dp, 0x3f, sizeof dp);
dp[0] = 0;
for(int i = 1; i <= n; i ++)
{
for(int j = 0; j < i; j ++)
{
if(b[j] <= b[i])
{
for(int k = j; k <= i; k ++)
{
ll cost = 0;
for(int x = j; x <= k; x ++)
cost += abs(b[x] - b[j]);
for(int x = k + 1; x <= i; x ++)
cost += abs(b[x] - b[i]);
dp[i] = min(dp[i], dp[j] + cost);
}
}
}
}
for(int i = 1; i <= n; i ++)
{
ll cost = 0;
for(int j = i + 1; j <= n; j ++)
cost += abs(b[j] - b[i]);
res = min(res, dp[i] + cost);
}
return res;
}
void AC()
{
cin >> n;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
b[n - i + 1] = a[i];
}
ans = min(fun_dp1(), fun_dp2());
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(false);
// cin >> Tex;
while(Tex --) AC();
return 0;
}
**TLE ** 只过了 \(50\%\) 呜呜呜...
书上讲的时间复杂度是 \(O(n^{3})\) 但是我这里总的时间复杂度是 \(O(n^{4})\) 所以那里出问题了呢?
我们想想是不是可以预处理出所有的 \(cost(x, y)\) 值。
当然发现其实也不用预处理,我们这里求 \(cost(x, y)\) 完全可以砍掉一层 \(for\) 。
ll cost = 0;
for(int x = j + 1; x < i; x ++)
cost += abs(a[x] - a[i]);
//cost 先默认为全部都是 a[i] 时的花费
for(int k = j + 1; k < i; k ++)
{
cost -= abs(a[k] - a[i]);
cost += abs(a[k] - a[j]);
//将 a[k] 变成 a[j]
dp[i] = min(dp[i], dp[j] + cost);
}
dp[i] = min(dp[i], dp[j] + cost);
//可能第一次没进循环
再交一发, WA 了,过了 \(70\%\) 的点,难道那里写错了???
仔细看一遍,原来是最后一行,虽然可能第一次没进循环,但是也可能进了循环但是实际上全为 \(a_{i}\) 时候最优,但是这里会把值更新掉,所以把它放在前面去。
ll cost = 0;
for(int x = j + 1; x <= i; x ++)
cost += abs(b[x] - b[i]);
//cost 先默认为全部都是 a[i] 时的花费
dp[i] = min(dp[i], dp[j] + cost);
//可能第一次没进循环
for(int k = j + 1; k < i; k ++)
{
cost -= abs(b[k] - b[i]);
cost += abs(b[k] - b[j]);
//将 a[k] 变成 a[j]
dp[i] = min(dp[i], dp[j] + cost);
}
再交一发,又 TLE 了,过了 \(80\%\) 的点,OK,此时已经是方法一的极限了吗?书上在说方法一的时间复杂度是 \(O(n^3)\) 时,方法一就结束了。我们发现此时每一层 \(for\) 貌似都已经砍不了了,那么我们先看看方法二吧。
方法二:
既然仅仅把 DP 的 "阶段" 要素(即已经处理的序列长度)放在 DP 状态中不足以执行转移,一个直接的想法
就是吧 \(B\) 序列的最后一个值也记录在 \(DP\) 状态里面。
定义 \(dp_{i,j}\) 表示完成前 \(i\) 个数的构造,其中 \(B_{i} = j\) 时,\(S\) 的最小值。
思考:
之前讨论过这个 "阶段" 要素在 DP "状态" 定义中是否必要这个话题,虽然没有讨论出结果,但是凭直觉我觉得应该是必要的。那么记住这个结论,那就是:“阶段” 要素在 DP “状态” 定义中是必要的。
那么这里通过多引入一维 “状态“ 有什么用呢?
其实发现对于 “状态” 的不同定义也就是对集合不同方式的划分。
那么对于多引入一维状态实际上是将集合划分为更为细致的部分,对于原来的划分,我们只存在 "阶段" 这一 "阶段" 变量。
这里突然插一句题外话:
我发现真正理解书中所指的 ”阶段“ 这一概念究竟是什么意思了。
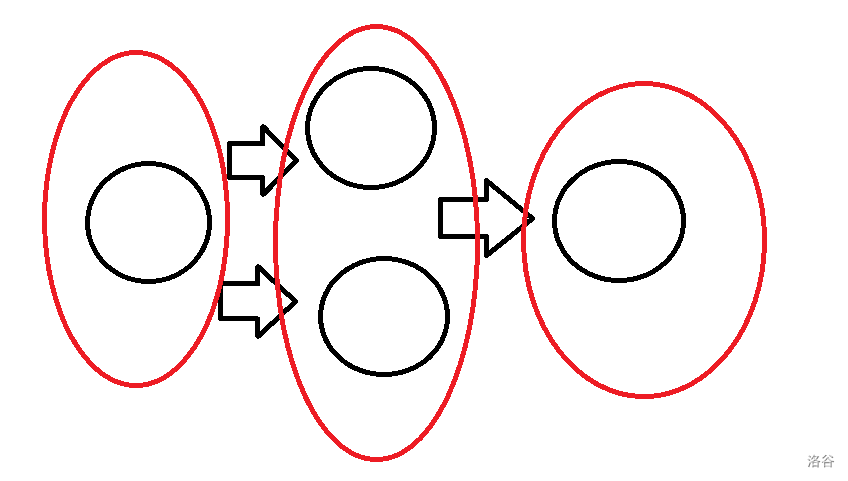
这里动态规划的三要素 "状态" "转移" "阶段" 分别对应的是 “黑色的圆圈” ”箭头“ ”红色的圆圈“。
那么阶段其实就是我们枚举的顺序,对于 "状态" 的计算 来说,状态之间的计算来源于 状态之间的 "转移",
而 ”转移“ 的先后顺序 其实就是我们的 "阶段" (这样描述可能有点不妥,但是大家能够体会就行)。
OK,那么我对 DP 的基本概念的理解更加深入了,那么我们言归正传,继续我们的思考。
思考:
上面说到:
那么对于多引入一维状态实际上是将集合划分为更为细致的部分,对于原来的划分,我们只存在 "阶段" 这一 划分。
如果我们再引入一个变量,那么我们对集合的划分更加细致,同时,我们存储的信息就更多了,我想书的作者是想通过这 存储的更多的信息 去推出我们 方法一 需要单独去求的 \(cost(x, y)\)。
说回方法二:
通过 "状态" 的定义,尝试写出状态转移方程: \(dp_{i,j} = \min_{0 \le k \le j} \left \{dp_{i - 1, k} + |a_{i} - j| \right\}\)。
当然这里要对 \(a\) 进行 离散化 处理。
那么我们根据方法二尝试写出以下代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN = 2e3+5;
const ll INF = 1e14 + 5;
ll Tex = 1, n, a[MAXN], b[MAXN], c[MAXN], dp[MAXN][MAXN], ans, len;
unordered_map<ll, ll> mp, f_mp;
ll dp1()
{
ll res = INF;
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0;
for(int i = 1; i <= n; i ++)
{
for(int j = 0; j < len; j ++)
{
for(int k = 0; k <= j; k ++)
{
dp[i][j] = min(dp[i - 1][k] + abs(f_mp[a[i]] - f_mp[j]), dp[i][j]);
}
}
}
for(int i = 0; i < len; i ++)
res = min(dp[n][i], res);
return res;
}
ll dp2()
{
ll res = INF;
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0;
for(int i = 1; i <= n; i ++)
{
for(int j = 0; j < len; j ++)
{
for(int k = 0; k <= j; k ++)
{
dp[i][j] = min(dp[i - 1][k] + abs(f_mp[c[i]] - f_mp[j]), dp[i][j]);
}
}
}
for(int i = 0; i < len; i ++)
res = min(dp[n][i], res);
return res;
}
void AC()
{
cin >> n;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
b[i] = a[i];
}
sort(b + 1, b + n + 1);
len = unique(b + 1, b + n + 1) - (b + 1);
for(int i = 1; i <= len; i ++)
{
mp[b[i]] = i - 1;
f_mp[i - 1] = b[i];
}
for(int i = 1; i <= n; i ++)
{
a[i] = mp[a[i]];
c[n - i + 1] = a[i];
}
//离散化
ans = min(dp1(), dp2());
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(false);
// cin >> Tex;
while(Tex --) AC();
return 0;
}
时间复杂度:\(O(n^{3})\),不出意外 \(TLE\) 过了 \(70\%\) 的点。
吐槽: DP 是真的难啊,思路难想,细节还多,呜呜呜......
怎么砍这一层 \(for\) 呢?想到上一道题的思路,引入决策集合 \(S(i, j)\)
怎么引入呢?我们注意到上一题是这样定义 \(S(i,j)\) 的:
我们把满足 \(0 \le k < j, b_{k} < a_{i}\) 的 \(k\) 构成的集合称为 \(dp_{i,j}\) 进行状态转移时的决策集合,记为 \(S(i,j)\)。
同样这个题我们可以定义:
我们把满足 \(0 \le k \le j\) 的 \(k\) 构成的集合称为 \(dp_{i,j}\) 进行状态转移时的决策集合,记为 \(S(i,j)\)。
\(S(i,j+1) = S(i,j) \bigcup \left \{ j\right \}\)
于是可以这样改:
for(int i = 1; i <= n; i ++)
{
ll val = dp[i - 1][0];
for(int j = 0; j <= len; j ++)
{
val = min(val, dp[i - 1][j]);
dp[i][j] = min(val + abs(f_mp[a[i]] - f_mp[j]), dp[i][j]);
}
}
最终代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN = 2e3+5;
const ll INF = 1e14 + 5;
ll Tex = 1, n, a[MAXN], b[MAXN], c[MAXN], dp[MAXN][MAXN], ans, len;
unordered_map<ll, ll> mp, f_mp;
ll dp1()
{
ll res = INF;
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0;
for(int i = 1; i <= n; i ++)
{
ll val = dp[i - 1][0];
for(int j = 0; j <= len; j ++)
{
val = min(val, dp[i - 1][j]);
dp[i][j] = min(val + abs(f_mp[a[i]] - f_mp[j]), dp[i][j]);
}
}
for(int i = 0; i <= len; i ++)
res = min(dp[n][i], res);
return res;
}
ll dp2()
{
ll res = INF;
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0;
for(int i = 1; i <= n; i ++)
{
ll val = dp[i - 1][0];
for(int j = 0; j <= len; j ++)
{
val = min(val, dp[i - 1][j]);
dp[i][j] = min(val + abs(f_mp[c[i]] - f_mp[j]), dp[i][j]);
}
}
for(int i = 0; i <= len; i ++)
res = min(dp[n][i], res);
return res;
}
void AC()
{
cin >> n;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
b[i] = a[i];
}
sort(b, b + n + 1);
len = unique(b , b + n + 1) - (b + 1);
for(int i = 0; i <= len; i ++)
{
mp[b[i]] = i;
f_mp[i] = b[i];
}
for(int i = 1; i <= n; i ++)
{
a[i] = mp[a[i]];
c[n - i + 1] = a[i];
}
//离散化
ans = min(dp1(), dp2());
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(false);
// cin >> Tex;
while(Tex --) AC();
return 0;
}
时间复杂度:\(O(n^{2})\),运行时间 \(108ms\) 完美通过!!!
终于过了呜呜呜┭┮﹏┭┮,改了三个小时。
例题4:Mobile Service
思考:
不难想到怎么去定义 DP 的状态。
经过前面三题的学习,我总结出了我定义 DP 状态的方法:
1.明确 "阶段", 在我们前面有讨论过,"阶段" 在 状态的表示中必不可少。
2.看看 “阶段” 是不是能够包含题目所需要的所有信息,如果不能够包含就定义新的变量直到能够全部包含为止。
那么这个题的 “阶段” 就是 “已经完成的请求数目”,发现 "阶段" 的信息不能够完全包含题目所需要的所有信息,我们要能够知道每个服务员的具体状态才能够完成各个 DP “阶段” 的计算,因此我们可以定义:
\(dp_{x,i,j,k}\) 表示已经处理完前 \(x\) 个请求数目,且当前当前三个服务员的位置在 \(i,j,k\) 的最小花费 并且 \(i \neq j \neq k\)。
我们最终求的最小花费就是 \(\min_{1 \le i,j,k \le n}{dp_{n,i,j,k}}\) 并且 \(i \neq j \neq k\)。
但是我们会发现这样定义是空间是爆炸,所以能不能砍点一维呢?
正解:
在第 \(i\) 个请求完成时,一定有一个员工处于 \(p_{i}\) (这里的 \(p_{i}\) 表示的是第 \(i\) 个请求的位置),那么只需要知道 "阶段" \(i\) 和另外两个员工的位置即可描述一个状态,处于 \(P_i\) 的员工位置信息对于 DP 来说是冗杂信息。
因此定义 \(dp_{x,i,j}\) 表示完成了前 \(x\) 个请求,其中一个员工位于 \(p_x\) ,另外两个员工位于 \(i,j\) 的最小花费。
这里我们用例题 \(1\) 的状态转移方法:通过当前状态看下一个状态转移到哪里去写状态转移方程。
\(dp_{x + 1, i, j} = \min \left \{ dp_{x + 1, i , j} , dp_{ x, i, j} + cost(p_x, p_{x + 1})\right \}\)。
\(dp_{x + 1, p_x, j} = \min \left \{ dp_{x + 1, p_x, j} , dp_{ x, i, j} + cost(i, p_{x + 1})\right \}\)。
\(dp_{x + 1, i, p_{x}} = \min \left \{ dp_{x + 1, i, p_{x}} , dp_{ x, i, j} + cost(j, p_{x + 1})\right \}\)。
当然还要判断转移的合法性,\(i \neq j \neq p_{x+1}\)。
时间复杂度 \(O(NL^2)\) 。
OK,以下是 AC 代码:
#include<bits/stdc++.h>
using namespace std;
typedef int ll;
const ll MAXN = 1005;
const ll MAXL = 205;
const ll INF = 1e9;
ll Tex = 1, N, L, p[MAXN], mp[MAXL][MAXL], dp[MAXN][MAXL][MAXL], ans;
ll cost(ll x, ll y)
{
return mp[x][y];
}
void AC()
{
cin >> L >> N;
memset(p, 0, sizeof p); ans = INF;
for(int i = 1; i <= L; i ++)
for(int j = 1; j <= L; j ++)
cin >> mp[i][j];
for(int i = 1; i <= N; i ++)
cin >> p[i];
memset(dp, 0x3f, sizeof dp);
dp[0][1][2] = 0; p[0] = 3;
for(int x = 0; x <= N; x ++)
{
for(int i = 1; i <= L; i ++)
{
for(int j = 1; j <= L; j ++)
{
if(i == p[x] || j == p[x] || i == j) continue;
dp[x + 1][i][j] = min(dp[x + 1][i][j], dp[x][i][j] + cost(p[x], p[x + 1]));
dp[x + 1][p[x]][j] = min(dp[x + 1][p[x]][j], dp[x][i][j] + cost(i, p[x + 1]));
dp[x + 1][i][p[x]] = min(dp[x + 1][i][p[x]], dp[x][i][j] + cost(j, p[x + 1]));
}
}
}
for(int i = 1; i <= L; i ++)
for(int j = 1; j <= L; j ++)
ans = min(dp[N][i][j], ans);
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(false);
// cin >> Tex;
while(Tex --) AC();
return 0;
}
做到这里感觉这个例题比前面简单不少。
收获:
说实话有点惊讶,因为发现书中最后对这个题的小结有我对这个题思考时候的阐述。
1.求解线性 DP 问题,一般确定 ”阶段“,若 "阶段" 不足以表示一个状态,则可以把所需的附加信息也作为状态的维度。
2.在确定 DP 状态时,要选择最小的能够覆盖整个状态空间的 "维度集合"。
例题5:传纸条
分析:
首先注意到此题的数据范围比较小,那么 DP 维数可以定义很大。
我们首先找到 ”阶段“ 是什么呢?
就直接以时间为 ”阶段“ 好了。因为他们每时每刻同时移动。
在分析缺少什么呢?
没错,就是两个人的位置信息。
那么定义 \(dp_{t,idx_1,idy_0,idx_2,idy_2}\) 为已经移动 \(t\) 秒两人最后分别移动到 \((idx_1,idy_1)\) 和 \((idx_2,idy_2)\) 时的好心程度之和的最大值。
不难写出状态转移方程:
\(dp_{t,idx_1+1,idy_1,idx_2+1,idy_2} = \min \left \{ dp_{t,idx_1+1,idy_1,idx_2+1,idy_2} , dp_{t,idx_1,idy_0,idx_2,idy_2} + cost\right \}\)。
\(dp_{t,idx_1+1,idy_1,idx_2,idy_2+1} = \min \left \{ dp_{t,idx_1+1,idy_1,idx_2,idy_2+1} , dp_{t,idx_1,idy_0,idx_2,idy_2} + cost\right \}\)。
\(dp_{t,idx_1,idy_1+1,idx_2+1,idy_2} = \min \left \{ dp_{t,idx_1,idy_1+1,idx_2+1,idy_2} , dp_{t,idx_1,idy_0,idx_2,idy_2} + cost\right \}\)。
\(dp_{t,idx_1,idy_1+1,idx_2,idy_2+1} = \min \left \{ dp_{t,idx_1,idy_1+1,idx_2,idy_2+1} , dp_{t,idx_1,idy_0,idx_2,idy_2} + cost\right \}\)。
当然还有很多约束条件。
正解:
和我思路差不多,但是有很多优化,因为 \(50\times50\times50\times50\times50\) 的空间是爆炸的,当时没有注意到。
虽然注意到数据范围比较小,但是空间限制也比较小。
这里,书上的阶段与我定义的阶段略有出入,那就是定义路径长度,我们会发现,路径总长度每次会增加 \(1\)。
不难推出以下关系
\(idx_1 + idy_1 = idx_2 + idy_2 = i + 2\)。
那么可以只定义三个维度。
\(dp_{i,idx_1,idx_2}\) 表示两个路径的长度均为 \(i\) ,第一条路径的结尾的横坐标为 \(idx1\),第二条路径的结尾横坐标为 \(idx_2\) 时,已经取得数之和的最大值。
不难写出代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN = 55;
ll Tex = 1, n, m, mp[MAXN][MAXN], dp[MAXN << 1][MAXN][MAXN];
int dx1[4] = {1, 1, 0, 0};
int dx2[4] = {1, 0, 1, 0};
void AC()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
cin >> mp[i][j];
memset(dp, -0x3f, sizeof dp);
dp[2][1][1] = mp[1][1];
for(int i = 2; i <= n + m; i ++)
{
for(int idx1 = 1; idx1 <= n; idx1 ++)
{
for(int idx2 = 1; idx2 <= n; idx2 ++)
{
for(int k = 0; k < 4; k ++)
{
int xx1 = idx1 + dx1[k];
int xx2 = idx2 + dx2[k];
int yy1 = (i + 1) - xx1;
int yy2 = (i + 1) - xx2;
if(xx1 > n || xx2 > n || yy1 > m || yy2 > m) continue;
if(xx1 == xx2) dp[i + 1][xx1][xx2] = max(dp[i + 1][xx1][xx2], dp[i][idx1][idx2] + mp[xx1][yy1]);
else dp[i + 1][xx1][xx2] = max(dp[i + 1][xx1][xx2], dp[i][idx1][idx2] + mp[xx1][yy1] + mp[xx2][yy2]);
}
}
}
}
cout << dp[n + m][n][n] << endl;
}
int main()
{
ios::sync_with_stdio(false);
// cin >> Tex;
while(Tex --) AC();
return 0;
}
时间复杂度 \(O((n+m)\times n^2)\)
例题6: I-country
先挖个坑,以后有机会再补。
例题7:Cookies
分析:
这感觉是一道不同寻常的题,因为这个问题看起来是充满后效性的,因为当前孩子分的饼干如果比之前某个孩子多,那怒气值还会上升,但是好像并不影响我们状态转移,只需要把会发怒的人数记录下来就可以了?
先大胆思考一下 \(dp_{i,j,k}\) 表示已经分完 \(i\) 个孩子,还有 \(j\) 个饼干, 第 \(i\) 个孩子分了 \(i\) 个的最小怒气值。
状态转移方程怎么写?
写出来非常麻烦就对了。
那么大概率把题做偏了。
正解:
还要先考虑贪心一下,怨气值大的得到的饼干也得要多一点,所以先按怒气值从大到小排个序那么在这个条件下是不是就可以很好的做出这个题了呢?
考虑 \(dp_{i,j}\) 表示已经分完了 \(i\) 个孩子,还有 \(j\) 个饼干的最小怒气值之和。
那么状态转移方程怎么写呢?
其实直接写出来也不容易,得换一种思路去转移。
等价转化一下,
1.如果第 \(i\) 个孩子获得的饼干数大于 \(1\) ,则等价于分配 \(j -i\) 个饼干给前 \(i\) 个孩子,获得饼干的相对大小顺序不变,从而怨气之和也不变。
2.如果第 \(i\) 个孩子获得的饼干数为 \(1\) ,那么枚举前面有多少个孩子也获得 \(1\) 块饼干。
吐槽:
确实有亿点抽象,但是最后还是啃懂了。
状态转移方程:
\(dp_{i,j} = min\begin{Bmatrix}dp_{i,j-i}\\dp_{k,j-(i - k)} + k \times\sum_{p=k+1}^{i}g_{p}\end{Bmatrix}\)
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN = 35;
const ll MAXM = 5e3 + 5;
const ll INF = 1e14;
ll n, m, dp[MAXN][MAXM], ans[MAXN];
struct node{
ll id, g;
}a[MAXN];
bool cmp(node xx, node yy)
{
return xx.g > yy.g;
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m;
for(int i = 1; i <= n; i ++)
{
a[i].id = i;
cin >> a[i].g;
}
sort(a + 1, a + n + 1, cmp);
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0;
for(int i = 1; i <= n; i ++)
{
for(int j = 0; j <= m; j ++)
{
if(i <= j)
{
dp[i][j] = dp[i][j - i];
ll val = INF, sum = 0;
for(int p = 1; p <= i; p ++)
sum += a[p].g;
for(int k = 0; k < i; k ++)
{
sum -= a[k].g;
val = min(val, dp[k][j - (i - k)] + k * sum);
}
dp[i][j] = min(dp[i][j], val);
}
}
}
cout << dp[n][m] << endl;
int i = n, j = m, h = 0;
while(i)
{
if(dp[i][j] == dp[i][j - i]) j = j - i, h ++;
else
{
ll sum = 0, val;
for(int p = 1; p <= i; p ++)
sum += a[p].g;
for(int k = 0; k < i; k ++)
{
sum -= a[k].g;
val = dp[k][j - (i - k)] + k * sum;
if(dp[i][j] == val)
{
for(int p = k + 1; p <= i; p ++)
ans[a[p].id] = h + 1;
j = j - (i - k);
i = k;
break;
}
}
}
}
for(int i = 1; i <= n; i ++)
cout << ans[i] << " ";
cout << endl;
return 0;
}
收获:
有时可以通过额外的算法确定 DP 状态的计算顺序,有时可以在状态空间中运用等效手法对状态进行缩放。
在本题中,我们就用到了贪心的策略,在 DP 前对 N 个孩子执行排序,使他们获得的饼干数单调递减。我们还利用相对大小不变性,把第 \(i+1\) 个孩子获得的饼干数先缩放到 \(1\),再考虑 \(i\) 前面有几个孩子获得饼干数量相等,使需要计算的问题得到了极大的简化,容易进行维护、转移。
线性DP到此结束...(终于结束了)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号