平淡无奇的数论笔记

目录

• • 前言
  • 取整问题
  • （拓展）欧几里得
  • 逆元
  • • 拓展欧几里得法
    • 线性逆元
  • （拓展）中国剩余定理
  • 关于GCD
  • （拓展）欧拉定理
  • 欧拉函数
  • • 计算
    • $\phi (n)->\phi (nm)$
    • • m为质数
      • n,m互质
      • 其他情况
  • 组合数学
  • • 算术基本定理（唯一分解定理）
    • 所有质因数序列排列组合
  • 几何分布
  • • 不相交路径

前言

有时候会把最基本的定义忘掉……
当且仅当存在一个正整数c使得a × c = b，则正整数a是正整数b的因子。

C99规定，对非负整数取模的结果为非负整数，否则为负整数。
贝祖定理

取整问题

double->int:

$x\le yx<\lfloor y\rfloor +1$
$x>yx\ge \lfloor y\rfloor +1$
$ac\le b⟺a\le \lfloor \frac{b}{c}\rfloor$
$ac\ge b⟺a\ge \lceil \frac{b}{c}\rceil$
$ac<b⟺a<\lceil \frac{b}{c}\rceil$
$ac>b⟺a>\lfloor \frac{b}{c}\rfloor$
$ifa\le x<blen(x)=\lfloor b\rfloor -\lfloor a\rfloor$

上整->下整

$\lceil \frac{y}{x}\rceil =\lfloor \frac{y-1}{x}\rfloor +1orceil(\frac{y}{x})=\frac{y-1}{x}+1$

左零右开区间奇偶数个数

$$\begin{gathered} if0\le x<b \\ count(x,奇数)=\lfloor \frac{b}{2}\rfloor orx>>1 \\ count(x,偶数)=\lfloor \frac{b+1}{2}\rfloor orx+1>>1 \end{gathered}$$

（写公式真累）

（拓展）欧几里得

$(a,b)=d(d|a,d|b)$
$b|a$，则$(a,b)=b\times 1+a\times 0$
否则令$a=b\times d+r(r!=0)$
$r=a-b\times d$
$(a,b)|a,(a,b)|b$
$(a,b)|r$
欧几里得：$(a,b)=(b,r)$
令$d=\lfloor a/b\rfloor ,r=a\%b$
$(a,b)=(b,a\%b)$
$b|a$，则$(a,b)=b\times 1+a\times 0$
$a\%b=a-b\times \lfloor a/b\rfloor$
拓展欧几里得：$(a,b)=(a-\lfloor a/b\rfloor \times b)\times 1+b\times 0$
（不太严谨）

逆元

拓展欧几里得法

ax≡1（mod b）（ax+by=1）

$a\times x+b\times y=1$
存在逆元的条件：$(a,b)|1⟺(a,b)=1$

线性逆元

$1^{-1}\equiv 1(modp)$(p为质数)
$p=d\times i+r（d=\lfloor \frac{p}{i}\rfloor ,r=p\%i）$
$p\equiv 0(modp)$
$d\times i+r\equiv 0(modp)$
$d\times r^{-1}+i^{-1}\equiv 0(modp)$（两边乘$r^{-1}{i}^{-1}$）
$i^{-1}\equiv -d\times r^{-1}(modp)$
$i^{-1}\equiv -\lfloor \frac{p}{i}\rfloor \times (p\%i{)}^{-1}(modp)$
（注意最小正整数$(inv\%p+p)\%p$）

（拓展）中国剩余定理

$x\equiv a_1(mod{m}_1)$
$x\equiv a_2(mod{m}_2)$
$x\equiv a_k(mod{m}_k)$
$x=a_1+k_1\times m_1=a_2+k_2\times m_2$
$k_1\times m_1-k_2\times m_2=a_2-a_1$
当仅当$(m_1,m_2)|a_2-a_1$
$k_1=k_0+m_2/(m_1,m_2)\times k$
$x=a_1+(k_0\times m_1+m_2\times m_1/(m_1,m_2)\times k)$
$=(a_1-k_0\times m_1)-[m_1,m_2]\times k(k_0=x0(a_2-a_1)/(m_1,m_2)，即k_1的一个解)$
$=x_0-[m_1,m_2]\times k(x_0由k_1计算)$
（方程数减1）
.
中国剩余定理（模互质）：$x\equiv {\sum }_{i=1}^k{M}_i^{\prime }{M}_i{a}_i(modM)$
$M=m_1{m}_2{m}_k,M_i=M/m_i,M_i^{\prime }{M}_i\equiv 1(mod{m}_i)$（按方程定义模拟即可理解）

关于GCD

1. GCD递推式：GCD(a,b)=GCD(a,a%b)

2. GCD(a,a-b)=GCD(a,b)

证：GCD(a,b-a)=GCD(a,(b-a)%a)=GCD(a,(b-a+a)%a)=GCD(a,b%a)=GCD(a,b)
应用：CF1110C Meaningless Operations

（拓展）欧拉定理

如果$(a,m)=1$，那么$a^{\phi (m)}\equiv 1(modb)$
$a^c\equiv a^{c\%\phi (m)+\phi (m)}(modm),ifc\ge \phi (m)$

欧拉函数

计算

$\phi (n)=(p_1-1)p_1^{a_1-1}\times (p_2-1)p_2^{a_2-1}\times (p_k-1)p_k^{a_k-1}$

$\phi (n)->\phi (nm)$

m为质数

$n\mid m时,\phi (nm)=\phi (n)\times m$
$n\nmid m时,\phi (nm)=\phi (n)\times (m-1)$

n,m互质

$\phi (nm)=\phi (n)\times \phi (m)$

其他情况

分解因子（大概）

组合数学

$r$次上升幂：$n\times (n+1)\times (n+r-1)$
$r$次下降幂：$n\times (n-1)\times (n-r+1)$
$C_n^m=\frac{n的m次下降幂}{m!}=\frac{n!}{(n-r)!m!}$
$C_n^m=C_{n-1}^{m-1}+C_{n-1}^m$
$C_n^m=\frac{n}{m}{C}_{n-1}^{m-1}$
$C_n^m=\frac{n-m+1}{m}{C}_n^{m-1}$

算术基本定理（唯一分解定理）

唯一分解形式正因数个数为$(a_1+1)(a_2+1)(a_n+1)$
$p_i$的取法有$0$~$a_i$（$a_i+1$种）
全体正因数之和为

所有质因数序列排列组合

例题
$设x=p_0^{a_0}{p}_1^{a_1}{p}_2^{a_2}\cdots p_n^{a_n}$
$排列组合=\frac{({\sum }_{j=0}^n{a}_j)!}{{\prod }_{i=0}^n(a_i!)}$

几何分布

记每次试验中事件A发生的概率为p，试验进行到事件A出现时停止，此时所进行的试验次数为X，其分布列为：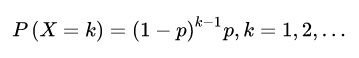
譬如，某产品的不合格率为0.05，则首次查到不合格品的检查次数X ～ GE(0.05) 。
（1）为得到1次成功而进行n次伯努利试验，n的概率分布，取值范围为1，2，3，…；
这种情况的期望和方差如下：


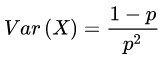
（2）m = n-1次失败，第n次成功，m的概率分布，取值范围为0，1，2，3，…。
这种情况的期望和方差如下：


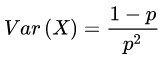
比如，假设不停地掷骰子，直到得到1。投掷次数是随机分布的，取值范围是无穷集合{ 1, 2, 3, … }，并且是一个p= 1/6的几何分布。

不相交路径

设$(a,b)$为$a$到$b$的路径条数
则$(a_1或a_2或a_n,b_1或b_2或b_n)$的不相交路径条数为
$$\left|\begin{array}{ccc}{a}_1\times b_1& a_1\times b_2& a_1\times b_n\\ a_2\times b_1& a_2\times b_2& a_2\times b_n\\ a_n\times b_1& a_n\times b_2& a_n\times b_n\end{array}\right|$$