OO第一单元总结
前言
在对这一单元的作业进行总结和分析之前,我不得我不提一句回看过去这近一个月里学OO的感受:悔恨与焦虑。悔恨是因为在假期里没有认真地学完pre的教程,一开始就拉下了基础的知识,焦虑则是在纯小白的一无所知的状态下和OO作业单打独斗(痛苦面具)。学习方法以及学习观念上存在的问题都值得我去反思,前车之覆,后车之鉴!在这过程中我着实也收获了许多,但也有很多教训和没有实现的想法,现将其整理记录下来,作为之后的警示牌或指明灯。
核心框架
第一单元作业的主要内容是在不同的限制条件下对表达式括号的展开,在去掉括号后得到正确的表达式同时进行必要的化简以减少输出字符串的长度。在第一次作业的时候,考虑到之后可能会有的迭代,我采用了指导书上递归下降的方法。但是由于之前对此一窍不通,便花了很久的时间来理解这种方法的思想和具体代码结构。
BNF描述
BNF是一种形式化符号来描述给定语言的语法一种形式化的语法表示方法。它不仅能严格地表示语法规则,而且所描述的语法是与上下文无关的。对于本单元的而言,在删去多余的空格之后,总的BNF描述如下:
表达式→[加减]项|表达式加减项
项→[加减]因子|项'∗'因子
因子→变量因子|常数因子|表达式因子
变量因子→幂函数|三角函数
常数因子→带符号的整数
表达式因子→'('表达式')'[指数]|自定义函数调用|求和函数
幂函数→(函数自变量|'i')[指数]
三角函数→'sin''('因子')'[指数]|'cos''('因子')'[指数]
自定义函数调用→自定义函数名'('因子[','因子[','因子]]')'
自定义函数名→'f'|'g'|'h'
求和函数→'sum''(''i'','常数因子','常数因子','表达式')'
指数→'∗∗'['+']允许前导零的整数
带符号的整数→[加减]允许前导零的整数
允许前导零的整数→(0|1|2|…|9)0|1|2|…|9
加减→'+'|'−'
递归下降
递归下降分析法是一种自顶而下的分析方法,文法的每个非终结符对应一个递归过程(函数)。分析过程就是从文法开始符出发执行一组递归过程(函数),这样向下推导直到推出句子;或者说从根节点出发,自顶向下为输入串寻找一个最左匹配序列,建立一棵语法树。本单元对应的文法大致如下:
Expr→Term|Expr±Term
Term→Factor|Term×Factor
Factor→Const|Pow|Expr
基于以上文法,在进行表达式时的基本框架就如下所示:
parseExpr()
parseTerm()
token = tokens[i++]
while(token == +)
parseTerm()
token = tokens[i++]
parseTerm()
parseFactor()
token = tokens[i++]
while(token == *)
parseFactor()
token = tokens[i++]
parseFactor()
架构设计
由于在第一次作业就采用了递归下降的算法,在之后的更迭中并没有很大程度的改变,所以三次作业的结构是很相似的,并没有在之后进行重构。
总体的处理流程如下:
读入→预处理→解析表达式→括号展开→优化→输出
在此流程之上,通过将各个流程以问题的形式进行分解,我逐步得到了我的代码结构。后两次作业的代码结构如下:
|- MainClass:主类
|- Parser: 表达式解析器
|- Poly: 多项式处理类
|- expr (package):表达式分解类
|- Expr: 表达式类
|- Term: 项类
|- Factor: 因子类
|- CustomFunc: 自定义函数类
|- SumFunc: 求和函数类
|- Var: 基本储存单元类
预处理
该部分主要是通过删除多余的空格、运算符来规范输入的表达式。
解析表达式
该部分即采用上述递归下降的方法解析表达式。这里会涉及两个问题,即:数据储存和自定义函数以及求和函数的解析。
数据储存
-
第一次作业的数据储存
第一次作业由于没有引入三角函数,在储存方面较为简单,我在这里将最基本的因子统一为coef*x**index的形式,在储存因子的时候采用HashMap<
BigInteger,integer>的形式,同时在每个表达式里会有Term的ArrayList,每个Term里有因子的HashMap -
第二次作业的数据储存
第二次作业由于加入了三角函数,我便把最基本的因子统一为coefx**index储存三角函数信息的
HashMap<String, Integer>,同时在每个表达式里会有Term的ArrayList,每个Term里有因子的ArrayList,而每个非表达式因子都有储存三角函数信息的HashMap<String, Integer>
自定义函数以及求和函数的解析
从上述BNF描述可知,这里将自定义函数以及求和函数都当做表达式因子,当解析到因子层面的时候,如果判断是自定义函数则交给CustomFunc类处理后,如果是求和函数则交给SumFunc类处理,处理之后将其转换为一个等价的表达式,递归解析直至因子中不在出现表达式因子
多项式处理
这部分包括括号的展开和优化
括号的展开
括号的展开的基本顺序为:
- 计算每个因子(表达式因子)的等价展开最简形式,这里通过递归调用得到
- 计算每个项的等价展开最简形式,这里通过计算这个项的所有因子相乘得到
- 计算每个表达式的等价展开最简形式,这里通过计算这个表达式的所有因子相加减得到
其中2、3中关于多项式的相乘、相加通过polynomial.polyMult、polynomial.polyAdd实现,而表达式、项和因子中都有一个Var的ArrayList由来储存展开后的结果
优化
优化部分也是对多项式的操作,该部分同样是在polynomial类中实现,包括合并同类项以及三角函数的简单化简,而在对三角函数的优化时我仅仅化简了三角函数平方和,通过对最终结果中因子中的储存三角函数信息的HashMap<String, Integer>进行二重遍历,找到满足合并条件的两个项进行合并,直到不存在能合并的两个项为止
虽然三次作业整体代码框架没有大的改变,但是由于是首次以面向对象的方式去编程,对这一思想的了解很是浅薄,以及之后因为懒惰并没有进行大范围的改动而是只对第一次的框架进行缝缝补补,整个代码结构似乎显得面向过程与面向对象两不像
度量分析
利用代码度量,开发人员可以了解哪些类型或方法应该完善或进行更彻底的测试,也可以识别出潜在的风险、了解项目的状态。而这里复杂度的分析由idea的插件MetricsReload生成,生成之后进行了分析。该插件中的各个指标的内涵如下:
类复杂度指标:
OCavg代表类的方法的平均循环复杂度
OCmax代表类的方法的最大循环复杂度
WMC代表类的总循环复杂度。
方法复杂度指标:
ev(G)基本复杂度,衡量程序非结构化程度,基本复杂度高意味着非结构化程度高,难以模块化和维护。
iv(G)模块设计复杂度,衡量模块判定结构,即模块和其他模块的调用关系;模块设计复杂度高意味模块耦合度高,这将导致模块难于隔离、维护和复用。
v(G)圈复杂度,衡量一个模块判定结构的复杂程度,根据程序从开始到结束的线性独立路径数量计算得到,圈复杂度越高,代码越复杂越难维护。
hw1
UML图与类结构
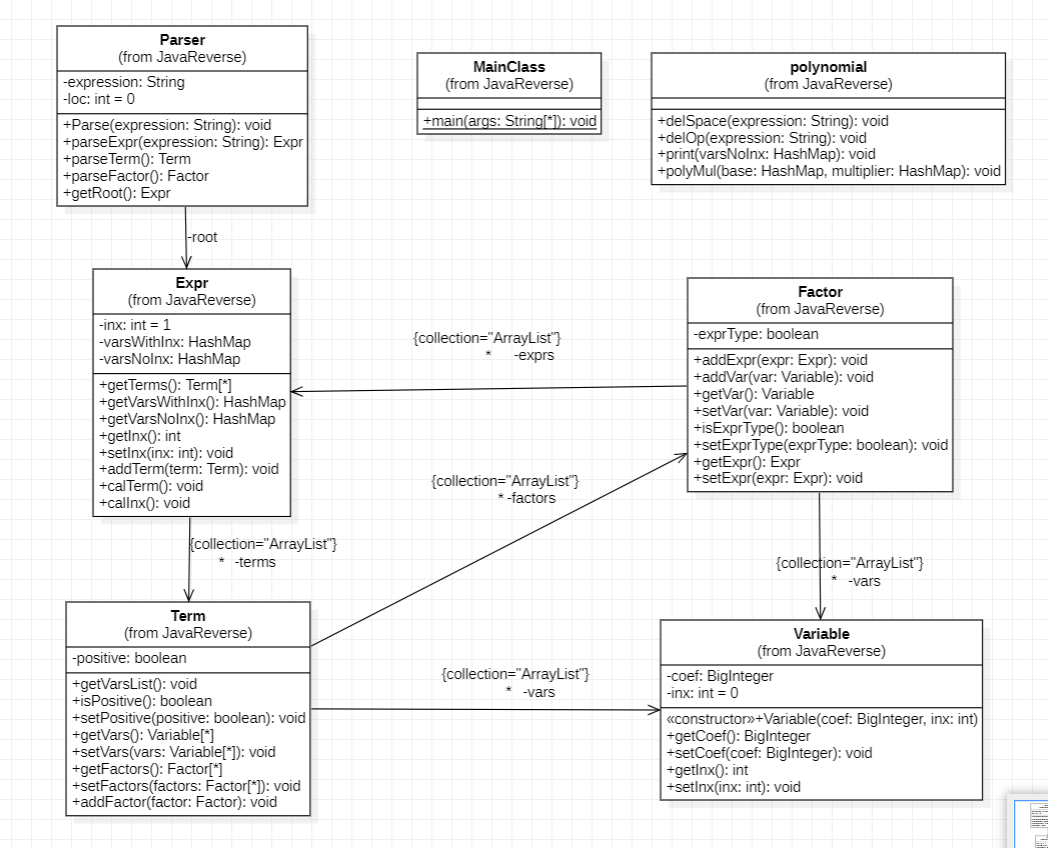
在第一次作业中,我并没有尝试实用接口,而是给Factor类添加了一个因子类型的属性以及各个类型的存储空间,这是的整体结构的调用包含关系比较混乱,也就容易出现各种类与类之间数据处理之间的复杂程度。
类复杂度分析
类复杂度分析图如下:
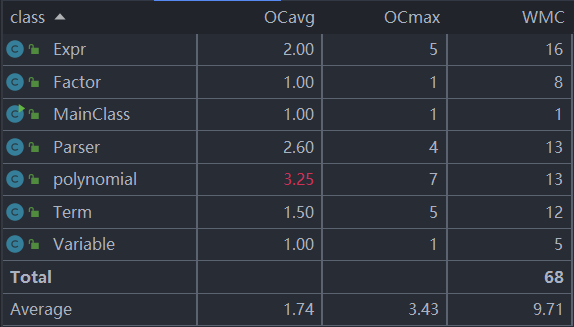
在类分析中,很明显地发现polynomial类,Parser类的各项复杂度明显很高,在扩展性和维护性上明显不足。Parser类中涉及到了分解字符串以及构建表达式树的任务,导致平均操作复杂度较高;而polynomial类中主要有因子相乘的计算、合并同类项以及最终的输出,平均操作复杂度较高。
方法复杂度分析
方法复杂度分析图如下:
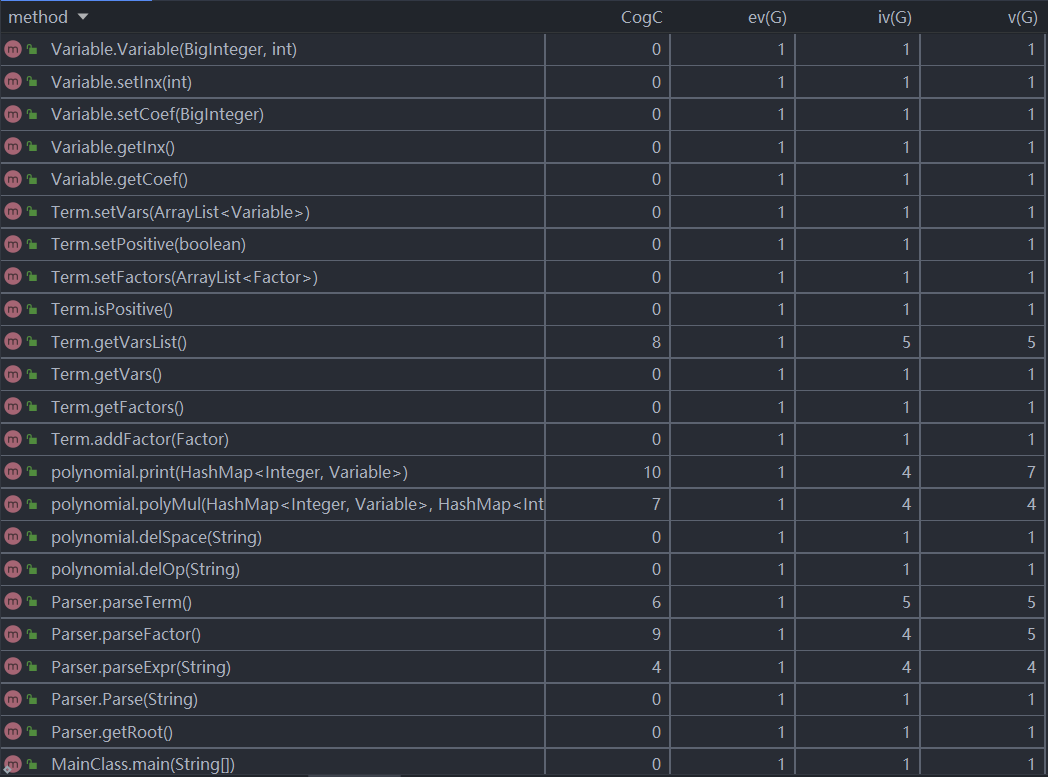
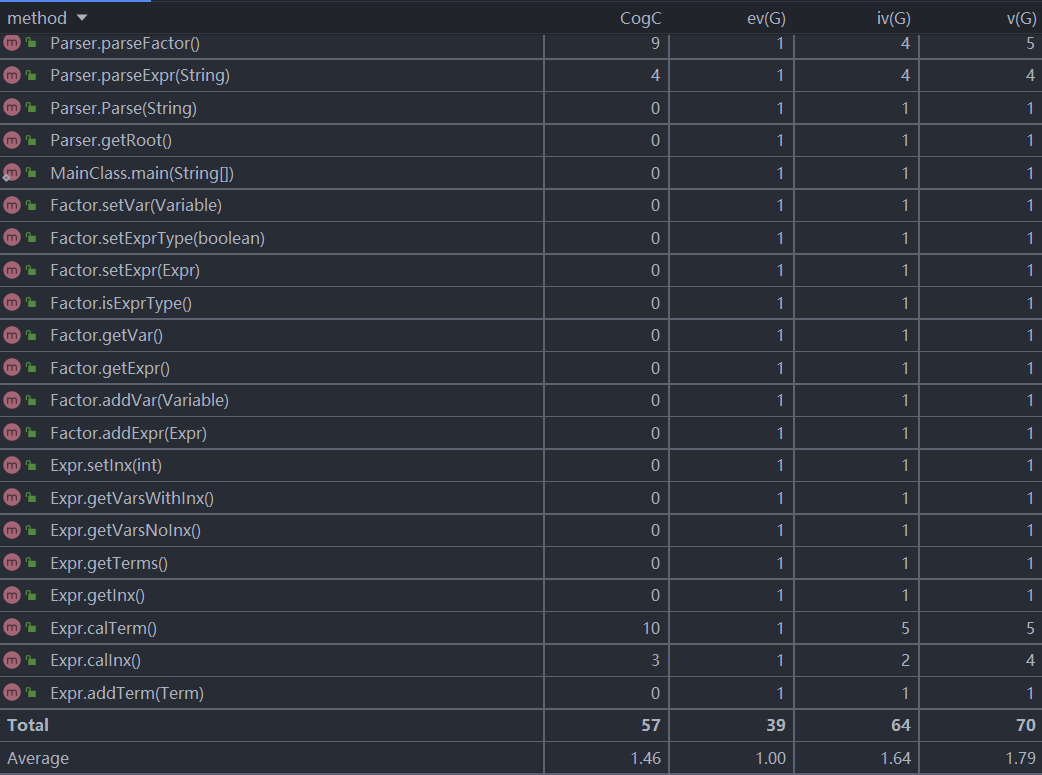
从方法的复杂度度量可以看到calTerm、print、polyMul等方法的模块设计复杂度和圈复杂度都很高。总的来说,第一次作业比较面向过程编程,主要操作方法过于集中,导致复杂度较高。其中print主要是判断路径过多。由于没有改写toString方法而是通过这一方法来输出,判断的路径过多,而且复用代码量大。
hw2 & hw3
UML图与类结构
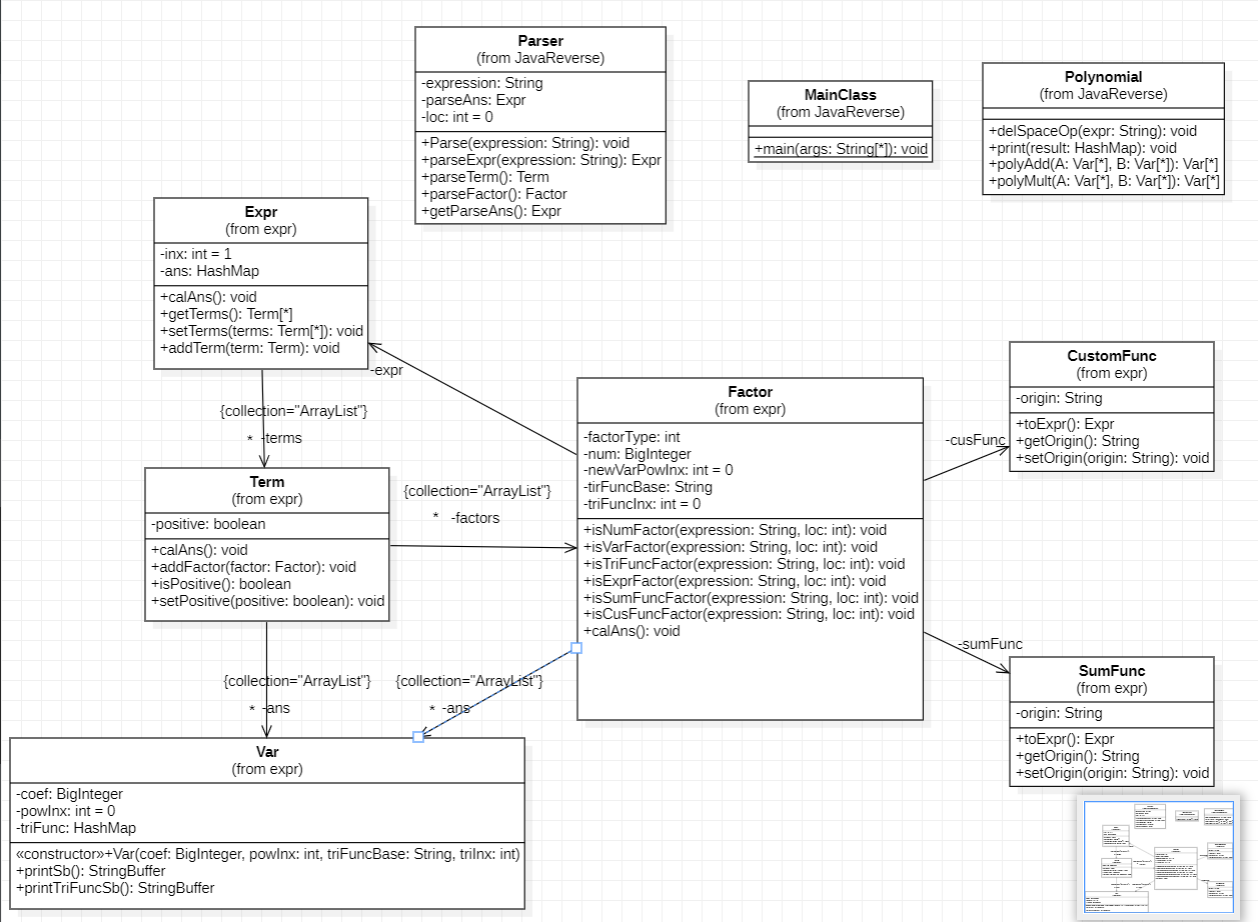
在第二次以及之后的作业中,我同样没有使用接口以及继承,而是沿用第一次作业的整体框架,给Factor类添加了一个因子类型的属性以及各个类型的存储空间,并在这个类中实现对各种类型因子的调用和构建,这无疑使得其复杂度很高,很自然地就出现了很多bug。
类复杂度分析
类复杂度分析图如下:
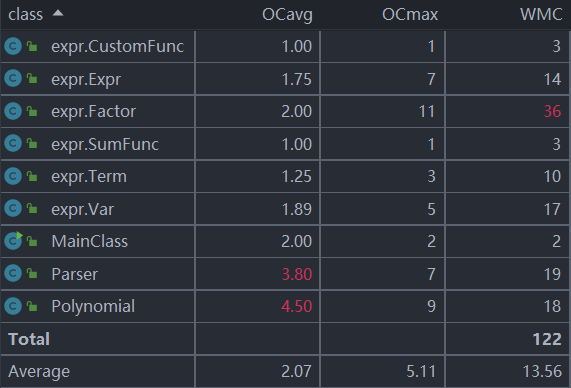
在类分析中,很明显地发现同样是polynomial类,Parser类的各项复杂度明显很高,在扩展性和维护性上明显不足,这是由于之后的作业并依旧是按照第一次的思路和框架来展开。而在第二次和第三次作业中,由于增加了三角函数、自定义函数等,Parser类中同样涉及到了分解字符串以及构建表达式树的任务,导致平均操作复杂度较高;而polynomial类中主要有因子相乘的计算、合并同类项以及最终的输出,平均操作复杂度较高。
方法复杂度分析
方法复杂度分析图如下(截取了复杂度较高的一部分):
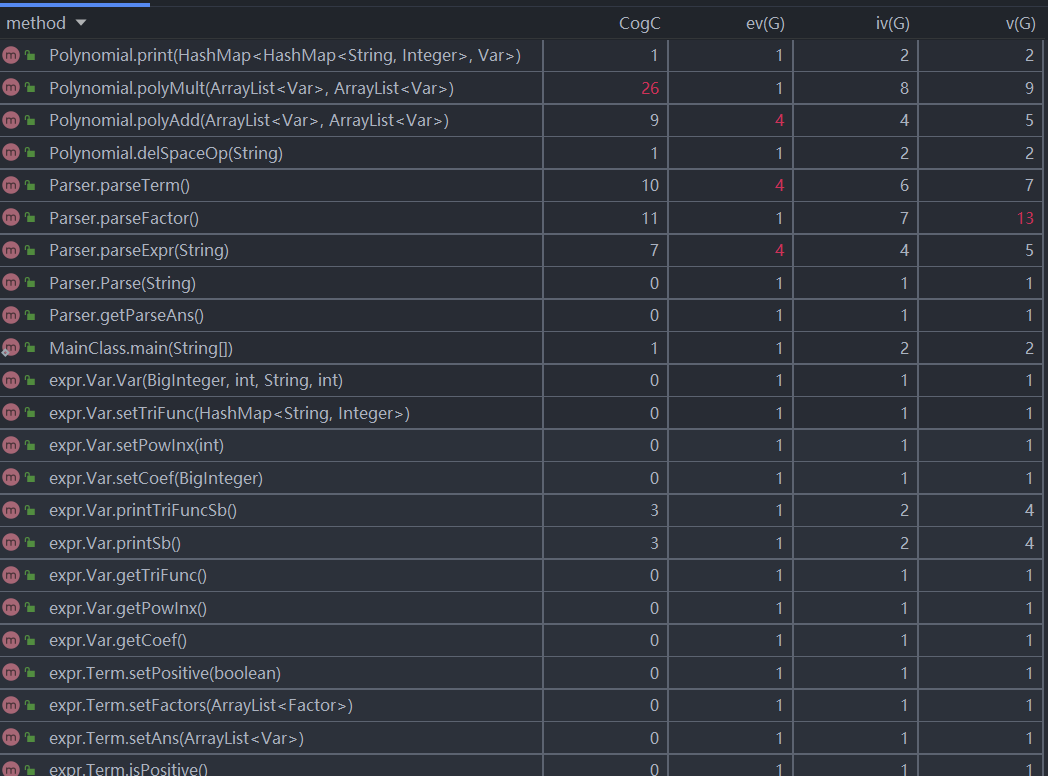
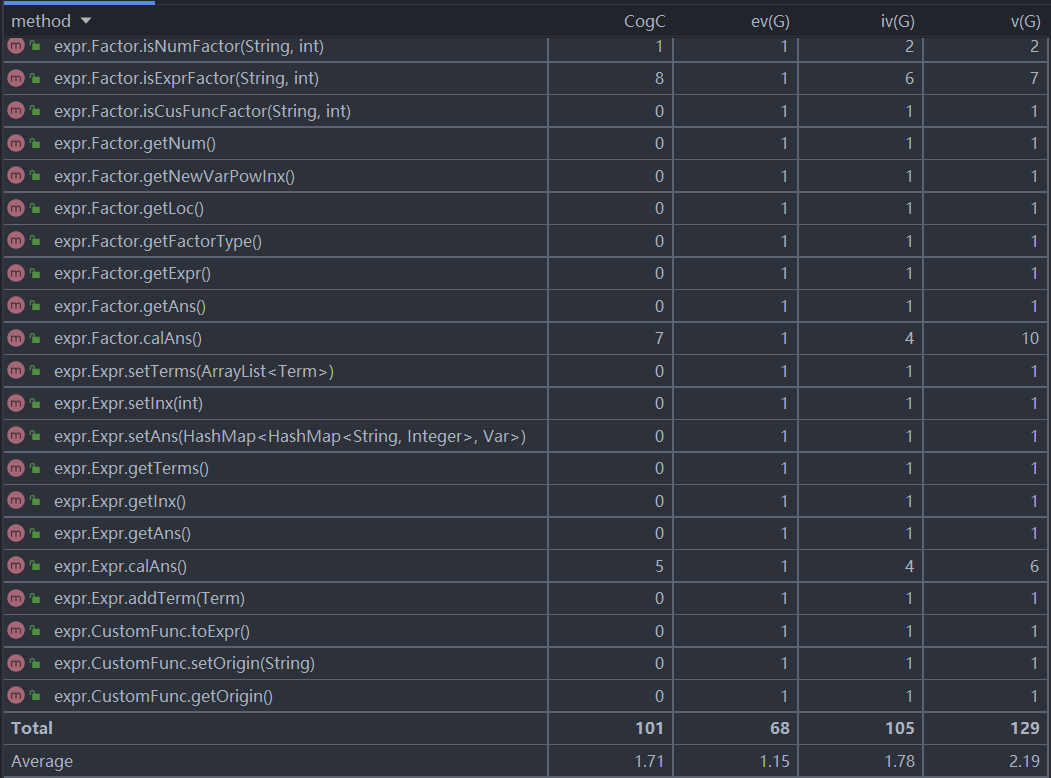
从方法的复杂度度量可以看到所有的解析方法各项复杂度都很高。这是由于括号嵌套引起的递归调用以及自定义函数等的存在,使得其复杂度相比第一次都有所上升;在解析的而parseFactor由于有很多判断路径使得其圈复杂度很高。同样的多项式处理中的polyMul和polyAdd由于涉及到深拷贝和多重循环以及条件语句的重复使用使得其复杂度很高。这就导致这两个方法很容易出现bug。
BUG分析
在第一次作业的时候由于对递归下降的方法不那么理解就直接去写了代码,之后发现的代码的bug真的是超级多,像是各种各样的符号问题、数据范围问题、输出时候的0、1问题,改来改去把原本就不怎么清晰的思路改的无比混乱,然而最为致命的是在第一次作业的时候遇到了深拷贝和浅拷贝的问题,看着我的代码不按着我写的思路来执行我是百思不得其解,浪费了大量的时间。这里对深拷贝和浅拷贝做一个总结如下:
- 浅拷贝:被复制对象的所有变量都含有与原来的对象相同的值,而所有的对其他对象的引用仍然指向原来的对象。即对象的浅拷贝会对“主”对象进行拷贝,但不会复制主对象里面的对象。”里面的对象“会在原来的对象和它的副本之间共享
- 深拷贝:深拷贝是一个整个独立的对象拷贝,深拷贝会拷贝所有的属性,并拷贝属性指向的动态分配的内存。当对象和它所引用的对象一起拷贝时即发生深拷贝。深拷贝相比于浅拷贝速度较慢并且花销较大
简单来说可以概括为:
深拷贝:引用对象的值等信息,复制一份一样的
浅拷贝:只复制引用,另一处修改,你当下的对象也会修改
而在第二次以及第三次作业中,同样也出现了符号问题、数据范围问题,而且由于第一次作业中的bug没有及时发现和更改,使得之后的作业bug层出不穷!在此我真切地体会到了前面偷的懒都是为后面挖的坑。
心得体会
在谈心得体会的时候,我首先而且必须要说的就是要摆正学习心态和学习方法。寒假里的偷懒以另一种形式增加了作业的难度,而闭门造车的这种学习方式又使得我以一种很局限的思维方式去思考,而且踩了很多没有必要的坑。而通过研讨课,讨论区,互测以及各种各样的途径,能够了解了很多优秀的设计架构,看到别人处理问题的不同方法拓展了我思考问题的角度。
不止于此,通过做本单元的作业,我也收获了很多其他层面的东西。
首先最大的收获是学习了递归下降的方法以及BNF规范的描述。
其次是快速熟悉起了java的常用类,比如ArrayList、HashMap等容器,也体会到了“不要重复造轮子”的含义,有很多基础功能是java的类中已经实现好的,直接使用即可,这样可以更专注于架构的设计,不会过于陷入细节。
最后,我体会到了面向对象编程的层次化结构,发现与面向过程的程序设计不同,学会分析问题,建立层次。把层次建立后,我们才可能去设计对象,考虑对象间的共性和个性以便建立抽象层次。面向对象的程序设计似乎更加贴近现实世界,像是在用代码描述这些对象和对象间的关系,更符合人在观察世界时的逻辑。
总之,本单元已经过去了,犯的错也无法挽回,不过前车之覆,后车之鉴,做好准备迎接电梯的到来吧!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号