LCA 的七种求法

\(2025.10.28\) upd：更新 dfs 序写法。

突然对 LCA 又感兴趣起来了，写个笔记吧。

最近公共祖先

最近公共祖先（LCA）就是这两个点的公共祖先里面，离根最远的那个。换成图就是：

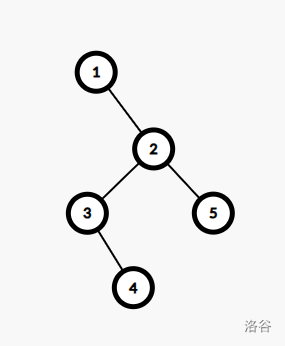
那么 \(4\) 和 \(5\) 的 LCA 就是 \(2\)。

怎么求 LCA？

好，那么我们现在知道了什么是 LCA，那么我们怎么求它呢？

方法一：暴力

俗话说得好：“遇事不决先暴力！”

所以我们可以模拟我们自己在求 LCA 时是怎么搞的。假如还是那张图：

我们已经选定求 \(4\) 和 \(5\) 的 LCA，那么我们现在要干的就是往它们的父节点上一步一步跳，直到跳到同一个点，这个点就是它们的 LCA。

为了使跳完的时候恰好跳到 LCA，我们可以找深度较大的那个点往上跳，而不是两个点一起往上。当然你可以先将两个点跳到同一个深度，然后再一起跳。

示例代码

void dfs (int u, int f) {
	dep[u] = dep[f] + 1;
	fa[u] = f;
	loop (i, head[u], nxt[i]) {//链式前向星
		int v = to[i];
		if (v == f) continue;
		dfs (v, u);
	}
}//处理出每个点的父节点和深度

int LCA (int u, int v) {
	while (u != v) {
		if (dep[u] < dep[v]) swap (u, v);
		u = fa[u];
	}//往父节点跳
	return dep[u] < dep[v] ? u : v;
}

这样做总时间复杂度（\(n\) 次查询，\(n\) 次跳跃）是 \(O(n^2)\)，模板题 P3379 显然是过不了的。

那该怎么办？如何优化？

那么接下来的方法就可以解决这个问题。

方法二：倍增

这是一个非常常用的解决树上问题的办法。

首先我们要知道一个重要性质：任意一个正整数都能被唯一分解成不相同的 \(2\) 的幂次方的形式。

证明

设有正整数 $n$，而 $k_1k_2k_3...k_p$ 是其二进制表示形式（$p=\log_2n+1$）。那么显然有 $n=\sum\limits_{i=1}^{p}k_i\cdot2^{i}$。

因为二进制累加过程中只有是 \(1\) 的数位才会累加进去，而每个 \(1\) 所在的位置唯一（这是肯定的），因此该性质成立。

所以我们在向上跳的时候，可以通过分解目标步数来降低复杂度。

具体怎么做呢？我们记 \(fa_{i,k}\) 表示点 \(i\) 向上跳 \(2^k\) 步后所到达的点。那么怎么求它呢？容易发现，一个点向上跳 \(2^k\) 步，实际上就是它向上跳 \(2^{k-1}\) 步后再向上跳 \(2^{k-1}\) 步。所以我们得到递推式：

\[fa_{i,k}=fa_{fa_{i,k-1},k-1} \]

这个可以通过 dfs 实现。

所以我们求 LCA 时，就可以利用这个数组来减少我们向上跳的步数，以此降低复杂度。我们先找深度更大的那个点，将其跳到与另一个点深度相同的点，然后两个点一起往上跳 \(2^i\) 步、\(2^j\) 步……，直到跳到同一个点为止。

（这个代码年代有点久远，所以马蜂不太一样）

示例代码

void dfs(int son,int father){
	deep[son]=deep[father]+1;
	for(int i=1;(1<<i)<=deep[son];i++){
		fa[son][i]=fa[fa[son][i-1]][i-1];//找 2^i 级祖先
	}
	for(int i=head[son];i!=-1;i=nxt[i]){
		if(father!=to[i]){
			fa[to[i]][0]=son;
			dfs(to[i],son);
		}
	}
}

int LCA(int x,int y){
	if(deep[x]<deep[y])swap(x,y);
	h=deep[x]-deep[y];
	for(int i=0;h;i++,h>>=1){
		if(h&1){
			x=fa[x][i];
		}
	}//跳到同一层
	if(x==y)return x;//y 是 x 的祖先：跳到一起当然就不跳了
	for(int i=20;i>=0;--i){
		if(fa[x][i]!=fa[y][i]){
			x=fa[x][i];
			y=fa[y][i];
		}
	}
	return fa[x][0];
}

这个方法的时间复杂度为 \(O(n\log n)\)，预处理 \(O(n\log n)\)，查询 \(O(\log n)\)，比上一个方法快多了。

AC 记录，总用时 \(1.66\) 秒。

那还有没有其他方法呢？肯定是有的！不信请继续往下看。

方法三：树链剖分（重链剖分）

这也是一个很常用的东西。

对于这个也有一个性质：对于一棵树，其重链剖分后所得到的重链数量不超过 \(\log n\)。

至于证明那就自己到网上找树链剖分的博客看吧，我绝对不会告诉你是我懒得写才不证的（实际上是不会证）。

所以我们处理出重链之后就可以直接从一个点跳到这个点所在的重链顶端，而不是一步一步往上爬，而重链最多只有 \(\log n\) 条，所以一共只会跳 \(\log n\) 次，那么时间复杂度就从暴力跳的 \(O(n)\) 降到了 \(O(\log n)\)，是一个很大的进步。

示例代码

void dfs1 (int u, int fath, int depth) {
	dep[u] = depth, fa[u] = fath, siz[u] = 1;
	for (int i = head[u]; i != -1; i = nxt[i]) {
		int v = to[i];
		if (v == fath) continue;
		dfs1 (v, u, depth + 1);
		siz[u] += siz[v];
		if (siz[son[u]] < siz[v]) son[u] = v;//找重儿子
	}
}//处理每一个点的深度、父节点和重儿子

void dfs2 (int u, int t) {
	id[u] = ++ cnt, tp[u] = t;
	if (!son[u]) return ;
	dfs2 (son[u], t);
	for (int i = head[u]; i != -1; i = nxt[i]) {
		int v = to[i];
		if (v == fa[u] || v == son[u]) continue;
		dfs2 (v, v);
	}
}//处理每一个点的 dfs 序和所在的重链的顶端

ll LCA (int u, int v) {
	while (tp[u] != tp[v]) {
		if (dep[tp[u]] < dep[tp[v]]) swap (u, v);
		u = fa[tp[u]];
	}
	if (dep[u] < dep[v]) swap (u, v);
	return v;
}//求 LCA

这个方法的复杂度也是 \(O(n\log n)\) 的，预处理 \(O(n)\)，查询 \(O(\log n)\)，但是常数比倍增大（可模板题跑的比倍增快）。

AC 记录，总时间 \(1.52\) 秒。

那么现在又有人说了：你这查询都是 \(O(\log n)\)，这难道就是极限了？谁给你说的，人类的智慧可是无穷无尽的。

方法四：欧拉序

参考了《使用欧拉序 st 表 O(1) 求 LCA》一文。

容易发现，在求 LCA 时，一般整个树的形态是不会发生改变的，也就是说这是一个静态查询问题。有没有觉得灵光乍现？没错，RMQ 问题也是这样的。那么我们是否可以借用解决 RMQ 问题的 ST 表呢？当然是行的。不过我们还需借助欧拉序。

什么是欧拉序呢？仍然是那张图：

它的欧拉序就是对整棵树 dfs 所经过的点与回溯到的点所组成的序列。那么这棵树的欧拉序就是 \(1-2-3-4-3-2-5-2-1\)。

接下来思考如何求 LCA。假如说我们要求 \(3\) 和 \(5\) 的 LCA，那么我们先把 \(3\) 和 \(5\) 在欧拉序中第一次出现的位置打个标记：

\[1-2-\color{red}3-\color{blue}4-3-2-\color{red}5\color{black}-2-1 \]

容易发现，\(3\) 和 \(5\) 的 LCA 就是上面标蓝的点中深度最小的点（也就是 \(2\)）。所以我们可以直接遍历整个欧拉序，找到两个点第一次出现的位置，再找到他们之间深度最小的点是哪个。

骗你的，这样肯定直接起飞。由于树的形态不变，那么欧拉序也不会变，所以我们可以用 ST 表来优化。设 \(st_{i,j}\) 表示欧拉序中第 \(i\) 个点及其后面共 \(2^j\) 个点中深度最小的点，然后用 ST 表的预处理方法去搞就行了。

示例代码

void dfs (int u, int fa) {
	id[u] = ++ tot;
	pot[tot] = u;
	dep[u] = dep[fa] + 1;
	loop (i, head[u], nxt[i]) {
		int v = to[i];
		if (v == fa) continue;
		dfs (v, u);
		pot[++ tot] = u;
	}
}//处理欧拉序

void init () {
	dfs (rt, 0);
	for (int i = 1; i <= tot; ++ i) {
		st[i][0] = pot[i];
		if (i > 1) lg[i] = lg[i >> 1] + 1;
	}
	for (int j = 1; j <= lg[tot]; ++ j) {
		for (int i = 1; i + (1 << j) - 1 <= tot; ++ i) {
			int u = st[i][j - 1], v = st[i + (1 << j - 1)][j - 1];
			st[i][j] = dep[u] < dep[v] ? u : v;//找深度更小的点
		}
	}
}//处理 ST 表

int LCA (int u, int v) {
	if (id[u] > id[v]) swap (u, v);
	u = id[u], v = id[v];
	int k = lg[v - u + 1];
	u = st[u][k], v = st[v - (1 << k) + 1][k];
	return dep[u] < dep[v] ? u : v;
}//求 LCA

方法五：dfs 序

参考了冷门科技 —— DFS 序求 LCA这篇文章。

跟上面的方法一样，只不过是将欧拉序改成了 dfs 序。

首先我们肯定需要求出一棵树的 dfs 序。

假设我们当前要求的是 \(u\) 和 \(v\) 的 LCA，而他们的 LCA 为 \(f\)，我们钦定 \(dfn_u < dfn_v\)，这样会比较好讨论（因为不会出现 \(u\) 是 \(v\) 的 儿子的情况）。

那么接下来开始讨论。

1. 若 \(u\) 不是 \(v\) 的祖先，那么 dfs 的时候一定会以 \(f\rightarrow u\rightarrow f\rightarrow v\) 的顺序进行遍历。由此可以发现，\(dfn_u\) 和 \(dfn_v\) 之间的所有点一定在 \(f\) 的子树内（其实比较显然，可以自己动手画画看）。我们再设 \(v'\) 为 \(f\rightarrow v\) 方向上的第一个点，那么 \(v'\) 的子树一定是包含 \(v\) 的，根据 dfs 的顺序，\(dfn_{v'}\) 一定在 \([dfn_u,dfn_v]\) 之间，并且 \(v'\) 的深度最小，所以我们只需要找到 \([dfn_u,dfn_v]\) 之间深度最小的那个点，他的父亲即为 \(u\) 和 \(v\) 的 LCA。
2. 若 \(u\) 是 \(v\) 的祖先，那么我们就把查询区间改为 \([dfn_u+1,dfn_v]\)。对于情况 \(1\)，\(u\not=v'\)，所以我们仍可以按照情况 \(1\) 的方法去做。

所以说，当 \(u\not=v\) 时，我们只需找到 \([dfn_u,dfn_v]\) 之间深度最小的那个点的父亲；当 \(u=v\) 时，显然 LCA 为 \(u\)（注意：要特判这种情况）。

示例代码

int get (int x, int y) { return id[x] < id[y] ? x : y; }

void dfs (int u, int fa) {
    id[u] = ++ tot;
    st[0][id[u]] = fa;
    dep[u] = dep[fa] + 1;
    for (int i = head[u]; ~i; i = nxt[i]) {
        int v = to[i];
        if (v == fa) continue;
        dfs(v, u);
    }
}//预处理 dfs 序

void init () {
    dfs (rt, 0);
    for (int i = 1; i <= 21; ++ i)
        for (int j = 1; j + (1 << i) - 1 <= tot; ++ j)
            st[i][j] = get(st[i - 1][j], st[i - 1][j + (1 << (i - 1))]);
}//预处理 ST 表

int LCA (int u, int v) {
    if (u == v) return u;//注意特判
    int x = id[u], y = id[v];
    if (x > y) swap (x, y);
    int d = log2 (y - x);
    x ++;//变成父亲
    return get (st[d][x], st[d][y - (1 << d) + 1]);
}//求 LCA

哇，这两个方法的总时间复杂度竟然也是 \(O(n\log n)\)！虽然预处理仍然是 \(O(n\log n)\)，但是查询做到了 \(O(1)\)！而且常数也是最小的（dfs 序的超级小）。但是空间开销比上面两种都大。

AC 记录（欧拉序），时间 \(1.74\) 秒（怎么更慢了）。

AC 记录（dfs 序），时间 \(869\) 毫秒（不是怎么比 \(O(n)\) 的 Tarjan 还快）。

喜欢挑刺的人又来了：“你这预处理的 \(O(n\log n)\) 还是不够优秀，还有更优的吗？”怎么会没有，这不就来了吗！

方法六：Tarjan

参考了《trajan算法求lca 超级详细配图讲解》一文。

这是一个离线求 LCA 的方法。

我们首先将询问离线，然后将每个询问反着复制一份（就比如查 \(4\) 和 \(5\) 的 LCA 就在填一份查 \(5\) 和 \(4\) 的 LCA，至于为什么要这样后面会说），接着带着询问去 dfs 整棵树。如果我们遍历到的这个点是查询中的，并且我们已经记录了它的信息，我们就将答案保存。如何判断是否记录了它的信息呢？我们设 \(vis_i\) 表示 \(i\) 号点现在遍历的状态，具体的：

• 当 \(vis_i=0\) 时，表示 \(i\) 未被遍历到。我们称其为“白点”。
• 当 \(vis_i=1\) 时，表示 \(i\) 被遍历了一次。我们称其为“红点”。
• 当 \(vis_i=2\) 时，表示 \(i\) 被遍历了两次，即已经回溯。我们称其为“黑点”。

可以发现，\(i\) 和 \(j\) 的 LCA 就是 \(i\) 和 \(j\) 的所有被染成红点的公共祖先中深度最大的那个，也就是它们往上跳的时候遇到的第一个红点。（可以自己手推一下，或者上网看证明）

但是，直接暴力的找深度最大的点肯定起飞，我们如何快速找到那个点呢？

我们可以在回溯的过程中将 \(i\) 点的父亲指针指向其直接父节点，然后是父亲的父亲节点……一直指到 LCA。具体来说，这个过程实制上是通过并查集来实现 “路径压缩” 的效果：当我们从子节点回溯到父节点时，会把这个子节点的父指针直接改成当前的父节点 —— 因为子节点已经处理完毕（变成黑点），它的 “最近红点祖先” 不再是自己，而是仍处于红点状态的父节点。

比如，假设节点 \(b\) 是节点 \(a\) 的子节点，当 \(a\) 还在遍历（红点）、\(b\) 已经回溯（黑点）时，我们就把 \(b\) 的父指针从原本指向自己（或更浅的祖先）改为指向 \(a\)。这样一来，当 \(b\) 需要向上找红点祖先时，就会直接跳到 \(a\)，省去了中间的无效查找，节省了大量时间。以此类推，当 \(a\) 也回溯时，它的父指针会指向它的父节点（比如 \(c\)，此时仍是红点），那么 \(b\) 再通过父指针跳转时，就会先到 \(a\)，再由 \(a\) 的父指针跳到 \(c\)……最终形成一条从黑点直接通往 “最深红点祖先” 的路径。

所以当处理查询时，比如遇到点 \(u\) 是黑点、点 \(v\) 是红点的情况，我们只需要让 \(u\) 顺着父指针不断向上跳，第一个遇到的红点就是 \(u\) 和 \(v\) 的所有公共祖先中深度最大的那个，也就是它们的 LCA。这种通过回溯动态调整父指针的方式，把原本需要遍历整条祖先链的暴力查找，优化成了近乎 “一步直达” 的高效操作，避免了时间复杂度的爆炸。

至于复制查询的作用，是为了确保无论 dfs 先遍历到 \(u\) 还是 \(v\)，总会出现“一个是黑点、一个是红点”的场景，此时借助这种优化后的父指针跳转，就能稳定地找到 LCA 了。

示例代码

void Tarjan (int u) {
	vis[u] = 1;
	loop (i, head[u], nxt[i]) {
		int v = to[i];
		if (vis[v]) continue;//访问过
		Tarjan (v);
		fa[v] = u;//合并并查集
	}
	for (auto x : q[u]) {
		int y = x.to, id = x.id;
		if (vis[y] == 2) ans[id] = find (y);//已经回溯就统计答案
	}
	vis[u] = 2;//已回溯
}

int main () {
  /*读入省略....*/
	for (int i = 1, u, v; i <= m; ++ i) {
		read (u, v);
		if (u == v) {
			ans[i] = u;
			continue;
		}
		q[u].pb ({v, i});
		q[v].pb ({u, i});//复制询问
	}
	Tarjan (rt);
    for (int i = 1; i <= m; ++ i) printf ("%d\n", ans[i]);
	return 0;
}

这个方法总时间复杂度 \(O(n)\)，预处理 \(O(n)\)，查询 \(O(1)\)，非常优秀。

AC 记录，总用时 \(1.29\) 秒。

以上就是常规的求 LCA 的方法。接下来的方法相对来说就不是那么常规了。

方法七：分块

你没看错，LCA 可以根号复杂度求出。

以下参考了这篇题解。

这个方法是受 P7446 的启发搞出来的。我们对每个点的父节点所组成的序列进行分块。设 \(pa_i\) 表示当前点跳出这个块的第一个祖先，\(fa_i\) 表示这个点的祖先节点。那么我们再定义两个操作：小跳表示在块内跳祖先节点（即 \(i\leftarrow fa_i\)），大跳表示在块间跳父节点（即 \(i\leftarrow pa_i\)），那么求 LCA 就等于是重复以下操作，直到两个点相同：

1. 如果两个点大跳后不在同一块，或者两点大跳后同块不同点，那么就让祖先编号大的大跳。
2. 如果上面的都不满足，就让编号大的小跳。

当两个点跳到同一个点时，这个点即为 LCA（其实和树剖挺像的，而且支持父节点的修改）。

示例代码

void build_fa (int u, int f) {
    fa[u] = f;
    dep[u] = dep[f] + 1;
    loop (i, head[u], nxt[i]) {
        int v = to[i];
        if (v != f) build_fa (v, u);
    }
}//找每个点的父节点（因为根节点确定，所以一定能找到）

void initpa () {
	for (int p = 1; p <= t; ++ p) {
		for (int i = l[p]; i <= r[p]; ++ i) {
			int P = fa[i];
			pa[i] = (P >= l[p] && P <= r[p]) ? pa[P] : P;
		}
	}
}//处理每个点跳出这个块的第一个祖先

void init () {
	t = (n + BS - 1) / BS;
	for (int i = 1; i <= t; ++ i) {
		l[i] = r[i - 1] + 1;
		r[i] = min (l[i] + BS - 1, n);
		for (int j = l[i]; j <= r[i]; ++ j) pos[j] = i;
	}
	initpa ();
}//分块

int LCA (int u, int v) {
	while (u != v) {
		if (pos[u] != pos[v]) {
			if (dep[pa[u]] < dep[pa[v]]) swap (u, v);
			u = pa[u];
		} else {
			if (dep[u] < dep[v]) swap (u, v);
			u = fa[u];
		}
	}
	return u;
}//如上所言

这个方法的时间复杂度是除暴力外最劣的，为 \(O(n\sqrt n)\)，预处理 \(O(n)\)，查询 \(O(n\sqrt n)\)。对于模板题 \(5\times10^5\) 的数据肯定是过不了的（但是为什么这份代码连暴力都跑不过啊）。

至此，LCA 的七种求法就介绍完了，如有错误还请私信我，谢谢。