视图变换矩阵和投影变换矩阵

变换

3D -> 2D

2D空间的变换

1. 缩放变换

\[\begin{bmatrix}x'\\ y'\\ \end{bmatrix}= \begin{bmatrix}s & 0\\0 & s\\ \end{bmatrix} \begin{bmatrix}x\\ y\\ \end{bmatrix} \]

2. 反射变换--以坐标轴翻转

\[\begin{bmatrix}x'\\ y'\\ \end{bmatrix}= \begin{bmatrix}-1 & 0\\0 & 1\\ \end{bmatrix} \begin{bmatrix}x\\ y\\ \end{bmatrix} \]

3. 剪切变换
   假设沿着x轴正向剪切，在y高度上，每个等高线上的点沿着x轴正向移动的距离是a*y，a为y=1时x的移动距离

\[\begin{bmatrix}x'\\ y'\\ \end{bmatrix}= \begin{bmatrix}1 & a\\0 & 1\\ \end{bmatrix} \begin{bmatrix}x\\ y\\ \end{bmatrix} \]

4. 旋转变换
   默认绕原点逆时针旋转\(\alpha\)度

\[\begin{bmatrix}x'\\ y'\\ \end{bmatrix}= \begin{bmatrix}cos\alpha & -sin\alpha\\ sin\alpha & cos\alpha\\ \end{bmatrix} \begin{bmatrix}x\\ y\\ \end{bmatrix} \]

使用齐次坐标表示变换矩阵

方便解决平移矩阵
2D变换矩阵 -> 3D变换矩阵

\[\begin{bmatrix} a & b \\ c & d \end{bmatrix} -> \begin{bmatrix} a & b & t_x\\ c & d & t_y \\ 0 & 0 & 1 \end{bmatrix} \]

\(t_x,t_y\)就表示平移的移动量
同样对于2D平面内的点或者向量，也需要变为3D坐标表示，对于点可以在末尾加1即可，对于向量可以在末尾加0即可。
点：(x,y) -> (x,y,1)
向量：(x,y) -> (x,y,0)

3D空间变换

与2D平面相同，从3D->4D
点：(x,y,z) -> (x,y,z,1)
向量： (x,y,z) -> (x,y,z,0)

\[\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} -> \begin{bmatrix} a & b & c & t_x\\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

欧拉角

处理3D空间中绕任意轴的旋转问题，将该轴求解出与坐标轴的角度关系
\(R_{xyz}(\alpha,\beta,\gamma) = R_x({\alpha})+R_y(\beta)+R_z(\gamma)\)

MVP矩阵

1. Model Trans Matrix -> 对物体实际位置的变换
2. View Trans Matrix -> 对相机的变换
3. Proj Trans Matrix -> 3D->2D

Viewing Trans

View Trans 视图变换

对相机位置和朝向的确定。
需要三个向量

1. 相机位置 e
2. 朝向 lookat g
3. 向上方向 up direction l

物体如果和相机保持相对静止，那么相机的所看到的物体是一样的。
所以约定
1. 相机位置在原点，相机的朝向是-z，相机的向上方向是y

所以视图变换就是将相机位置(x,y,z)移动到(0,0,0)，并旋转朝向向量和向上向量
g 旋转到 -z l 旋转到y (g×l)旋转到x
考虑从x轴，y轴，z轴旋转到g×l，l，g的矩阵。
而反过来旋转就是该矩阵的逆，也即是视图变换矩阵的旋转模块。而由于旋转矩阵是正交矩阵，所以逆就是矩阵的转置。
然后对于空间中的物体，也需要应用该矩阵实现物体的变换。

Proj Trans 投影变换

近大远小 或者 近远相同

正交变换

近远相同，对于处在约定位置的相机观测出来的图像，将物体的z值去掉，即得到投影结果。
定义空间中一个立方体[l,r]×[b,t]×[f,n]，这个立方体是观测物体的包围和。然后将这个包围盒变换为中心为原点的单位立方体，可以通过平移和缩放矩阵
l,r表示在x轴上的左边界和右边界，b,t表示在y轴上的底和顶，f,n表示在z轴上的前面和后面（由于摄像机是朝z负方向的）

\[M_{ortho} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

透视变换

近大远小

第一种方法

GAMES101
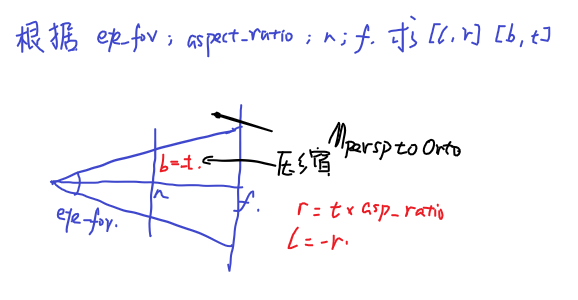
压缩除了n平面的所有平面，将其他平面压缩，直到整个锥体变为长方体\(M_{persp->ortho}\)
所以压缩后，x,y两值就变换为下式

\[x = \frac{nx}{z}\\ y = \frac{ny}{z} \]

此时可以初步写出\(M_{persp->ortho}\)除了第三行的矩阵

\[\begin{bmatrix}n & 0 & 0 & 0\\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{bmatrix} \]

由于压缩变换不会改变z的值。那么对于变换后的值\(\begin{bmatrix}\frac{nx}{z} \\ \frac{ny}{z} \\ z \\ 1 \end{bmatrix} == \begin{bmatrix}nx \\ ny \\ z^2 \\ z \end{bmatrix}\)
可以推断出第三行格式为(0,0,A,B)
将z分别使用近平面值n和远平面值f带入即可求得两个参数

\[(0,0,A,B) * \begin{bmatrix}x \\ y \\ n \\ 1 \end{bmatrix} == An + B == n^2\\ (0,0,A,B) * \begin{bmatrix}x \\ y \\ f \\ 1 \end{bmatrix} == Af + B == f^2 \]

求解即得到A ,B值。

\[A = n+f \\ B = -nf \]

然后现在锥体就变为了长方体，再使用正交投影的矩阵相乘，即得到透视投影的变换矩阵
\(M_{persp} = M_{persp->ortho} * M_{ortho}\)

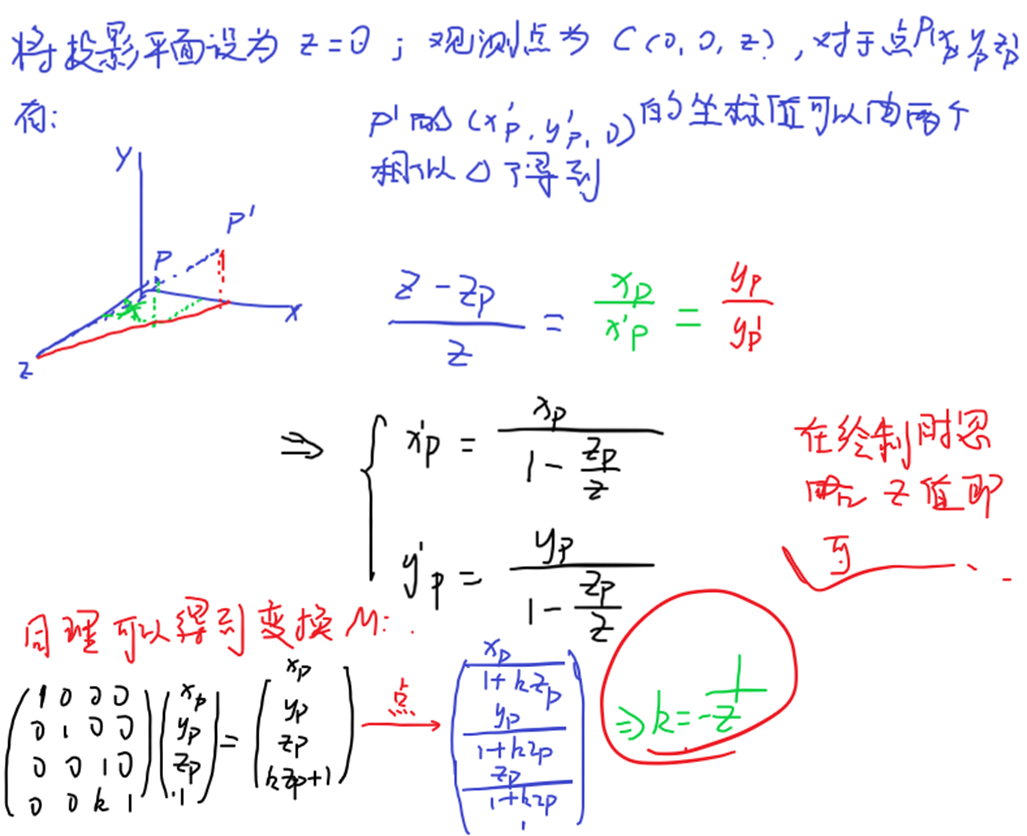
第二种方法

tinyrender