P3103 [USACO14FEB] Airplane Boarding G 做题记录

P3103 [USACO14FEB] Airplane Boarding G

Description

https://www.luogu.com.cn/problem/P3103

Solution

考虑将奶牛的移动刻画成折线。

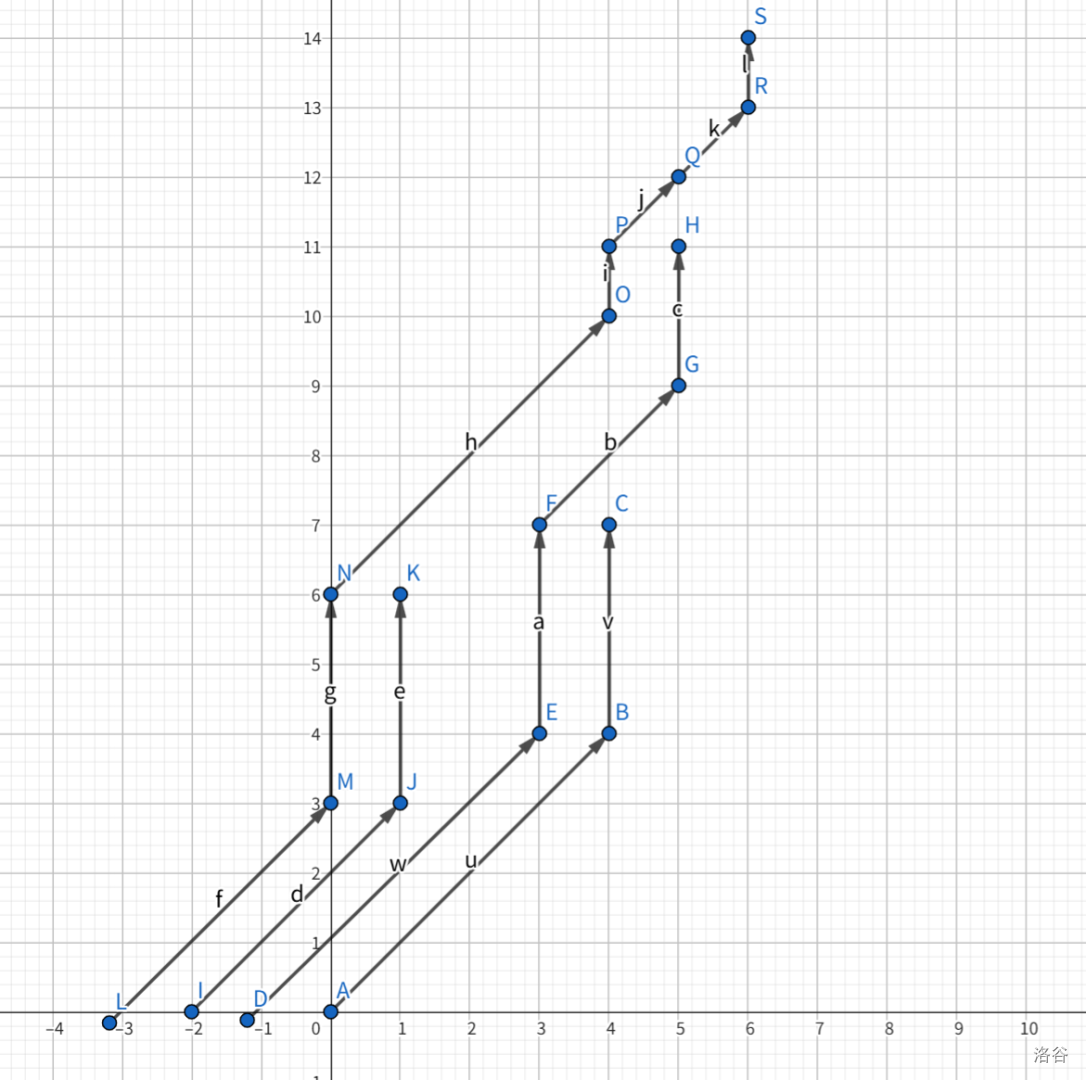
每一只奶牛的折线都不能与之前的奶牛重合。

观察一下，斜向上的折线不会对后面的奶牛造成任何影响，所以只需要保留竖直的折线。

我们把这些竖直的折线抽象为一个二元组 \((s_j,t_j)\)，表示时刻 \(t_j\) 之后才可以到达 \(s_j\)。

那么奶牛 \(i\) 到达终点 \(x_i\) 的时间 \(v_i\) 即为 \(\max\{x_i-s_j+t_j\}\)，即 \(x_i-\max\{t_j-s_j\}\)。于是只需要维护一段前缀的 \(t_j-s_j\) 的最大值。到达终点后，会增加一条 \((x_i,v_i+1)\) 的竖直折线。

观察折线图，奶牛 \(i\) 经过 \((s_j,t_j)\) 这条线后，会新增一个 \((s_j-1,t_j)\) 的竖直折线。相当于对一段前缀的 \(s_i\) 全部减一。

需要支持单点插入、区间加、区间 \(\max\)，平衡树维护。时间复杂度 \(O(n\log n)\)。

int n,s[N],t[N];

mt19937 rnd(time(0));

struct FHQ_Treap{
    int lc,rc,pri;
    int key,val,mx,add;
}tr[N];

int tot,root;

int NewNode(int x,int y){
    tr[++tot]={0,0,(signed)rnd(),x,y,y,0};
    return tot;
}

void Add(int p,int v){
    tr[p].key-=v;
    tr[p].val+=v;
    tr[p].mx+=v;
    tr[p].add+=v;
}

void Spread(int p){
    if(!tr[p].add) return;
    if(tr[p].lc) Add(tr[p].lc,tr[p].add);
    if(tr[p].rc) Add(tr[p].rc,tr[p].add);
    tr[p].add=0;
}

void Pushup(int p){
    tr[p].mx=max({tr[p].val,tr[tr[p].lc].mx,tr[tr[p].rc].mx});
}

void Split(int p,int v,int &L,int &R){
    if(!p) return L=R=0,void();
    Spread(p);
    if(tr[p].key<=v) L=p,Split(tr[p].rc,v,tr[p].rc,R);
    else R=p,Split(tr[p].lc,v,L,tr[p].lc);
    Pushup(p);
}

int Merge(int p,int q){
    if(!p) return q;
    if(!q) return p;
    if(tr[p].pri>tr[q].pri){
        Spread(p);
        tr[p].rc=Merge(tr[p].rc,q);
        return Pushup(p),p;
    }
    else{
        Spread(q);
        tr[q].lc=Merge(p,tr[q].lc);
        return Pushup(q),q;
    }
}

int Ask(int v){
    int L,R,res;
    Split(root,v,L,R);
    res=tr[L].mx;
    root=Merge(L,R);
    return res;
}

void Insert(int x,int y){
    int L,R,M=NewNode(x,y);
    Split(root,x,L,R);
    root=Merge(Merge(L,M),R);
}

void Update(int v){
    int L,R;
    Split(root,v,L,R);
    Add(L,1);
    root=Merge(L,R);
}

signed main(){
    read(n);
    for(int i=1;i<=n;i++) read(s[i]),read(t[i]);
    reverse(s+1,s+n+1);
    reverse(t+1,t+n+1);
    int ans=0;
    for(int i=1;i<=n;i++){
        int res=max(s[i]+t[i]+i-1,s[i]+t[i]+Ask(s[i]));
        Ckmax(ans,res);
        Update(s[i]);
       Insert(s[i],res+1-s[i]);
    }
    printf("%lld\n",ans);
    return 0;
}