连分数 与 Stern-Brocot-Tree

连分数 与 Stern-Brocot-Tree

I. 连分数

1. 基本概念

形如 \(a_0+\dfrac{1}{a_1+\dfrac{1}{a_2+\dfrac{1}{\cdots+\dfrac 1 {a_n}}}}\) 的分数称为 连分数，记为 \([a_0,a_1,a_2,a_3,\cdots，a_n]\)。

我们主要研究的是 \(a_i\) 为整数的连分数。

对于连分数 \(x=[a_0,a_1,a_2,\cdots,a_n]\)，称 \(x_k=[a_0,a_1,\cdots,a_k] \ (0\leq k\leq n)\) 为 \(x\) 的第 \(k\) 个 渐进分数，\(r_k=[a_k,a_{k+1},\cdots,a_n]\) 为 \(x\) 的第 \(k\) 个 余项。

\(x_n\) 即 \(x\) 本身。当 \(k\) 逐渐增大时，\(x_k\) 逐渐逼近 \(x\)。

容易得到，\(x+k=[a_0+k,a_1,a_2,\cdots,a_n]\)，\(x^{-1}=[0,a_0,a_1,a_2,\cdots,a_n]\)。

2. 有理数的连分数表示

对于任意有理数 \(x\)，有且仅有两种连分数表示形式：

\[[a_0,a_1,a_2,\cdots,a_n] \]

\[[a_0,a_1,a_2,\cdots,a_n-1,1]. \]

例如，\(\dfrac 3 2=1+\dfrac 1 2=1+\dfrac 1 {1+\dfrac 1 1}\)。

末项为 \(1\) 的表示方法称为 非标准表示，末项不为 \(1\) 的称为 标准表示。

考虑对于任意的有理数 \(\dfrac p q\)，求出其连分数表示，其中 \(p,q\) 均为正整数。

设 \(\dfrac p q=x=[a_0,a_1,a_2,\cdots,a_n]\)。

由连分数的定义，若 \(r_k\) 不为整数，则有

\[a_k=\lfloor r_k \rfloor,r_{k+1}=\dfrac 1 {r_k-a_k}. \]

设 \(r_k=\dfrac{p_k}{q_k}\)，得

\[a_k=\lfloor\dfrac{p_k}{q_k} \rfloor,r_{k+1}=\dfrac{1}{\dfrac {p_k}{q_k}-a_k}=\dfrac{q_k}{p_k-a_kq_k}=\dfrac{q_k}{p_k\bmod q_k}. \]

类似于辗转相除法，令 \(r_0=\dfrac p q\)，我们递归求出每个 $a_i $，直到 \(q=0\) 时停止。时间复杂度 \(O(\log(\min(p,q)))\)。

3. 渐进分数的递推关系

对于连分数 \(x=[a_0,a_1,a_2,\cdots，a_n]\)，设 \(x_k=\dfrac{p_k}{q_k}\)。特别地，令 \(x_{-2}=\dfrac 0 1,x_{-1}=\dfrac 1 0\)。

\(p_k,q_k\) 之间有递推关系：

\[p_k=a_kp_{k-1}+p_{k-2} \]

\[q_k=a_kq_{k-1}+q_{k-2}. \]

证明：数学归纳法。当 \(k = 0\) 时显然成立。

假设对于 \(k-1\) 成立。

首先 \(x_k=[a_0,a_1,a_2,\cdots，a_{k-1},a_{k}]=[a_0,a_1,a_2,\cdots，a_{k-1}+\dfrac 1 {a_{k}}]\)。

于是 \(x_k=\dfrac{(a_{k-1}+\dfrac 1 {a_{k}})p_{k-2}+p_{k-3}}{(a_{k-1}+\dfrac 1 {a_{k}})q_{k-2}+q_{k-3}}=\dfrac{a_{k-1}p_{k-2}+\dfrac{p_{k-2}}{a_k}+p_{k-3}}{a_{k-1}q_{k-2}+\dfrac{q_{k-2}}{a_k}+q_{k-3}}=\dfrac{p_{k-1}+\dfrac{p_{k-2}}{a_k}}{q_{k-1}+\dfrac{q_{k-2}}{a_k}}=\dfrac{a_kp_{k-1}+p_{k-2}}{a_kq_{k-1}+q_{k-2}}\)。

II. Stern-Brocot-Tree

1. 基本概念

Stern-Brocot-Tree 是一棵包含所有正有理数的二叉树，简称为 SBT。

我们用三元组 \((\dfrac a b,\dfrac x y,\dfrac c d)\) 来构建 SBT，其中有 \(\dfrac x y=\dfrac{a+c}{b+d}\)。

SBT 以 \((\dfrac 0 1,\dfrac 1 1,\dfrac 1 0)\) 为根。对于一个节点 \((\dfrac a b,\dfrac x y,\dfrac c d)\)，其左儿子为 \((\dfrac a b,\dfrac {a+x}{b+y},\dfrac x y)\)，右儿子为 \((\dfrac x y,\dfrac {x+c}{y+d},\dfrac c d)\)。

在节点 \((\dfrac a b,\dfrac x y,\dfrac c d)\) 中，称 \(\dfrac x y\) 为 \(\dfrac a b,\dfrac c d\) 的中位分数。

SBT 节点实际存储的分数是中位分数，两边的端点可以看作附加信息。

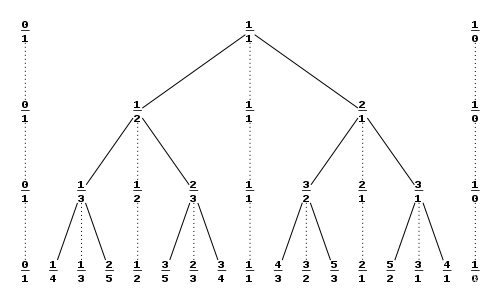
2. 性质

Property 1： 每个在 SBT 中的节点 \((\dfrac a b,\dfrac {a+c}{b+d},\dfrac c d)\)，满足 \(bc-ad=1\)。

数学归纳法。根节点显然成立。

假设对于节点 \((\dfrac a b,\dfrac {a+c}{b+d},\dfrac c d)\)，\(bc-ad=1\) 成立。

考虑其左儿子 \((\dfrac a b,\dfrac {2a+c}{2b+d},\dfrac {a+c}{b+d})\)，\(b(a+c)-a(b+d)=bc-ad=1\)。

考虑其右儿子 \((\dfrac {a+c}{b+d},\dfrac{a+2c}{b+2d},\dfrac c d)\)，\((b+d)c-d(a+c)=bc-ac=1\)。

Property 2： 每个在 SBT 中出现的分数一定是最简的。

数学归纳法。根节点显然成立。

考虑节点 \((\dfrac a b,\dfrac {a+c}{b+d},\dfrac c d)\)。

由 Property 1，\(b(a+c)-a(b+d)=1\)，即关于 \(x,y\) 的不定方程 \(x(a+c)+y(b+d)=1\) 有整数解。

由裴蜀定理，\(\gcd(a+c,b+d)=1\)。即 \(\dfrac {a+c}{b+d}\) 为最简分数。

Property 3： SBT 中每一层的分数单调递增。

等价于对于任意一个节点 \((\dfrac a b,\dfrac {a+c}{b+d},\dfrac c d)\)，有 \(\dfrac a b<\dfrac {a+c}{b+d}<\dfrac c d\)。易证。

Property 4： SBT 是一棵二叉搜索树。

由 Property 3 易证。

Property 5： 任意一个正有理数在 SBT 中恰好出现一次。

由 Property 3，任意一个正有理数在 SBT 中最多出现一次。

下面只需证明，任意一个正有理数在 SBT 中至少出现一次。

假设已知 \(\dfrac a b<\dfrac p q<\dfrac c d\)。得到 \(bp-aq>0,cq-dp>0\)，即 \(bp-aq\geq 1,cq-dp\geq 1\)。

两个不等式两边分别乘 \(c+d,a+b\)，得到 \((c+d)(bp-aq)+(a+b)(cq-dp)\geq a+b+c+d\)。

整理得 \((bc-ad)(p+q)=p+q\geq a+b+c+d\)。

我们从根节点开始，根据 \(\dfrac p q\) 与 \(\dfrac {a+c}{b+d}\) 的大小关系决定向哪一个儿子走。

等式右边 \(a+b+c+d\) 不断增加，即一定能在有限步数内找到 \(\dfrac p q\)。

III. SBT 与 连分数

1. 知分数求路径

我们从根开始，左右交替移动端点。

不妨假设首组移动是向右的；如果不然，则设首组向右移动的次数为零。将每组移动后的端点位置排列如下：

\[\frac{p_0}{q_0}, \frac{p_1}{q_1}, \frac{p_2}{q_2}, \dots, \frac{p_{n-2}}{q_{n-2}}, \frac{p_{n-1}}{q_{n-1}}, \frac{p_n}{q_n}. \]

其中，偶数组移动是向右的，故而记录的是左端点的位置；奇数组移动是向左的，故而记录的是右端点的位置。在这一列端点前面再添加两个端点

\[\frac{p_{-2}}{q_{-2}} = \frac{0}{1}, \frac{p_{-1}}{q_{-1}} = \frac{1}{0}. \]

设第 \(k\) 组移动的次数为 \(t_k\)，那么根据上面得到的移动次数与端点位置之间的关系可知

\[\frac{p_k}{q_k} = \frac{t_k p_{k-1} + p_{k-2}}{t_k q_{k-1} + q_{k-2}}. \]

由连分数的 递推关系，

\[\frac{p_k}{q_k} = [t_0, t_1, \cdots, t_k]. \]

最后我们得到

\[\frac{p}{q} = \frac{p_k + p_{k-1}}{q_k + q_{k-1}} = [t_0, t_1, \cdots, t_{n-1}, t_n, 1]. \]

因此，在目标分数的末尾为一的 连分数表示 中，不计最后的一，前面的项就编码了 Stern-Brocot 树上自根节点到当前节点的路径。偶数项（下标自 0 开始）向右，奇数项向左。

设 \(\dfrac p q=[a_0,a_1,a_2,\cdots,a_n,1]\)。有推论：

1. 若 \(a_n>1\)，则其父节点为 \([a_0,a_1,a_2,\cdots,a_n-1,1]\)；否则即为 \([a_0,a_1,a_2,\cdots,a_{n-1},1]\)。
2. 其两个子节点分别为 \([a_0,a_1,a_2,\cdots,a_n,1,1],[a_0,a_1,a_2,\cdots,a_n+1,1]\)。

2. 知路径查分数

先将路径化为连分数的形式，设为 \([a_0,a_1,a_2,\cdots,a_n]\)。那么要求的分数就是 \([a_0,a_1,a_2,\cdots,a_n,1]\)。

注意，如果路径第一步是向左的，要在路径序列最前面添一个 \(0\)。