双连通图性质

双连通图性质

约定：下面讨论的点双 都不是 “两点一线”，即点的个数 \(\geq 3\)。

Property 1

点双内所有点的度数均 \(\geq 2\)。

否则，设 \(x\) 只有 \((x,y)\) 这一条出边，删去 \(y\) 后 \(x\) 与其他点不连通。

同理，边双内所有点度数也 \(\geq 2\)。

Property 2

点双一定是边双。

假设点双内存在一条割边为 \((u,v)\)。由于 \(u,v\) 的度数都 \(\geq 2\)，删去 \(u\) 或 \(v\)，图会不联通，与点双定义矛盾。

唯一的特例是 “两点一线”。

但边双不一定是点双，如图：

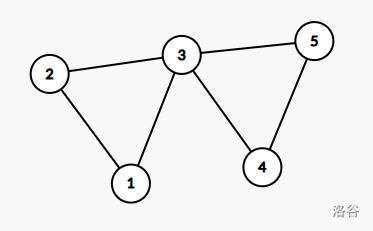
Property 3

对于点双内任意一点 \(x\)，一定存在经过 \(x\) 的简单环。

删去 \(x\) 后，剩余部分连通。

找出 \(x\) 的两条出边 \((x,y),(x,z)\) 其中 \(y\ne z\)。

\(y,z\) 之间在新图中一定有一条路径，拼上 \(x\) 即为一个简单环。

对于边双内任意一点 \(x\)，一定存在经过 \(x\) 的简单环。

找到 \(x\) 的一条出边 \((x,y)\) 并将其删除，剩下部分仍然联通。

新图中 \(x,y\) 之间一定有一条路径，拼上 \((x,y)\) 即为一个简单环。

Property 4

对于点双 \(G_1\) 内任意一条边 \((u,v)\)，删去这条边，加入一个新点 \(w\) 与两条新边 \((u,w),(w,v)\)，新图 \(G_2\) 仍然点双连通。

在 \(G_1\) 中删去 \(u,v\) 得到新图 \(G_3\)，\(G_3\) 联通，加上点 \(w\) 仍然联通，则 \(G_2\) 中 \(u,v\) 都不是割点。

由于 \(G_1\) 中 \((u,v)\) 不是割边，则 \(w\) 在 \(G_3\) 中不是割点。

显然其他的点在 \(G_3\) 中也不会变为割点。

对于边双 \(G_4\) 内任意一条边 \((u,v)\)，删去这条边，加入一个新点 \(w\) 与两条新边 \((u,w),(w,v)\)，新图 \(G_5\) 仍然边双连通。

\((u,v)\) 在 \(G_4\) 中不是割边，则 \((u,w),(w,v)\) 在 \(G_5\) 中也不是割边。

其他的边在 \(G_5\) 中也不会变为割边。

Property 5

对于点双内任意两点 \(x,y\)，存在两条点不相交的简单路径。

这也就等价于，对于点双内任意两点 \(x,y\)，存在一个包含 \(x,y\) 的简单环。

这个证明需要用到 门杰定理 相关内容，我还不会

对于边双内任意两点 \(x,y\)，存在两条边不相交的简单路径。

等价于对于边双内任意两点 \(x,y\)，存在一个包含 \(x,y\) 的回路。

同上。

Property 6

对于点双内任意一点 \(x\) 与任意一条边 \((u,v)\)，存在一个包含 \(x,(u,v)\) 的简单环。

删去 \((u,v)\)，加入 \((u,w),(w,v)\)。由性质 4，新图仍然点双连通。

由性质 5，存在包含 \(x,w\) 的简单环，则存在一个包含 \(x,(u,v)\) 的简单环。

类似地，对于边双内任意一点 \(x\) 与任意一条边 \((u,v)\)，存在一个包含 \(x,(u,v)\) 的回路。

Property 7

对于点双内任意三点 \(x,y,z\)，存在一条 \(x\rightarrow z\rightarrow y\) 的简单路径。

若存在一个包含 \(x,z\) 的简单环 \(P\) 包含 \(y\)，则成立。

否则，我们拿出一个包含 \(x,z\) 的简单环 \(P\) 和一条 \(x\) 到 \(y\) 的路径 \(Q\)，\(P,Q\) 一定存在一个不为 \(x\) 的交点 \(v\)。

假设不存在一个这样的 \(v\)，那么这就意味着 \(P\) 上其他节点到 \(y\) 的路径中，\(x\) 为必经点，则 \(x\) 为割点。

我们找到 \(y\rightarrow x\) 方向上第一个这样的 \(v'\)，那么存在一条 \(x\rightarrow z\rightarrow v'\rightarrow y\) 的一条简单路径。

对于边双内任意三点 \(x,y,z\)，存在一条 \(x\rightarrow z\rightarrow y\) 的迹。

若存在一个包含 \(x,z\) 的回路 \(P\) 包含 \(y\)，则成立。

否则，我们拿出一个包含 \(x,z\) 的回路 \(P\) 和一条 \(x\) 到 \(y\) 的路径 \(Q\)，并拿出 \(Q\) 的 \(y\rightarrow x\) 方向上第一个与 \(P\) 的交点 \(v\)，则存在一条 \(x \rightarrow z\rightarrow v\rightarrow y\) 的迹。

Property 8

对于点双内任意两点 \(x,y\) 与一条边 \(e\)，存在一条 \(x\rightarrow e\rightarrow y\) 的简单路径。

对于边双内任意两点 \(x,y\) 与一条边 \(e\)，存在一条 \(x\rightarrow e\rightarrow y\) 的迹。

结合性质 7 与性质 4 易证。