P7163 [COCI 2020/2021 #2] Svjetlo 做题记录

P7163 [COCI 2020/2021 #2] Svjetlo 做题记录

Description

https://www.luogu.com.cn/problem/P7163

有一个呈树状结构的吊灯，由 \(n\) 个灯泡组成，这些灯泡之间有 \(n-1\) 根电线连接。每个灯泡有一个按钮，能使灯泡的状态发生改变，即把打开的灯泡关闭，关闭的灯泡打开。你需要把所有的灯泡打开。

你可以选择一个序列，序列中两两相邻位置的灯泡相邻，灯泡可以在序列中出现多次。你可以依次改变序列中的灯泡的状态。求序列最短长度。

\(2 \leq n \leq 500,000\)。

Solution

很 nb 的树形 dp。

I. 状态设计

我们最终的路径有两个端点。那么子树 \(x\) 内的端点个数可能为 \(0,1,2\)。

于是设 \(f_{x,0/1},g_{x,0/1},h_{x,0/1}\) 为 \(x\) 子树内全部点亮，当前 \(x\) 是否点亮，\(x\) 子树内端点个数为 \(0/1/2\) 的最小代价。

可以看出，\(f,h\) 都会在 \(x\) 处伸出两个线头，\(g\) 会在 \(x\) 处伸出一个线头。

为了方便转移和统计答案，我们令 \(f,h\) 在 \(x\) 处伸出的线头一个在里面，一个在外面（也就是一个在 \(x\) 的某一个儿子上，另一个已经走出了 \(x\) 但还没有到达其他点），令 \(g\) 伸出的线头在外面。

起始状态：\(f_{x,a_x}=0\)，其他都设为 \(+\infty\)。

终止状态：我们找到一个初始为 \(0\) 的点 \(s\) 作为根，答案为 \(h_{s,1}\)。

下面是图片解释（小点是线头，大点是路径端点）：

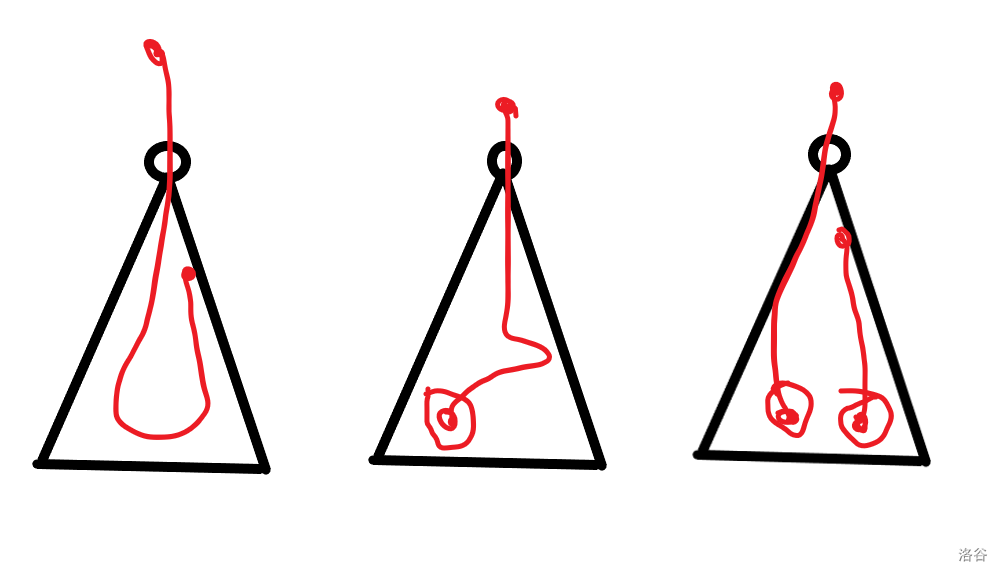
II. 转移

考虑将 \(x\) 的儿子 \(y\) 里面的路径接到 \(x\) 上。

如果要将 \(x\) 变为 \(1\)，那么若两个节点都是 \(0\)，\((x,y)\) 这条边在接续时走一个来回就可以把它们都变为 \(1\)，代价为 \(2\)；否则，接续完毕后需要再走一个来回，代价为 \(4\)。

如果要将 \(x\) 变为 \(0\)，也是同理的。

\(f\) 的转移：

\[f_{x,1}=\min(f_{x,0}+f_{y,0}+2,f_{x,1}+f_{y,1}+4) \]

\[f_{x,0}=\min(f_{x,1}+f_{y,1}+2,f_{x,0}+f_{y,0}+4) \]

\(g\) 的转移：

\[g_{x,1}=\min(g_{x,0}+f_{y,0}+2,g_{x,1}+f_{y,1}+4,f_{x,0}+g_{y,1}+1,f_{x,1}+g_{y,0}+3) \]

\[g_{x,0}=\min(g_{x,1}+f_{y,1}+2,g_{x,0}+f_{y,0}+4,f_{x,1}+g_{y,0}+1,f_{x,0}+g_{y,1}+3) \]

\(h\) 的转移：

\[h_{x,1}=\min(f_{x,0}+h_{y,0}+2,f_{x,1}+h_{y,1}+4,g_{x,0}+g_{y,0}+2,g_{x,1}+g_{y,1},h_{x,0}+f_{y,0}+2,h_{x,1}+f_{y,1}+4) \]

\[h_{x,0}=\min(f_{x,1}+h_{y,1}+2,f_{x,0}+h_{y,0}+4,g_{x,1}+g_{y,1}+2,g_{x,0}+g_{y,0},h_{x,1}+f_{y,1}+2,h_{x,0}+f_{y,0}+4) \]

画图推导可以辅助理解。注意 \(f,h\) 转移时要让一个线头留在 \(x\) 子树里面。

最后还要考虑线头就在 \(x\) 时的转移：

\[g_{x,0}\leftarrow f_{x,1}+1,g_{x,1}\leftarrow f_{x,0}+1 \]

\[h_{x,0}\leftarrow g_{x,0},h_{x,1}\leftarrow g_{x,1} \]

让 \(f\) 的子树内的线头走到 \(x\)，成为路径端点；让 \(g\) 伸出的线头退回子树内，并在 \(x\) 上加一个伸出的线头。

如果一个儿子 \(y\) 的子树内所有节点都是 \(1\)，那么不需要统计进 \(y\) 的答案，否则需要会增加不必要的代价。

时间复杂度 \(O(n)\)。

void dfs2(int x,int pr){
    f[x][w[x]]=0;
    int F[2],G[2],H[2];
    for(int i=head[x];i;i=edge[i].nxt){
        int t=edge[i].to;
        if(t==pr||siz[t]==cnt[t]) continue;
        dfs2(t,x);
        F[0]=f[x][0],F[1]=f[x][1],G[0]=g[x][0],G[1]=g[x][1],H[0]=h[x][0],H[1]=h[x][1];
        f[x][0]=min({F[0]+f[t][1]+4,F[1]+f[t][0]+2});
        f[x][1]=min({F[1]+f[t][1]+4,F[0]+f[t][0]+2});
        g[x][0]=min({F[0]+g[t][0]+3,F[1]+g[t][1]+1,G[0]+f[t][1]+4,G[1]+f[t][0]+2});
        g[x][1]=min({F[0]+g[t][1]+1,F[1]+g[t][0]+3,G[0]+f[t][0]+2,G[1]+f[t][1]+4});
        h[x][0]=min({F[0]+h[t][1]+4,F[1]+h[t][0]+2,H[0]+f[t][1]+4,
                     H[1]+f[t][0]+2,G[0]+g[t][1],G[1]+g[t][0]+2});
        h[x][1]=min({F[0]+h[t][0]+2,F[1]+h[t][1]+4,H[0]+f[t][0]+2,
                     H[1]+f[t][1]+4,G[1]+g[t][1],G[0]+g[t][0]+2});
    }
    g[x][0]=min(g[x][0],f[x][1]+1);
    g[x][1]=min(g[x][1],f[x][0]+1);
    h[x][0]=min(h[x][0],g[x][0]);
    h[x][1]=min(h[x][1],g[x][1]);
}