20250205 省选模拟赛 T3

20250205 省选模拟赛 T3

Description

设计一个 \(n\times n\) 的 01 矩阵，使得从 \((1,1)\) 走到 \((n,n)\) 且只能向右或下走且只经过为 \(1\) 的格子的方案数为 \(X\)。

\(n \leq 24\) 时得满分。\(X \leq 10^9\)。

Solution

基于 \(2\) 进制的构造方法

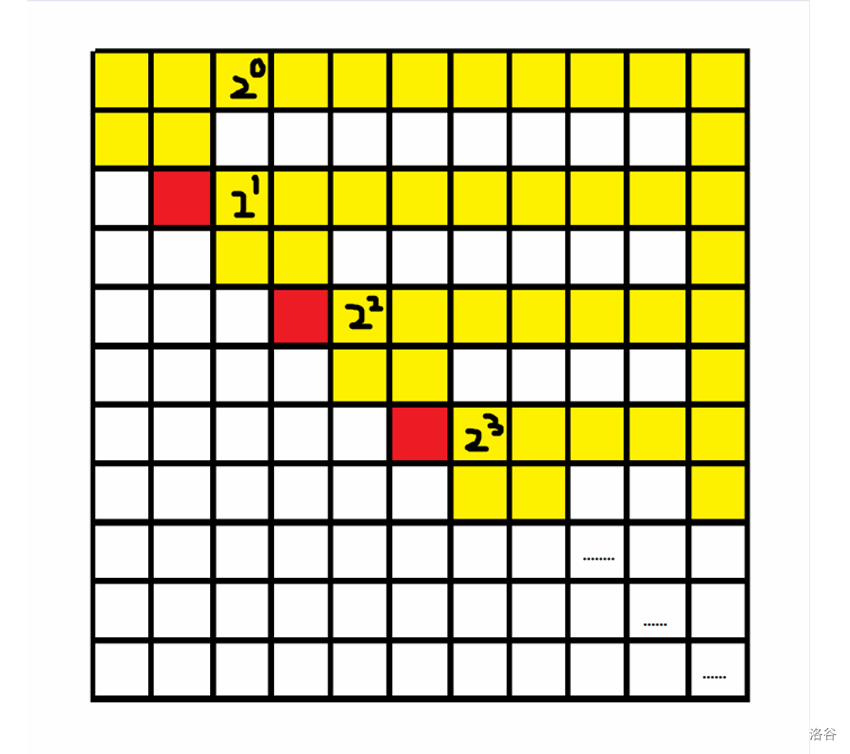
我们称从左上到右下的 \(2\times 2\) 的方块为 “基块”，延伸至右侧的长条为 “导线”。最右侧的导线占据了 \((1,n)\) 至 \((n,n)\)。

从一个红色方块走到右下方的红色方块，方案数为 \(2\)。从 \(0\) 从左上到右下标号，走到第 \(i\) 个方格的走法有 \(2^i\) 种。

构造方法为，如果 \(X\) 在二进制下第 \(i\) 位为 \(1\)，我们就从第 \(i\) 个红色方块向右拉一条导线。

基于 \(6\) 进制的构造方法

将基块改为 \(3\times 3\)，那么从基块的左上角走到右下角方案数为 \(6\)。

在 \(6\) 进制下，如果 \(X\) 的第 \(i\) 位有值，我们就向下或向右拉一条导线。

此时需要图中蓝色和绿色的 “位块” 来处理每一位的值，对 \(1,2,3,4,5\) 分别构造。

基于 \(20\) 进制的构造方法

同上，我们将基块改为 \(4\times 4\)，走完一个基块的方案数变为 \(20\)。

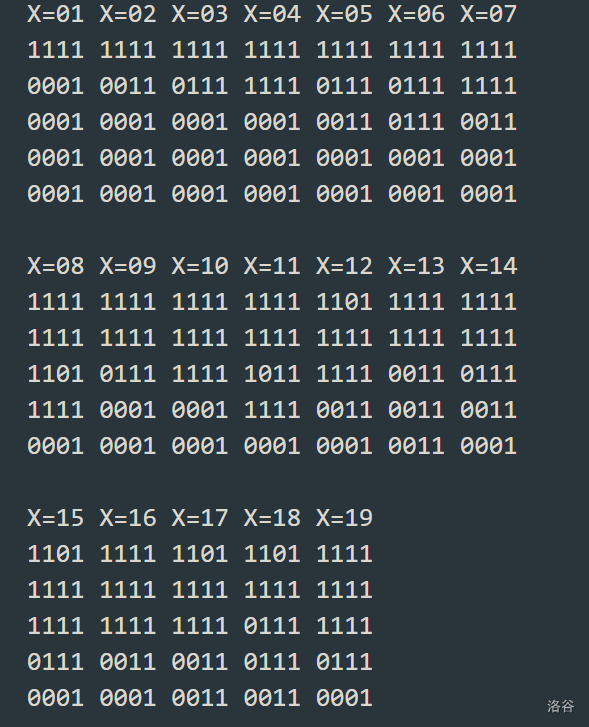
此时我们需要 \(4 \times 5\) 的位块，它们需要满足最右侧全部为 \(1\)，以接在导线上。

使用 dfs 进行枚举：

void dfs(int x,int y){
    if(!x) return Check();
    if(!y) return dfs(x-1,m);
    if(y!=m&&(!(x==1&&y==1))){
        a[x][y]=0; dfs(x,y-1);
        if(ok) return;
    }
    a[x][y]=1; dfs(x,y-1);
}

如果再像上面一样构造，\(n\) 至少为 \(25\)。考虑对最高位进行优化。

最高位的位块我们改为 \(3 \times 6\)，这样可以同时利用两条导线，省掉一行一列。

由于 \(X\leq 10^9\)，只需要处理 \(1\sim 15\)。它们需要满足最下方和最右方都为 \(1\)。

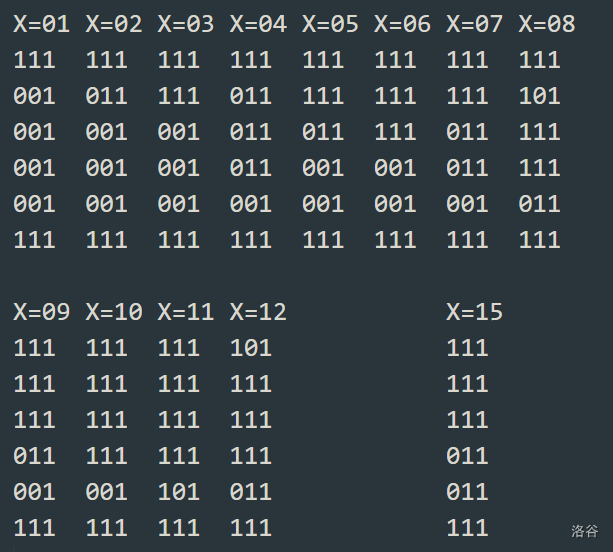
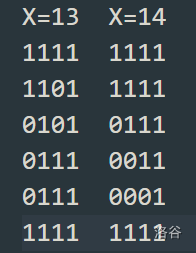
但我们无法构造出 \(13,14\) 的位块。考虑换用 \(4\times 6\)：

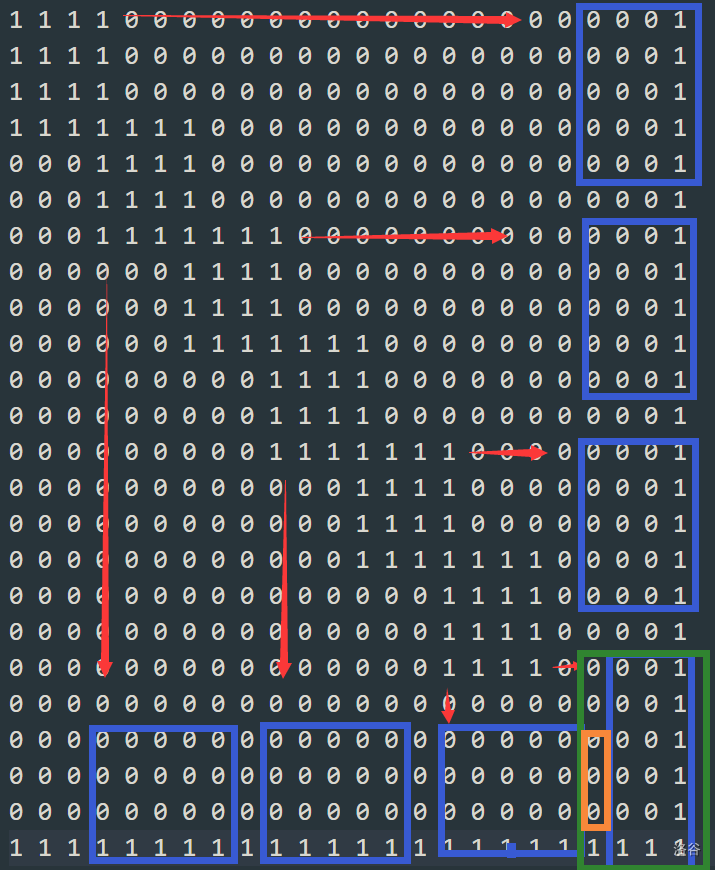
绿色部分为新换用的位块。为了避免与左侧位块 “粘连”，橙色区域必须为 \(0\)。

int val1[23][8][8],val2[23][8][8];
int f[8][8],X,c[8];
bool ok;

void Check1(int k){
    memset(f,0,sizeof(f));
    f[0][0]=1;
    for(int i=0;i<=4;i++){
        for(int j=0;j<=3;j++){
            if(i<4&&val1[k][i+1][j]) f[i+1][j]+=f[i][j];
            if(j<3&&val1[k][i][j+1]) f[i][j+1]+=f[i][j];
        }
    }
    if(f[4][3]==k) ok=1;
}

void dfs1(int x,int y,int k){
    if(x<0) return Check1(k);
    if(y<0) return dfs1(x-1,3,k);
    if(y!=3&&(!(x==0&&y==0))){
        val1[k][x][y]=0;
        dfs1(x,y-1,k);
        if(ok) return;
    }
    val1[k][x][y]=1;
    dfs1(x,y-1,k);
}

void Check2(int k){
    memset(f,0,sizeof(f));
    f[0][0]=1;
    for(int i=0;i<=5;i++){
        for(int j=0;j<=2;j++){
            if(i<5&&val2[k][i+1][j]) f[i+1][j]+=f[i][j];
            if(j<2&&val2[k][i][j+1]) f[i][j+1]+=f[i][j];
        }
    }
    if(f[5][2]==k) ok=1;
}

void dfs2(int x,int y,int k){
    if(x<0) return Check2(k);
    if(y<0) return dfs2(x-1,2,k);
    if(y!=2&&x!=5&&(!(x==0&&y==0))){
        val2[k][x][y]=0;
        dfs2(x,y-1,k);
        if(ok) return;
    }
    val2[k][x][y]=1; dfs2(x,y-1,k);
}

void Check3(int k){
    memset(f,0,sizeof(f));
    f[0][0]=1;
    for(int i=0;i<=5;i++){
        for(int j=0;j<=3;j++){
            if(i<5&&val2[k][i+1][j]) f[i+1][j]+=f[i][j];
            if(j<3&&val2[k][i][j+1]) f[i][j+1]+=f[i][j];
        }
    }
    if(f[5][3]==k) ok=1;
}

void dfs3(int x,int y,int k){
    if(x<0) return Check3(k);
    if(y<0) return dfs3(x-1,3,k);
    if(y!=3&&x!=5&&(!(x==0&&y==0))){
        val2[k][x][y]=0;
        dfs3(x,y-1,k);
        if(ok) return;
    }
    if(!(y==0&&x<5&&x>=2)){
        val2[k][x][y]=1;
        dfs3(x,y-1,k);
        if(ok) return;
    }
}

void Init(){
    for(int i=1;i<=19;i++){
        ok=0;
        dfs1(4,3,i);
    }
    for(int i=1;i<=15;i++){
        if(i==13||i==14) continue;
        ok=0;
        dfs2(5,2,i);
        
    }
    ok=0; dfs3(5,3,13);
    ok=0; dfs3(5,3,14);
}

int ans[26][26];

signed main(){
    FileIO();
    Init();
    read(X);
    for(int i=1;i<=7;i++){
        c[i]=X%20;
        X/=20;
        // printf("C[%d]=%d\n",i,c[i]);
    }
    for(int i=1;i<=24;i++) ans[i][24]=ans[24][i]=1;
    for(int i=1,x=1;i<=6;i++,x+=3){
        for(int j=0;j<=3;j++){
            for(int k=0;k<=3;k++)
                ans[x+j][x+k]=1;
        }
    }
    for(int i=1,x=1;i<=7;i++,x+=3){
        // printf("I=%d,X=%d\n",i,x);
        if(!c[i]) continue;
        if(i%2==0){
            for(int j=x;j<=24;j++) ans[j][x]=1;
            for(int j=0;j<=3;j++){
                for(int k=0;k<=4;k++)
                    ans[24-(3-j)][x+k]=val1[c[i]][k][j];
            }
        }
        else if(i<=6){
            for(int j=x;j<=24;j++) ans[x][j]=1;
            for(int j=0;j<=4;j++){
                for(int k=0;k<=3;k++)
                    ans[x+j][24-(3-k)]=val1[c[i]][j][k];
            }
        }
        else if(c[i]==13||c[i]==14){
            for(int j=x;j<=24;j++) ans[x][j]=1;
            for(int j=0;j<=5;j++){
                for(int k=0;k<=3;k++)
                    ans[x+j][24-(3-k)]=val2[c[i]][j][k];
            }
        }
        else{
            for(int j=x;j<=24;j++) ans[x][j]=1;
            for(int j=0;j<=5;j++){
                for(int k=0;k<=2;k++)
                    ans[x+j][24-(2-k)]=val2[c[i]][j][k];
            }
        }
    }
    puts("24");
    for(int i=1;i<=24;i++){
        for(int j=1;j<=24;j++){
            putchar(ans[i][j]+'0');
            putchar(' ');
        }
        puts("");
    }
    return 0;
}